Exercícios de Centro de Massa e Momento de Inércia - Lista de Exercícios Resolvida
Questão 1
Encontre o momento de inércia em relação ao eixo de uma casca fina de densidade constante cortada do cone , pelo cilindro circular
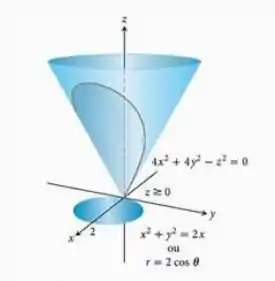
Questão 2
Encontre o centro de massa, o momento de inércia e o raio de rotação em relação ao eixo de uma casca fina de densidade constante cortada do cone pelo planos e
Ver solução completaQuestão 3
Sabendo que o centro de massa de uma superfície é definido por
Onde é a massa total de e é a densidade em cada ponto , calcule o centro de massa das seguintes superfícies com densidade constante.
- tem representação paramétrica , .
- é a parte da superfície cônica compreendida entre os planos e
Questão 4
O centroide de um superfície é definido por
Encontre o centroide da superfície na porção do paraboloide
Abaixo do plano .
Ver solução completaQuestão 5
Calcule a massa da superfície limitada pelos planos e , onde a densidade de massa é .
Ver solução completaQuestão 6
Calcule a massa da superfície definida como sendo a parte da superfície satisfazendo e densidade de massa é .
Ver solução completaQuestão 8
Calcule a massa de com densidade superficial de massa , onde é o hemisfério da esfera tal que e .
Ver solução completaQuestão 9
22) Calcule o centro de massa da superfície homogênea, parte da superfície cônica , compreendida entre os planos e .
Ver solução completaQuestão 10
21) Calcule o momento de inércia da superfície esférica de raio , homogênea, de massa , em torno de qualquer diâmetro.
Ver solução completaQuestão 11
19) Uma lâmina tem a forma de um hemisfério de raio de raio . Calcule o momento de inércia dessa lâmina em relação a um eixo que passa pelo polo e é perpendicular ao plano que delimita o hemisfério. Considere a densidade no ponto da lâmina proporcional à distância desse ponto ao plano que delimita o hemisfério.
Ver solução completaQuestão 12
16) Determine o momento de inércia em relação ao eixo da superfície , limitada por e , sendo a densidade
Ver solução completaQuestão 15
Determine a massa da superfície dada por limitada por , sabendo que a densidade é dada por .
Ver solução completaQuestão 16
18) Calcule o momento de inércia da superfície homogênea, de massa , de equação , , com , em torno do eixo .
Ver solução completa