Fazer um esboço do gráfico de , determinando:
. Os extremos relativos de ;
. Os pontos de inflexão do gráfico de ;
. Os intervalos onde é crescente e aqueles nos quais é decrescente;
. Onde o gráfico é côncavo para cima e onde é côncavo para baixo;
Da função
Passo 1
Legal gente, sem pânico! Temos milhões de coisas pra calcularmos, então vamos ser organizados e dividir tudo em pequenos passos de cada vez. A primeira coisa que a questão nos pede, é que determinemos os extremos relativos de f. Para isso, temos que:
- Fazer a primeira derivada e igualar a 0 para achar um c
- Fazer a segunda derivada e realizar um teste para determinamos se é um extremo ou mínimo relativo.
Então, nossa função é dada por:
Derivando e igualando a 0, temos que:
Resolvendo essa equação, temos que a raíz é:
Então temos 1 C. Vamo aos testes! A segunda derivada da função é igual a:
Aplicando , temos que:
-p/ :
Para esse caso, pode-se afirmar que não existem nem máximos ou mínimos relativos.
Passo 2
Ufa, primeira parte já foi! Para a segunda parte, precisamos definir o nosso ponto de inflexão. Resumindo, vamos derivar 3 vezes e achar esses pontos? PREPARADOS? SIMBORA!
Neste ponto, igualamos a 0 e temos nossos primeiros candidatos a pontos de inflexão.
Agora vamos derivar pela terceira vez, se essa derivada for diferente de 0, os nossos candidatos a pontos de inflexão são realmente pontos de inflexão.
Logo, nosso ponto (-2,2) é um ponto de inflexão.
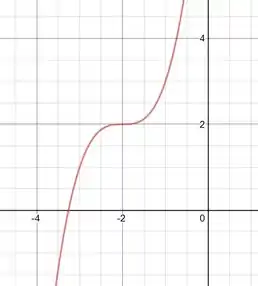
Passo 3
E vamos seguindo o rumo galera! Para determinamos a região aonde a nossa curva cresce e decresce, é bem simples. Derivamos uma vez, achamos os 0 e comparamos os intervalos dos 0. Como assim? Vamos lá.
Para a nossa função, temos que a primeira derivada é igual a
As raízes dessa equação correspondem somente a .
Então, analisando antes de -2, nossa função fica positiva, indicando crescimento da função. Analisando depois de -2, também nossa função fica positiva, indicando crescimento da função.
Passo 4
Como só temos 1 ponto de inflexão, só temos 1 regiao côncava e outra convexa, respectivamente indo de e .
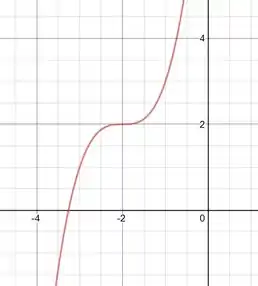
Resposta
Não existem máximos ou mínimos relativos
Ponto de inflexão
Crescente para e para
Côncava para e convexa para