Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 1.2 - Ex. 2.f
Estude o sinal da expressão.
Passo 1
Para estudar o sinal da expressão vamos analisar as duas expressões separadamente:
Para temos o seguinte esquema:
Vamos analisar os sinais dessa expressão na direita e na esquerda do ponto :
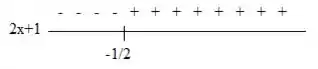
A expressão assume valores negativos quando e assume valores positivos quando .
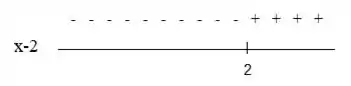
Para temos:
Aqui vamos analisar os sinais dessa expressão na direita e na esquerda do ponto :
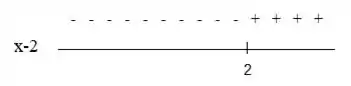
Aqui a expressão assume valores negativos quando e assume valores positivos quando .
Passo 2
Vamos analisar agora as três situações, quando a expressão toda é maior que zero, menor e igual a zero:
Para maior que zero temos:
Para menos que zero:
E para igual a zero:
Passo 3
Vamos lá, para resolver a primeira inequação vamos analisar as duas imagens que achamos no passo anterior:
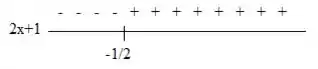
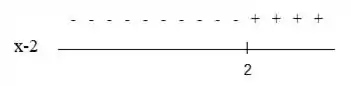
Temos que quando as duas expressões forem ambos positivos ou ambos negativos, ou seja, possuírem o mesmo sinal, analisando as duas imagens vemos que isso acontece quando:
ou
Passo 4
Para resolver a segunda inequação vamos fazer a mesma análise:
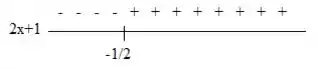
Temos que quando as duas expressões tiverem sinais opostos, analisando as duas imagens vemos que isso acontece quando:
Passo 5
Agora vamos resolver a equação igual a zero, temos que analisar a seguinte equação:
Para ela ser zero precisamos que uma das expressões seja igual a zero, assim temos:
Resposta
para ou
para
para ou