Para o mapa de contorno dado, desenhe as curvas de maior crescimento em e em .
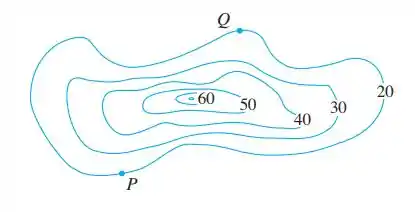
Passo 1
O Teorema 15 da teoria nos disse que o vetor gradiente indica a direção de maior crescimento da função . Mas a gente também sabe que o vetor gradiente é ortogonal às superfícies de nível de . Como queremos a curva de maior crescimento, a ideia ver ser “entrarmos” ortoganal em todas as curvas, olha só:
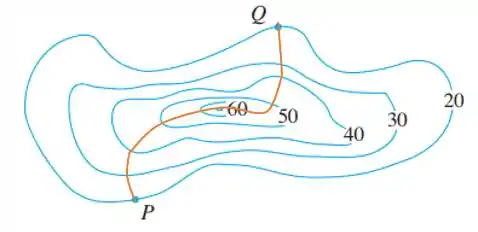
Repare que nesse exemplo entramos perpendicular em todas as superfícies de nível. Temos infinitas curvas que atendem ao pedido do enunciado.
Resposta
Ei, a resposta está no passo a passo :)