Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 1.1 - Ex. 5
Seja , com , e . Desenhe a imagem de .
Passo 1
Vamos lá, aqui a gente tá saindo do e indo para o . É como se tivéssemos:
Veja que as condições de nos dão três pontos (em ). Como assim? Olha só:
Se , e os três pontos limitantes aqui são:
Certo? Vamos seguir então...
Passo 2
Aplicando a transformação nesses três pontos, encontramos os limitantes da imagem, ou seja os vértices da figura que vai formar. Os pontos transformados ficam:
E aí o desenho da imagem é esse:
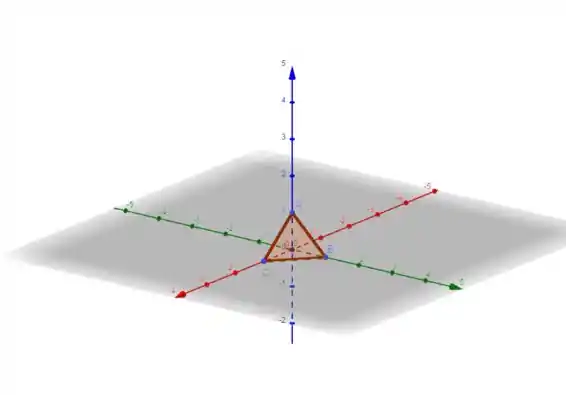
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Seja f a transformação de R 2 em R 3 dada por x , y , z = ( u + v , u , v ) . Mostre que f transforma o plano u v no plano x - y - z = 0 .
2. a. Encontre uma parametrização para a superfície obtida girando-se o circulo x - a 2 + z 2 = r 2,0ra , torno do eixo z. Esta superfície é chamada de toroB . Encontre um vetor normal a essa superfíc
1 . Seja S uma superfície parametrizada por φ u , v = v cos u ,v s e nu , 1 - v 2 0u2 π v ≥ 0 Identifique esta superfície. Esta superfície é regular ? Trace as curvas na superfice S. Definidas por φ
3. Considere as superfícies S 1 e S 2 parametrizadas por φ 1 u , v = u , v , 0 φ 2 u , v = u 3 , v 3 , 0 u , v ∈ R 2 Respectivamente Mostre que S1 e S2 são o plano XYMostre que S1 é regular e que S3 n