Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.1 - Ex. 45

Um tanque cheio de água tem a forma de um sólido de revolução formado quando a região limitada pela curva y = e - x , pelos eixos coordenados e pela reta x = 4 gira em torno do eixo x . Ache o trabalho realizado ao bombear toda a água para a borda do tanque. A distância é medida em metros. Tome o eixo x vertical e orientado para baixo.

Passo 1

O trabalho realizado para levantar uma massa m de água uma altura h é dado por W = m g h , sendo g o valor da aceleração da gravidade. Podemos separar o volume do tanque em pequenos “discos” de água com altura infinitesimal d x , e então encontrar o trabalho infinitesimal d W necessário para levantar cada “disco” de abscissa x até a borda do tanque. O nosso trabalho W será obtido então a partir da integração de d W .

Passo 2

Primeiro devemos tentar esboçar o formato do nosso tanque. Colocamos o eixo x virado para baixo e o eixo y para a direita, com a origem no topo do tanque em seu centro. Na base do tanque temos x = 4 e o raio é y 4 = e - 4 . No topo temos x = 0 e o raio é y 0 = e 0 = 1 .

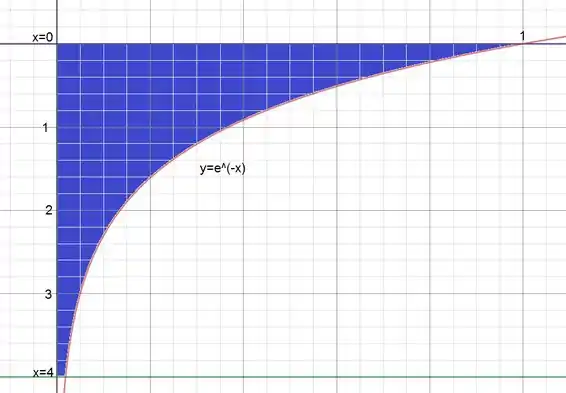
Cada disco de água terá então um volume d V = π e - x 2 d x = π e - 2 x d x . Se a densidade volumétrica da água for ρ , a massa de cada disco de abscissa x é então d m = π ρ e - 2 x d x . Além disso, o disco deverá ser levantado de uma altura x , então:

d W = d m ⋅ g ⋅ h = π ρ e - 2 x d x ⋅ g ⋅ x = π ρ g   x e - 2 x d x

Passo 3

Agora devemos integrar d W , indo de x = 0   a x = 4 . Para calcular ∫ x e - 2 x d x , usamos a integração por partes. Escolhemos u = x e d v = e - 2 x d x . Isso nos dá:

d u = d x ; v = - 1 2 e - 2 x

Então:

∫ u   d v = u v - ∫ v   d u ⇒ ∫ x e - 2 x d x = - x 2 e - 2 x - ∫ - 1 2 e - 2 x d x = - x 2 e - 2 x - 1 4 e - 2 x + C  

Agora podemos integrar d W :

∫ 0 4 d W = ∫ 0 4 π ρ g   x e - 2 x d x = π ρ g - x 2 e - 2 x - 1 4 e - 2 x 0 4 =

π ρ g - 4 2 e - 8 - 1 4 e - 8 - 0 - 1 4 e 0 = π ρ g 7 4 e - 8 + 1 4 = π ρ g 1 + 7 e - 8 4

Resposta

d W = π ρ g 1 + 7 e - 8 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a fórmula: ∫ f - 1 x d x = x f - 1 x - ∫ f y d y , sendo y = f - 1 ( x ) Expresse suas respostas em termos de x:69 - ∫ sec - 1 ⁡ x d x
Use a integração por partes para estabelecer a fórmula de redução:64 - ∫ ( ln ⁡ x ) n d x = x ( ln ⁡ x ) n - n ∫ ln ⁡ x n - 1
As Equações 4 e 5 dão fórmulas diferentes para a integral de cos - 1 ⁡ x 72 – ∫ tg - 1 ⁡ xd x = x t g - 1 x - ln ⁡ sec ⁡ t g - 1 x + c ∫ tg - 1 ⁡ xd x = x t g - 1 x - l n 1 + x 2 + c As duas integraçõ
Use a fórmula: ∫ f - 1 x d x = x f - 1 x - ∫ f y d y , sendo y = f - 1 ( x ) Expresse suas respostas em termos de x:68 - ∫ t g - 1 xd x
Use a integração por partes para estabelecer a fórmula de redução:61 - ∫ x n c o s xd x = x n s e n x - n ∫ x n - 1 s e nxd x