Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.7 - Ex. 19
Use a integral tripla para determinar o volume do sólido dado.
O sólido delimitado pelo cilindro e pelos planos e
Passo 1
E aí, pessoal! Tudo bacana?
A questão aqui pede que a gente calcule o volume do sólido delimitado pelo cilindro
e pelos planos
e
Para calcular o volume de um sólido, precisamos calcular a integral:
Onde é a região de integração do sólido no plano e
Então, o que falta para calcularmos nossa integral tripla são os limites de integração para cada uma das variáveis, e isso a gente consegue entendendo a descrição da região que o enunciado nos deu.
Com isso em mãos, é só a gente calcular a integral tripla de forma iterada, onde começamos pela “de dentro”, até chegarmos na última integral de fora. Assim, vamos ter o volume do sólido que procuramos.
Vamos, então?
Passo 2
Vamos começar achando nosso limite de integração.
Podemos achar de cara a variação de isolando-o na equação do plano
Como temos como limitantes da região o plano , sabemos que zero é o valor mínimo para , então ficamos com:
Para as outras duas variáveis, vamos ter que analizar e a intersecção do plano com , essa intersecção é
Olhando no plano temos
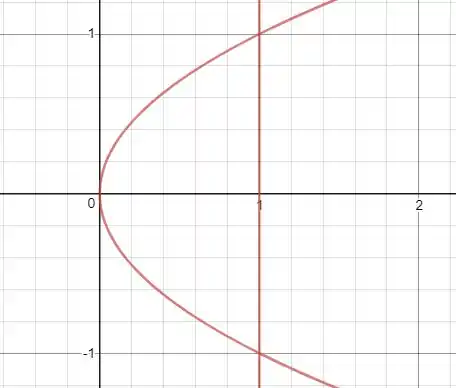
Reta e curva
Então a variação de vai ser
e a de , quando , na intersecção , ou seja, o intervalo é
Passo 3
Montando nossa integral, temos:
Sempre colocamos as integrais com limites que dependem de variáveis para dentro, para facilitar nosso cálculo. Vamos começar integrando em e aplicando os limites de integração:
Agora calculando em função de :
Aplicando os limites de integração:
Agora integramos nossa integral que restou:
Calculando seus limites:
Simplificando:
Chegamos no volume que procurávamos!