Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.9 - Ex. 10
Use o teorema do divergente para calcular a integral de superfície ; ou seja, calcule o fluxo de através de .
é a superfície do tetraedro limitado pelos planos coordenados e o plano
onde , e são números positivos
Passo 1
Faala, galera!
Nessa questão, temos que calcular uma integral de superfície usando o teorema do divergente:
Onde é o sólido delimitado por .
Isso quer dizer em vez de calcularmos a integral de superfície, vamos calcular a integral tripla.
Então começamos calculando o divergente de :
No nosso caso:
Então:
Depois, vamos definir quem é , e definir a integral tripla. No final, vamos calcular ela.
Passo 2
Começando pelo divergente.
Derivando em função de , com constantes:
Derivando em função de , com constantes:
Derivando em função de , com constantes:
Então:
Passo 3
Agora vamos ver o sólido .
Como , o plano
Vai cortar os três eixos na parte positiva, e fica assim:
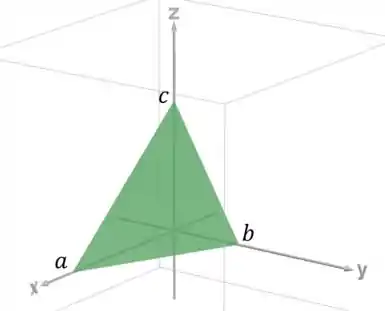
E nosso sólido é esse tetraedro abaixo do plano.
Podemos reescrever:
Então:
Daí, definimos:
Passo 4
Para os limites de e , vamos ver a projeção desse sólido no plano :
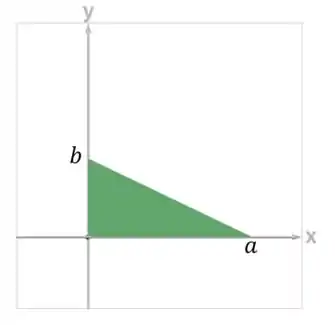
O sólido é limitado pela reta que é a interseção do plano com :
Ou seja:
E
Percebe que como os limites de dependem de , e os de dependem de , temos que integrar primeiro em função de , depois de e por último de .
Então:
Passo 5
Agora vamos calcular essa integral, de dentro pra fora:
Esse pode sair das duas primeiras integrais, já que depende só de :
Integrando em função de , com constantes:
Vamos colocar o pra fora da integral:
Passo 6
Integrando em função de , com constantes:
Colocando em evidência e substituindo:
Simplificando o :
Colocando em evidência:
Podemos tirar e da integral por serem constantes:
Passo 7
Antes de integrar em função de , abrir os produtos:
E distributiva:
Agora podemos integrar:
Simplificando:
Colocando em evidência: