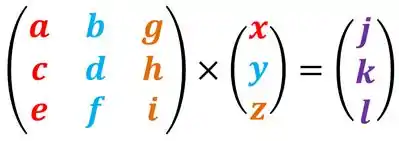Introdução aos Sistemas Lineares
Produzido por Marcelo LuizTeoria
Equações lineares
Faaalaa meus queridos, tudo bem? Hoje é o dia de tu sair daqui sabendo sobre sistemas lineares. Mas antes de irmos direto para essa parte, vamos dar uma relembradinha em equações.
As equações nada mais são do que uma solução para os nossos problemas (e não o contrário haha). É por meio dela que podemos encontrar o valor de algo que queremos saber.

Por exemplo, tu tirou um na primeira prova de Bases hehe, e quer saber que nota você precisa tirar na segunda prova pra passar com média . Aí você pensa:
Fazendo isso na verdade você está usando uma equaçãozinha, mais especificamente essa aqui:Onde o é o valor que você quer saber, ele é chamado de incógnita. Nesse caso, temos apenas uma, mas podemos ter várias ( ).Exemplos de equações:
Essa é a ideia, só mais uma coisa, quando falamos de sistemas lineares, vamos usar equações lineares. Para que uma equação seja linear, duas coisas têm que acontecer:
- As incógnitas só podem ter expoente igual a 1, ou seja, não pode ter expoentes ao quadrado, ou ao cubo ...
- Não ter duas ou mais incógnitas se multiplicando.
Ou seja,
Não são equações lineares, a primeira tem e a segunda tem .
Sistemas lineares
Quando falamos de sistemas lineares estamos falando de um conjunto de equações, com mais de uma incógnita. E a solução do sistema, satisfaz simultaneamente todas as equações. E para representar um sistema, colocamos as equações dentro de uma chave ““. Por exemplo:
É um sistema linear de duas equações e duas incógnitas.
É um sistema linear de 3 equações e 3 incógnitas. Nos sistemas, os termos que não possuem nenhuma incógnita, são chamados termos independentes. Quando todos os termos independentes são iguais, dizemos que temos um sistema linear homogêneo. Exemplo:
É um sistema linear homogêneo de duas equações.
Representação matricial de um sistema
Da uma olhada nesse sisteminha aqui:
E se eu te falar que podemos escrever ele assim:
Siiim, nós PODEMOS escrever um sistema em forma de matriz.
A primeira matriz é feita dos valores (ou coeficientes) que multiplica cada uma das incógnitas, mas cuidado:
Assim, na primeira coluna colocamos os coeficientes de , na segunda de , na terceira de e na quarta de . E cada equação do sistema tem a sua linha. Depois de montar essa equação, temos multiplicado a ela uma matriz coluna com as variáveis. É importante que ela esteja na ordem que você montou sua matriz dos coeficientes.
Como nesse caso montamos a primeira coluna com os coeficientes da variável , a primeira variável a ser colocada é o . Depois igualamos a uma matriz com os termos independentes.
E pronto, aí está a representação matricial do seu sistema.
Agora, vamos para os Exerciiiciossss
Sistemas lineares
Representação matricial de um sistema
Exercícios Resolvidos
Exercício Resolvido #1
DANTE, Luiz Roberto. Matemática- contexto e aplicações. ED. Renovada. São Paulo, SP: ática, 2010. pp.145
Identifique com a letra A as equações lineares e com a letra B as equações que não são lineares:
Passo 1
Para fazer esse exercício, vamos nos lembrar de que nas equações lineares. Tem duas coisas tem que acontecer:
- As incógnitas só podem ter expoente igual a 1, ou seja , não pode ter expoentes ao quadrado, ou ao cubo ...
- Não ter duas ou mais incógnitas se multiplicando.
Agora, vamos analisar cada uma.
.
Passo 2
Podemos ver, que tanto o x como o y , estão com o expoente 1. E não temos incógnitas se multiplicando, assim temos uma equação linear.
Não temos incógnitas se multiplicando, mas temos uma ao quadrado (). Por isso, não temos uma equação linear
Nesse caso, tanto x como y, estão com o expoente igual a um, porém eles estão se multiplicando, por isso não temos uma equação linear.
Agora, temos três incógnitas (x, y e z), e todas estão com o expoente igual a 1. E nenhuma está se multiplicando, por isso é um sistema linear.
Novamente temos três incógnitas ( e ), nenhuma está se multiplicando e todas possuem expoente 1. Assim é uma equação linear.
Resposta
Exercício Resolvido #2
DANTE, Luiz Roberto. Matemática- contexto e aplicações. ED. Renovada. São Paulo, SP: ática, 2010. pp.145
Verifique se o par ordenado:
- é uma solução da equação linear
- é uma solução da equação linear
Passo 1
Em um par ordenado, temos :
A primeira posição, temos o valor correspondente a x, e na segunda o correspondente a y.
Para descobrir se um par ordenado satisfaz uma equação, basta substituirmos o valor dado na equação.
Passo 2
- Nesse caso o nosso par ordenado é :
- Nosso par ordenado é
6 é o valor de x, e 2 é o valor de y. Para descobrir se satisfaz a equação , vamos substituir os valores do nosso par ordenado:
Assim, vimos que o par ordenado satisfaz a equação linear.
Passo 3
Onde e
Vamos substituir esses valores na nossa equação, para descobrir se satisfaz :
Opaa, acabamos de achar uma informação falsa, na verdade
Assim , o par ordenado não satisfaz a equação.
Resposta
- Sim
- Não
Exercício Resolvido #3
DANTE, Luiz Roberto. Matemática- contexto e aplicações. ED. Renovada. São Paulo, SP: ática, 2010. pp.145
Verifique se o terno ordenado:
- é uma solução para a equação linear
- é uma solução para a equação linear
Passo 1
Uma terna ordenada é :
Onde o valor da primeira posição, corresponde ao valor de x, a segunda ao de y e a terceira posição é o valor de z.
Para descobrir de ele satisfaz uma equação, basta substituirmos os valores da nossa terna.
Passo 2
(a) Nossa terna é :
Com isso temos que , e
Vamos substituir na nossa equação para descobrir se é solução:
Assim , a terna satisfaz a equação.
Passo 3
(b) Vamos conferir, agora, a:
Substituindo na equação:
Opa, então, ela satisfaz a equação, sendo, então, uma solução! 😊
Resposta
- Sim
- Sim
Exercício Resolvido #4
DANTE, Luiz Roberto. Matemática- contexto e aplicações. ED. Renovada. São Paulo, SP: ática, 2010. pp.146
Verifique se :
é uma solução do sistema
Passo 1
Para que a terna seja solução do sistema, é necessário que satisfaça TODAS as equações que temos.
Assim, vamos substituir em cada uma e ver se ela satisfaz a equação.
Temos :
, e
Vamos jogar esses valores nas equações.
Passo 2
Primeira equação :
Vamos jogar os valores da nossa terna :
Achamos algo errado, na verdade temos que
Assim a terna não satisfaz a primeira equação, e por consequência não é solução do nosso sistema.
Resposta
Não
Exercício Resolvido #5
DANTE, Luiz Roberto. Matemática- contexto e aplicações. ED. Renovada. São Paulo, SP: ática, 2010. pp.146
Verifique se :
é uma solução do sistema
Passo 1
Para que um par ordenado seja solução de um sistema, ele tem que satisfazer TODAS as equações.
Assim, vamos substituir os valores nas duas equações que temos e veremos se é solução do nosso sistema.
Nesse caso, nosso par ordenado é :
Assim, e
Passo 2
Primeira equação:
Vamos substituir os valores do par ordenado:
Assim, vimos que ele é solução da primeira equação. Vamos testar à segunda.
Passo 3
Segunda equação:
Vamos substituir os valores do par ordenado:
Dessa forma, temos de que o par ordenado satisfaz as duas equações. Ou seja, ele é solução do sistema.
Resposta
Sim
Exercício Resolvido #6
DANTE, Luiz Roberto. Matemática- contexto e aplicações. ED. Renovada. São Paulo, SP: ática, 2010. pp.146
Verifique se :
é uma solução do sistema
Passo 1
Para que um par ordenado seja solução de um sistema, ele tem que satisfazer TODAS as equações.
Assim, vamos substituir os valores nas três equações que temos e veremos se é solução do nosso sistema.
Nesse caso, nosso par ordenado é :
Assim, e
Vamos colocar esses valores nas nossas equações.
Passo 2
Primeira equação:
Substituindo os valores :
Assim o par satisfaz a primeira equação do nosso sistema.
Passo 3
Segunda equação:
Substituindo :
Logo, também satisfaz a segunda equação.
Passo 4
Terceira equação :
Substituindo os valores do nosso par ordenado:
Acabamos de achar um erro, assim o par ordenado não satisfaz a terceira equação. E por isso não satisfaz o nosso sistema.
Resposta
Não
Exercício Resolvido #7
Elaboração Própria
Escreva o seguinte sistema na sua forma matricial :
Passo 1
Para colocarmos uma matriz na forma matricial, primeiro vamos fazer uma matriz com os coeficientes das incógnitas:

A primeira coluna é os coeficientes de x, e a segunda os de y.
Passo 2
Agora, vamos multiplicar nossa matriz por uma matriz coluna com as incógnitas, a primeira incógnita é a mesma da primeira coluna e a segunda é a mesma da segunda coluna:

Passo 3
Agora é só igualar á uma matriz coluna com os termos independentes (sem estar acompanhado com nenhuma incógnita)

Pronto, essa é a nossa forma matricial.
Resposta
Exercício Resolvido #8
Elaboração Própria
Escreva o seguinte sistema na sua forma matricial :
Passo 1
Para fazer a forma matricial, vamos montar nossa matriz com os coeficientes das incógnitas :
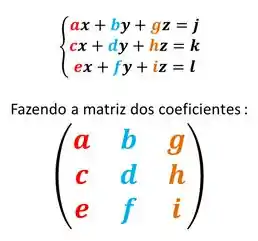
Passo 2
Agora, vamos multiplicar por uma matriz coluna das incógnitas, com a mesma ordem que formamos as colunas da matriz dos coeficientes:

Passo 3
Agora, é só igualar essa multiplicação a uma matriz coluna com os termos independentes :