Resolução de sistemas lineares com 2 e 3 incógnitas

Teoria

Sistemas com duas incógnitas

E aí minha gente! Já vimos o que é um sistema linear com duas incógnitas, um exemplo é:

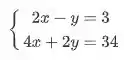
Mas como que encontramos o resultado desse sistema? Hehe é isso que vamos ver Existem vários métodos para resolver, os mais usados são :

Método da adição
Método da Substituição

Então, vamos aprender essas duas.

Método da adição

A ideia vai ser a gente somar as equações do nosso sistema, e quando fazemos essa soma, uma das incógnitas vai sumir (ou zerar). MAAAS COMOO???

Ai que surge a gambiarra hehe, nós vamos multiplicar uma das equações por um número estratégico, esse número vai nos ajudar a zerar uma incógnita quando fizermos a adição. Vamos pensar no nosso exemplo:

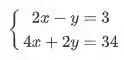
Já vimos que a ideia desse método é somar as duas equações para que elas virem uma só, e fazendo isso, uma das incógnitas vai sumir ou zerar.

Se escolhermos zerar a incógnita , vamos olhar para segunda equação onde temos , e pensar “ que número que se eu somar com ele eu obtenho 0?”

Podemos pensar no , por que assim vamos ficar com

Mas aí, tu olha pra primeira equação e percebe que em vez de você ter um , você tem um . Pronto, esse é o momento exato pra usar nossa gambiarra, vamos novamente pensar, “que número eu multiplico a primeira equação, para ter um -4x?”

Se multiplicarmos a primeira equação por , conseguimos ter o nosso . Então vamos fazer isso:

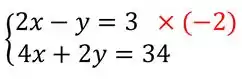
Lembrando que estamos multiplicando a equação TODA, ou seja, todos os membros.

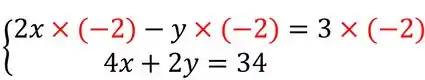
Fazendo isso finalmente chegamos no que queríamos

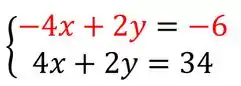
Agora é só somar as duas equações:

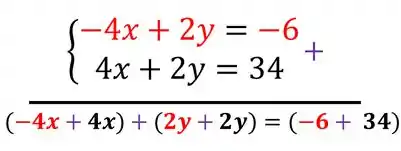
Agora, ficamos só com a equação :

Resolvendo, temos que:

Depois que descobrimos o valor de uma das incógnitas, é só substituir o valor em uma das duas equações, vamos substituir o valor de y na primeira:

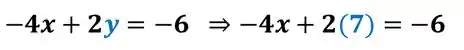
Agora é só resolver essa outra equaçãozinha:

Assim .

Nossa solução é:

Então, é só seguir esses passos que é sucesso:

1º Passo: Escolher qual incógnita você vai zerar
2º Passo: Pensar em um número para multiplicar uma das equações com o intuito de na hora que somar zerar uma das incógnitas.
3º Passo: Multiplicar pelo número escolhido e somar as equações
4º Passo: Resolver a equação e depois substituir o valor encontrado em uma das equações do sistema.

Método da Substituição

Esse método é o seguinte: escolhe uma equação e isola uma incógnita, depois substitui o valor que você encontrou na outra equação. Vamos pegar o nosso sisteminha:

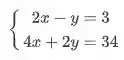
Na primeira equação, vamos isolar uma variável, pode ser o ou o , vamos escolher o :

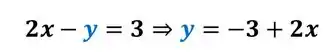
Agora que temos que o valor de , vamos substituir isso na segunda equação:

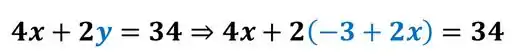
Assim, ficamos com a equação:

Resolvendo, temos que . Depois de descobrir o valor da variável x, voltamos na que isolamos e resolvemos:

Assim, temos que . Nossa solução é:

É isto, então o método da substituição possui os seguintes passos:

1º Passo: Isolar uma incógnita de uma das equações
2º Passo: Substituir a expressão encontrada na outra equação.
3º Passo: Resolver as equações.

Escalonamento- sistema linear com três incógnitas

Belezinha, já aprendemos duas maneiras de como resolver um sistema linear com duas variáveis (ou incógnitas), mas e quando temos ? Existem vários métodos, mas o mais utilizado é o escalonamento. O escalonamento está ligado com escada hehe, você vai pegar seu sistema todo cheio, como esse:

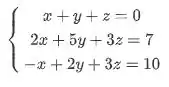
E deixar ele assim:

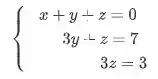
Sim, esses sistemas são equivalentes. Ou seja, possuem o mesmo conjunto solução. Beleza, mas como fazer isso? Existem 4 coisinhas que você pode fazer no seu sistema, e você vai usar elas ao seu favor:

Somar ou subtrair uma equação pela outra;
Multiplicar uma das equações inteira por um número real diferente de zero;
Trocar duas equações de posições entre si;
Multiplicar uma das equações por um número e somá-la ou subtraí-la a outra;

Então, você vai pegar seu sistema, usar suas ferramentas e deixar ela no formato de escada. Assim, vamos fazer o passo a passo de como escalonar esse sistema: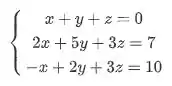

1º Passo: escolher uma das equações e deixar ela como a primeira equação do seu sistema.

DICA: Escolha sempre a que têm os coeficientes que multiplicam as incógnitas, com os valores mais baixos.Nesse caso, vamos escolher a primeira equação mesmo. Então, não vamos trocar nenhuma equação de lugar.

2º Passo: Vamos zerar a primeira incógnita, nesse caso o x, ou seja, nós queremos zerar essa parte:

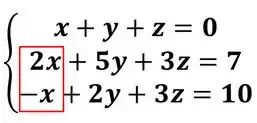
Para isso, vamos usar nossas ferramentas, nós podemos multiplicar uma equação por um número e somar na outra. Sempre vamos multiplicar a equação que escolhemos no passo 1, por um número que vai cancelar o nas outras equações. Então bora lá! Na segunda equação temos:

Nós queremos que o desapareça, então precisamos somá-lo com um , porém na primeira equação, nós temos só . Por isso, vamos multiplicar a primeira linha por e depois vamos somar com a segunda

Multiplicando por :

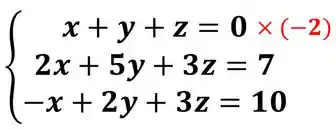
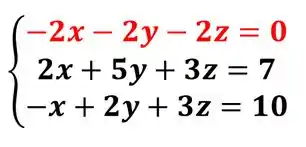
Essa multiplicação vai ser só imaginária, a linha vai continuar como antes. Agora vamos somar essa equação na segunda:

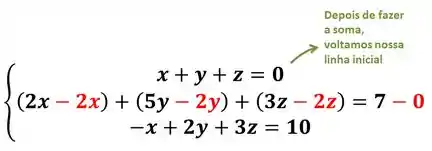
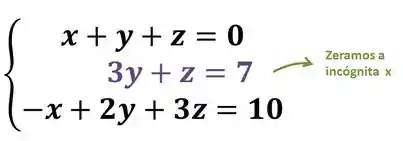
Agora vamos olhar para a terceira equação:

Temos um , para zerar precisamos de um x, e já temos isso na primeira equação, então vamos só somar:

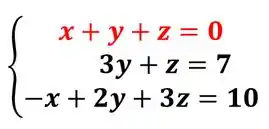
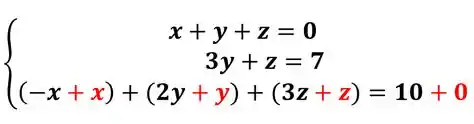
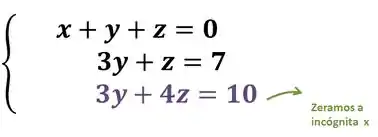
3º Passo: Pronto, a próxima parte da escada que vamos precisar zerar vai ser, ou seja tirar a variável da última equação.

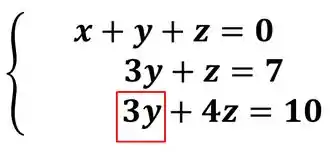
Mas não vamos usar mais a primeira equação, se usarmos ela, o vai voltar e não queremos isso. Então, vamos usar a segunda equação. Na terceira equação temos:

Para zerar o , precisamos somar um , nessa equação. A segunda equação tem , então vamos multiplicá-la por e somar na última :

Multiplicando por

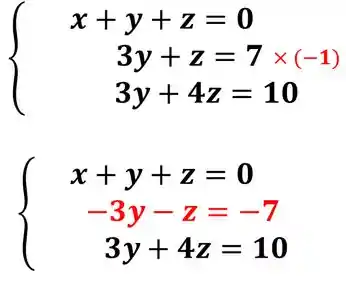
Agora somando:

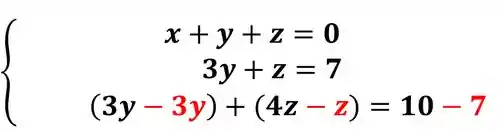
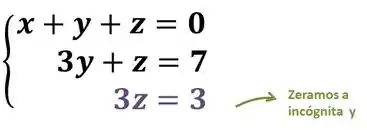
E com isso, você acabou de fazer seu primeiro sistema escalonado, para encontrar os valores é só ir resolvendo as equações e quando encontrar um valor substitui na outra de baixo para cima. Da última equação temos que:

Agora sabendo que , subimos para a segunda equação e colocamos seu valor lá :

E agora vamos para a primeira equação:

Assim, temos que a solução da nossa equação é:

Essa é a ideia do escalonamento, para três incógnita sempre fazemos na mesma sequência, usamos a primeira equação para cancelar a variável das outras duas equações, depois usamos a segunda para zerar o da terceira.

Agora partiu exercícios!

Método da Substituição

Escalonamento- sistema linear com três incógnitas

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

Resolva pelo método da adição:

Passo 1

A ideia do método da adição é você somar as duas equações, e quando fizer isso uma das incógnitas some (ou é zerada).

Vamos olhar para o nosso sistema:

Perceba que se a gente somar as equações, a nossa variável y vai zerar, por que:

Assim, não precisamos fazer modificações, podemos apenas somar nosso sistema.

Passo 2

Somando:

Agora, fazendo essa conta, temos:

Passo 3

Depois de descobrir o valor de uma incógnita, voltamos a uma das primeiras equações e substituímos. Vamos fazer isso na primeira:

Descobrimos que , assim :

Assim, o par ordenado é solução da nossa equação.

Resposta

Exercício Resolvido #2

Elaboração própria

Resolva pelo método da adição:

Passo 1

A ideia do método da adição é você somar as duas equações e zerar ou sumir com uma das incógnitas. Vamos primeiro escolher uma incógnita para zerar, pode ser a . Agora, precisamos pensar em um número para multiplicar a primeira equação, para que na hora que somarmos com a segunda a variável zere. Olhando para a segunda equação:

Temos um , para zerar preccismos soma-lo com um porém na primeira equação temos apenas . Assim, podemos multiplicar nossa primeira equação por , e somar com a segunda.

Passo 2

Fazendo a multiplicação por :

Feito isso, vamos somar as duas equações:

Resolvendo a equação :

Passo 3

Agora que descobrimos o valor de y, vamos voltar em uma das equações iniciais e substituir, vamos pegar a segunda equação:

Substituindo:

Assim, o par ordenado , é solução do nosso sistema.

Resposta

O que é o mesmo que:

Exercício Resolvido #3

Elaboração própria

Resolva pelo método da adição:

Passo 1

Vamos escolher a incógnita x para zerar. Para fazer isso, vamos olhar para a segunda equação:

Temos um , para zerar, precisamos somar com um . Porém se olhamos aa primeira equação:

Nós temos um , para cconsseguirmos o que queremos, basta multiplicarmos primeira equação por

Passo 2

Multiplicando por :

Agora, somando essas duas equações, temos:

Resolvendo a equação:

Passo 3

Agora, é só substituir em uma das equações iniciais, vamos jogar na primeira:

Temos que o par ordenado é solução da nossa equação.

Resposta

Exercício Resolvido #4

Elaboração própria

Resolva pelo método da substituição:

Passo 1

O método da substituição, nada mais é do que isolar uma das incógnitas e substituir na outra equação. Vamos dar uma olhada no nosso sistema:

Já na primeira equação, temos que o x já está isolado:

Agora é só substituir na segunda equação esse valor de x.

Passo 2

Substituindo:

Agora é só resolver essa equaçãozinha :

Passo 3

Agora que descobrimos o valor de y, vamos voltar na primeira equação e substituir

Assim, o par ordenado é solução da nossa equação

Resposta

Exercício Resolvido #5

Elaboração própria

Resolva usando o método da substituição

Passo 1

Para usarmos a substituição, precisamos isolar uma das incógnitas, podemos ver que nesse caso nossa segunda equação já temos o y isolado.

Agora, basta substituirmos o valor dessa incógnita na nossa primeira equação.

Passo 2

Substituindo na primeira equação :

Agora, resolvendo :

Passo 3

Para finalizar, vamos substituir , na segunda equação :

Assim, o par ordenado é solução do nosso sistema.

Resposta

Exercício Resolvido #6

Elaboração própria

Resolva usando o método da substituição

Passo 1

Para usarmos a substituição, precisamos isolar uma das incógnitas, para isso vamos escolher qual incógnita vamos querer isolar, vamos escolher a x.

Na primeira equação temos :

Isolando:

Agora é só ir na segunda equação e substituir essa expressãozinha.

Passo 2

Substituindo na segunda equação :

Agora, resolvendo :

Passo 3

Para finalizar, vamos substituir , na primeira equação :

Assim, o par ordenado é solução do nosso sistema.

Resposta

Exercício Resolvido #7

Elaboração própria

Resolva o sistema:

Passo 1

Podemos ver que esse sistema já está escalonado, assim vamos ir isolando as incógnitas da ultima equação até a primeira.

Terceira equação:

Passo 2

Agora que temos o valor de z, subimos para a segunda equação e substituímos seu valor:

Resolvendo:

Passo 3

Agora subimos para a primeira à equação e substituímos o valor de y e z

Assim temos:

Resposta

Exercício Resolvido #8

Elaboração própria

Resolva o sistema:

Passo 1

Temos um sistema de três incógnitas, para resolver vamos fazer o escalonamento, que é deixar nosso sistema parecido com uma escada, ou seja, vamos zerar essa parte: