Tensão e deformação
Produzido por Erick PinhoTeoria
E aí, tudo bem?
Neste capítulo vamos aprender sobre as propriedades mecânicas dos materiais. É necessário entender como as diferentes propriedades mecânicas são medidas e o que essas propriedades representam. Elas podem ser necessárias para o projeto de estruturas e componentes materiais, para evitar deformações e/ou falhas.

Bora compreender sobres essas propriedades?
Deformação elástica
Eu adoro praticar pilates de solo, e vocês? No pilates de solo é comum usarmos a bola para a realização dos exercícios. Ao sentarmos na bola ela da uma leve comprimida que depois de levantarmos ela retorna ao formato normal.

O quanto o material pode se deformar depende da força aplicada (tensão) imposta. E pode ser definida pela Lei de Hooke:
Onde: σ é a tensão aplicada no corpo (em MPa), E é o módulo de elasticidade do material (em GPa) e ε é deformação sofrida pelo corpo (em mm).
A deformação na qual a tensão e a deformação são proporcionais entre si é denominada de deformação-elástica. Repara que pela equação, o gráfico que representa a Lei de Hooke é uma reta. Poréeem, essa lei não é válida para valores altos de tensão.
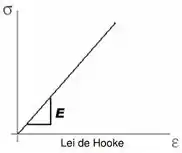
O módulo de elasticidade é uma forma de quantificar a elasticidade do material, ou seja, a “facilidade dele se deformar”.
Pensando dessa forma, qual o material tem um maior módulo de elasticidade? Polimero ou metal? Se vocês pensaram em polímero, pensaram certo :D , pois facilmente conseguimos deformar uma polímero, como por exemplo: puxar uma sacola plástica até arrebenta-la.
Partiu calcular a deformação elástica de uma barra metálica, de 20 mm diâmetro com módulo de elasticidade de 300 GPa se submete a uma força de 25.000 N.
- Primeramente temos que achar a tensão, que tem unidade de pressão. Para acharmos a tensão, é necessário dividir a força pela área .
- Agora que achamos a tensão podemos encontrar a deformação do nosso material, partiu?
Precisamos isolar a variável ε que representa a deformação:
Deformação plástica
Para a maioria dos materiais, a deformação elástica ocorre até valores próximos a 0,005. Ao passar desse valor a tensão aplicada no material não é mais proporcional, ocorrendo então uma deformação permanente não recuperável, ou, deformação plástica.
Como o exemplo da sacola que abordamos antes, após uma determinada força aplicada ela se deforma sem voltar ao seu formato inicial, levando a ruptura do material.
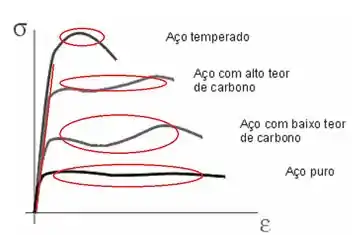
Viram estas marcações em vermelho (linhas e círculos), a linha representa a parte linear do gráfico que corresponde à deformação elástica.
Depois que começa a curva, os círculos representam a deformação plástica, onde mesmo que você retire a tensão aplicada, ela não volta ao seu estado “normal”.
Tensão nominal e deformação nominal
Essas também são conhecidos como tensão e deformação de engenharia.
Quando é feito um ensaio como o de tração, por exemplo, ela é medida de acordo com a força aplicada (carga) e o alongamento da peça.

Nos corpinhos de prova acima, a gente vê uma simulação do ensaio de tração, é como se estivessem tentando esticar a pecinha o máximo possível. Tá vendo que as forças são aplicadas em sentidos opostos?
Para determinarmos a tensão precisamos da área do material! Mas observem, a espessura diminui e o comprimento aumenta, conforme a carga aplicada, dificultando pra nós acharmos a área. A tensão e deformação nominal são então calculadas a partir da área inicial (A0) , considerando que ela se mantenha constante durante o ensaio.
A tensão de engenharia como definida anteriormente, é constituida pela sigla σ , e é definida pela relação:
A deformação de engenharia, como foi determinado anteriormente, é representada pela sigla ε, e é definida pela relação:
sendo: lo o comprimento original e li o comprimento instantâneo antes de ser aplicada carga. ∆l é a variação do comprimento. ε é então adimensional.
Ensaio de tração
Um dos ensaios mecânicos de tensão-deformação mais corriqueiros é o ensaio de tração, que está sendo representado ai na imagem.
Quando é aplicada a carga começa a deformação elástica e depois o surgimento do “pescoço“, que nada mais é do que o alongamento significativo da parte retangular do corpo de prova, diminuindo sua espessura. Com o aumento da tensão, na deformação plástica, o corpo é levado até a ruptura.
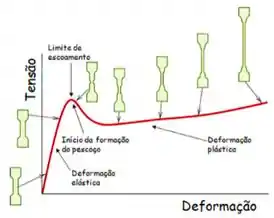
A maquina de ensaios de tração alonga o corpo de prova a uma taxa de velocidade constante, e também mede contínua e simultaneamente a carga e os alongamentos resultantes. O ensaio de leva alguns minutos para ser executado e é destrutivo, ou seja, o corpo de prova não pode ser reaproveitado.
Valores das propriedades mecânicas obtidas a partir do ensaio de tração e diagrama tensão nominal-deformação nominal
Para materiais dúcteis como os matérias metálicos temos o seguinte comportamento:
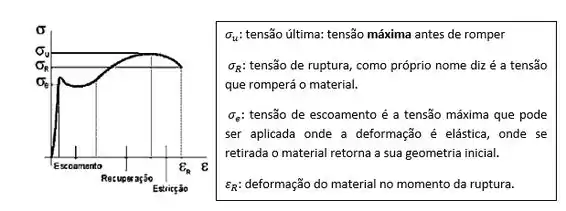
Para materiais frageis como vidro, ferro fundido e etc, temos:

Ductilidade
O alongamento dos corpos de prova ocorre devido a ductilidade do material. Vamos pensar o seguinte, a deformação elástica volta quando a gente tira a carga, certo? Ou seja, a ductilidade é devido apenas à deformação plástica. Vamos ver novamente no gráfico? Toda a parte hachurada corresponde a ductilidade do material.
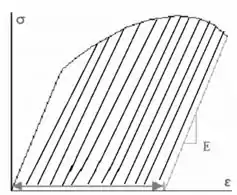
A ductilidade do material que é correspondente a redução da área (RA) do corpo de prova do ensaio pode ser achado através dessa equação:
Onde: Ao: área original (inicial). Af área no momento da fratura.
Deformação plástica
Tensão nominal e deformação nominal
Ensaio de tração
Valores das propriedades mecânicas obtidas a partir do ensaio de tração e diagrama tensão nominal-deformação nominal
Ductilidade
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Quanto ao comportamento dos materiais dúcteis quando submetidos a tração, escolha a alternativa correta:
- Tensão última e a tensão de ruptura são iguais
- A tensão de escoamento é a menor tensão que pode ser aplicada, que se removida o material retrocede a sua geometria inicial.
- Um material dúctil pode ser alongado, flexionado ou torcido, sem romper. Ocorre deformação plástica permanente, após a deformação elástica
Passo 1
Na primeira alternativa a afirmação está incorreta, pois a tensão última e a tensão de ruptura são diferentes.
Passo 2
A tensão de escoamento é a maior tensão que pode ser aplicada.
Passo 3
Um material dúctil pode ser ocorre deformação elástica e plástica
Resposta
Alternativa III
Exercício Resolvido #2
Elaboração própria
Considere as curvas tensão de engenharia versus deformação de engenharia para os três materiais (A, B, C). Marque verdadeiro (V) ou falso (F).
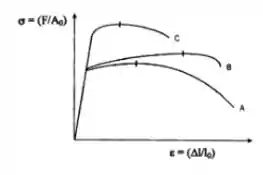
- Os materiais apresentam módulos de elasticidade distintos ( )
- O material C é mais dúctil que os demais ( )
- Ambos materiais são representações de materiais dúcteis ( )
Passo 1
Na primeira alternativa a afirmação está errada, vamos observar o porquê?
O módulo de elasticidade é a parte linear da reta certo? Observem que a reta é igual para todos os materiais, ou seja, apresenta o mesmo módulo de elasticidade.
Passo 2
Na segunda alternativa temos a afirmação que o material C é mais dúctil que os demais, mas vamos relembrar o que é ductilidade? é o grau de deformação que um material suporta até a fratura, ou seja, a área abaixo da curva, representada da deformação até a tensão de ruptura.
Notem que a areai abaixo da curva de C é menor que B que é menor que A, ou seja o material A é mais dúctil.
Passo 3
A terceira alternativa está correta, pois os materiais dúcteis tem como característica a região de deformação elástica + deformação plástica.
Resposta
FFV
Exercício Resolvido #3
Elaboração própria
A inclinação da curva de tensão-deformação na região elástica fornece a seguinte informação:
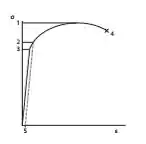
- Tensão de ruptura
- Rigidez
- Deformação plástica
Passo 1
Na primeira alternativa a afirmação está errada, vamos observar o porquê? A tensão de ruptura é indicado pelo número 4. Onde é a tensão que rompe o material.
Passo 2
A região elástica indicada pelo ponto 3 onde nos fornece o módulo de elasticidade do material conforme o ângulo dessa reta linear, o que indica a rigidez do material.
Passo 3
A deformação plástica é toda região que compreende o ponto 2 até o ponto 4.
Resposta
Alternativa B
Exercício Resolvido #4
Elaboração própria
Analisando a curva tensão-deformação, temos que ter mente conceitos para posterior aplicação. Conforme os conceitos aplicados a seguir, determine o que está correto.
- Deformação elástica é a deformação ainda é reversível.
- Tensão máxima: calculada através força sobre área da seção transversal
- A tensão de escoamento antecede a tensão de ruptura para materiais frágeis.
Estão corretos
- I e II, somente.
- I, II e III, somente.
- I, e III, somente.
- Nenhuma das alternativas
Passo 1
Na primeira alternativa a afirmação está correta, após a uma determinada tensão aplicada e quando retirada ela volta ao seu estado normal.
Passo 2
Para encontrarmos a tensão de um material basta aplicar a fórmula a seguir
Passo 3
A tensão de escoamento é igual a tensão de ruptura para os materiais frágeis.
Resposta
Alternativa A
Exercício Resolvido #5
Elaboração própria
Uma barra de aço 1030 de diâmetro 12mm, que apresenta uma rigidez de 120 GPa se submete a uma carga de tensão 25000N. Com essas informações determine a recuperação elástica.
Passo 1
Primeiramente temos que determinar a tensão aplicada a barra, para isso vamos calcular a área?
A área da barra de seção circular é calculada por:
A= πr²
O diâmetro é 12 mm, o raio é a metade certo? 6 mm, mas temos que passar para m, então é só dividirmos por mil, então obteremos 0,006m :D
A= π(0,006) ²
A= 1,13x10-4 m²
Passo 2
Agora que encontramos a área podemos encontrar a tensão, partiu?
Passo 3
Para acharmos a deformação elástica, devemos isolar a variável ε
Resposta
1,842 x 10-3
Exercício Resolvido #6
Elaboração própria
Considere um corpo de prova cilíndrico metálico apresentando de diâmetro e de comprimento que é submetido ao ensaio de tração. Defina seu alongamento quando uma carga de for aplicada e a deformação obtida é de .
Passo 1
Primeiramente devemos determinar a tensão
Observem que a força está em kN ou seja devemos multiplicar 75 por 1000
Passo 2
Agora partiu calcular o alongamento?
Resposta
Exercício Resolvido #7
Elaboração própria
Determine a rigidez de uma liga submetida a um ensaio de tração, cuja a tensão de engenharia é de 115 MPa e deformação 0,0038.
Passo 1
Primeiramente vamos identificar a equação a se utilizar
Passo 2
Lembre-se que MPa (mega pascal) é a mesma coisa que 106Pa
Ou 30,26 GPa (giga pascal)
Resposta
30,26 GPa
Exercício Resolvido #8
Elaboração própria
Em relação a tensão limite de escoamento (σe) escolha a opção incorreta:
- Ponto onde começa a deformação plástica do material.
- O princípio do escoamento tem uma maior deformação em analogia à tensão aplicada
- A passagem do regime elástico para o plástico acontece de modo suave nos materiais metálicos.
Passo 1
Primeira opção correta
Passo 2
Segunda opção correta
Passo 3
A passagem do regime elástico para o plástico acontece de modo abrupto
Resposta
Alternativa III