Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Defeitos Intersticiais

Ver Todos os Exercícios

Teoria

Introdução

E aí galera, tudo tranquilo?

Vamos aprender um pouco sobre defeitos em sólidos cristalinos para mandar super bem nas provas?

Então vamos lá!

Seria possível ter dispositivos eletrônicos do estado sólido sem imperfeições ou defeitos cristalinos?

Sem a presença de defeitos esses dispositivos eletrônicos do estado sólido não existiriam, pois a condutividade eletrônica dos semicondutores depende das impurezas presentes!

Mas não é somente nestes dispositivos que os vários tipos de imperfeições e defeitos alteram propriedades de engenharia importantes, por exemplo, sem os defeitos os cristais não teriam nenhuma cor, os metais seriam muito mais resistentes, os cerâmicos seriam muito mais tenazes e etc...

Assim, os defeitos são bastante importantes, mesmo em concentrações muito pequenas!

Os defeitos nas redes cristalinas são classificados de acordo com a sua geometria e forma, assim os tipos de defeitos podem ser definidos como:

  • Defeitos pontuais: irregularidades que se estendem sobre somente alguns átomos (defeitos adimensionais), podendo ser lacunas (vacâncias), intersticiais ou substitucionais;
  • Defeitos lineares: irregularidades que se estendem através de uma única fileira de átomos (unidimensionais). Nestes estão presentes as famosas discordâncias, que podem ser em hélice ou em cunha;
  • Defeitos planares: irregularidades que se estendem através de um plano de átomos (duas dimensões), podendo ser superfícies exteriores, contornos de grão, interface precipitado;
  • Defeitos volumétricos: defeitos macroscópicos tridimensionais que se estendem sobre o conjunto dos átomos na estrutura ou no volume, por exemplo, as fendas, os poros, as inclusões e os precipitados.

Fique tranquilo!!! Não se espante!!! Veremos cada tipo de defeitos com detalhes.

Defeitos pontuais

Um dos defeitos mais simples que podem existir em uma estrutura cristalina são as lacunas, ou também, conhecidas como vacâncias, que são ausência de átomos em uma posição atômica.

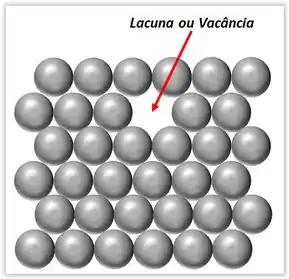
Estas lacunas podem ser originadas durante o processo de solidificação, como resultado de perturbações locais durante o crescimento dos cristais, ou podem ser criadas pelo rearranjo dos átomos de um cristal, devido à mobilidade atômica, ou seja, as lacunas podem mover-se por troca de posição com os átomos vizinhos. Todos os sólidos cristalinos contêm lacunas. A existência das lacunas é explicada pela termodinâmica, ou seja, a presenças delas aumenta a entropia.

Lacunas adicionais podem ser introduzidas nos metais por deformação plástica; através de resfriamento rápido, enclausurando as lacunas; e também através do bombardeamento com partículas de alta energia como, por exemplo, os nêutrons.

A presença destas lacunas significa que as ligações atômicas na vizinhança do defeito não foram satisfeitas. Assim como ocorre nas superfícies. Mas fiquem tranquilos, pois os defeitos superficiais falaremos mais tarde!!!!

Será que é possível calcularmos o número de lacunas em equilíbrio em um sólido?

O número de lacunas para uma dada quantidade de material é função da temperatura de acordo com a equação abaixo:

N V = N ∙ exp ⁡ - Q V k ∙ T

Onde N é o número total de posições atômicas,   N V é o número de lacunas, T é a temperatura absoluta (K), k é a constante de Boltzmann ( 1,38 ∙ 10 - 23 J á t o m o ∙ K ou 8,62 ∙ 10 - 5 e V á t o m o ∙ K ) e Q V é a energia necessária para formação de uma lacuna. Assim, notamos que o número de lacunas aumenta exponencialmente em função da temperatura, ou seja, quanto maior a temperatura maior será o número de lacunas.

Em algumas literaturas podemos identificar o sobescrito L , ao invés do V , ou seja, N V = N L   e Q V = Q L . Usaremos neste material o sobescrito V , que significa vacância.

Vamos entender melhor isso com um exercício?

Exemplo: Calcular a fração de lacunas N V N para o cobre na temperatura ambiente 293 K e na temperatura de 1350 K . Assuma uma energia de ativação de 0,9 e V á t o m o para as duas temperaturas.

  1. Vamos calcular a fração para T = 293 K

    2. N V N = exp ⁡ - 0,9 e V á t o m o 8,62 ∙ 10 - 5 e V á t o m o ∙ K ∙ 293 K

    N V N = e x p ⁡ ( - 35.63 )

    N V N = 3.34 ∙ 10 - 16

  2. Agora vamos calcular a fração para T = 1350 K

N V N = exp ⁡ - 0,9 e V á t o m o 8,62 ∙ 10 - 5 e V á t o m o ∙ K ∙ 1350 K

N V N = e x p ⁡ ( - 7.73 )

N V N = 4.38 ∙ 10 - 4

Observe que nossa afirmação de que quanto maior a temperatura maior será a fração ou o número de lacunas é válida!

Agora que vimos o que são lacunas, vamos entender o que são os defeitos intersticiais!

Defeitos pontuais intersticiais

Antes, porém, de falarmos sobre os defeitos intersticiais é importante nos perguntarmos o que é um interstício?

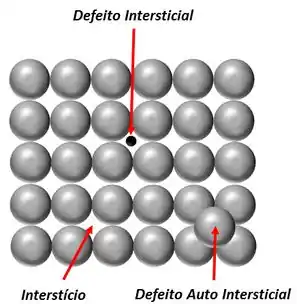
Interstício é um pequeno espaço entre as estruturas cristalinas. Logo, podemos ter dois tipos de defeitos intersticiais: auto intersticial e intersticial.

O auto intersticial é quando o átomo da própria estrutura ocupa o espaço intersticial. Já o defeito intersticial é quando um átomo diferente da matriz ocupa o interstício da estrutura cristalina.

Vamos praticar uma pouco?

Defeitos pontuais

Defeitos pontuais intersticiais

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

O que são defeitos cristalinos e quais os principais tipos de defeitos?

Passo 1

Defeitos cristalinos são imperfeições ou “erros”na estrutura cristalina.

Passo 2

Os principais tipos de defeitos são:

  • Defeitos pontuais: irregularidades que se estendem sobre somente alguns átomos, ou seja, adimensional, podendo ser lacunas, intersticiais ou subtitucionais;
  • Defeitos lineares: alterações que ocorrem na estrutura cristalina que se estendem atráves de uma única fileira de átomos, ou seja, unidimensionais. Aqui estão presentes as discordâncias em cunha e em hélice;
  • Defeitos planares: descontinuações que se estendem atráves de um plano de átomos, ou seja, bidimensionais, que incluem as superfícies externas, limites de grão, contorno de grão, interface precipitado;
  • Defeitos volumétricos: irregularidades macroscopicamente tridimensionais que se estendem sobre o conjunto dos átomos na estrutura ou no volume, podendo ser os precipitados, os poros, as fendas e as inclusões.

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #2

Elaboração própria

Defina o que são lacunas ou vacâncias. Por que os sólidos tendem a ter lacunas e como estas podem ser originadas e introduzidas. E por fim desenhe uma lacuna em uma rede cristalina.

Passo 1

Lacunas são sítios (locais) vagos na rede cristalina.

Passo 2

Os sólidos tendem a possuir lacunas porque ao serem formadas aumentam a entropia (aleatoriedade) de um cristal. Elas podem ser originadas durante a solidificação, como resultado de perturbações locais durante o crescimento dos cristais e rearranjo atômico devido à mobilidade dos átomos, ou seja, as lacunas podem mover-se por troca de posição com os átomos vizinhos. As vacâncias adicionais podem ser introduzidas por resfriamento rápido, deformação plástica, bombardeamento com partículas de alta energia, por exemplo, os nêutrons.

Passo 3

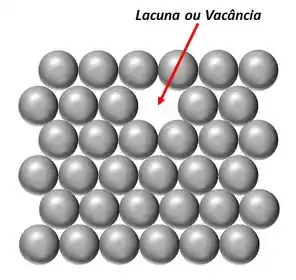
Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #3

Callister W.D. Ciência e Engenharia de Materiais. Sétima edição. Cap.4.

Calcule a fração dos sítios atômicos vagos para o cobre na sua temperatura de fusão de 1084°C. Considere uma energia para formação de lacunas de 0,90 e V á t o m o .

Passo 1

Para o uso correto da equação devemos transformar a temperatura de °C para K.

T K = T ° C + 273

T K = 1084 + 273

T K = 1357 K

Passo 2

Como a energia necessária para a formação de uma lacuna é dada em e V á t o m o , utilizaremos a constante de Boltzmann, como sendo, 8,62 ∙ 10 - 5 e V á t o m o ∙ K .

Passo 3

Agora vamos substituir os valores na equação.

N V N = exp ⁡ - Q V k ∙ T

N V N = exp ⁡ - 0,90 e V á t o m o 8,62 ∙ 10 - 5 e V á t o m o ∙ K   ∙ 1357 K

N V N = 4.56 ∙ 10 - 4

Logo, o fração de vacância ou lacunas para essa temperatura é de 4.56 ∙ 10 - 4 .

Resposta

N V N = 4.56 ∙ 10 - 4

Exercício Resolvido #4

Callister W.D. Ciência e Engenharia de Materiais. Sétima edição. Cap.4.

Calcule o número de lacunas em equilíbrio, por metro cúbico de cobre, a 1000°C. A energia para a formação de uma lacuna é de 0,90 e V á t o m o ; o peso atômico e a massa específica (a 1000°C) para o cobre são de 63,5 g m o l e 8,4 g c m 3 , respectivamente.

Passo 1

Para o uso correto da equação devemos transformar a temperatura de °C para K.

T K = T ° C + 273

T K = 1000 + 273

T K = 1273 K

Passo 2

Como a energia necessária para a formação de uma lacuna é dada em e V á t o m o , utilizaremos a constante de Boltzmann, como sendo, 8,62 ∙ 10 - 5 e V á t o m o ∙ K .

Passo 3

Agora precisamos calcular o N , ou seja, o número total de átomos por unidade de volume para um metal.

N = N A ∙ ρ A C u

onde N A é o número de Avogadro; ρ é a massa específica; e A C u é o peso atômico do cobre.

N = 6,023 ∙ 10 23 ∙ á t o m o s m o l ∙ 8,4 ∙ g 10 - 2 m 3 63,5 g m o l

N = 6,023 ∙ 10 23 ∙ á t o m o s m o l ∙ 8,4 ∙ 10 6 g m 3 63,5 g m o l

N = 8,0 ∙ 10 28 ∙ á t o m o s m 3

Passo 4

Agora vamos substituir os valores na equação.

N V = N ∙ exp ⁡ - Q V k ∙ T

N V = 8,0 ∙ 10 28 ∙ á t o m o s m 3 ∙ exp ⁡ - 0,90 e V á t o m o 8,62 ∙ 10 - 5 e V á t o m o ∙ K   ∙ 1273 K

N V = 2,18 ∙ 10 25 vacância(lacunas)/m³

Logo, o número de lacunas em um metro cúbico de cobre à 1000°C é de 2.18 ∙ 10 25 .

Resposta

N V = 2,18 ∙ 10 25 lacunas/m³

Exercício Resolvido #5

Callister W.D. Ciência e Engenharia de Materiais. Sétima edição. Cap.4.

Calcule o número de lacunas em equilíbrio por metro cúbico de ouro a 900°C. A energia para a formação de uma lacuna é de 0,98 e V á t o m o ; o peso atômico e a massa específica (a 900°C) para o ouro são de 19 6 , 9 g m o l e 1 8 , 63 g c m 3 , respectivamente.

Passo 1

Para o uso correto da equação devemos transformar a temperatura de °C para K.

T K = T ° C + 273

T K = 9 00 + 273

T K = 11 73 K

Passo 2

Como a energia necessária para a formação de uma lacuna é dada em e V á t o m o , utilizaremos a constante de Boltzmann, como sendo, 8,62 ∙ 10 - 5 e V á t o m o ∙ K .

Passo 3

Agora precisamos calcular o N , ou seja, o número total de átomos por unidade de volume para um metal.

N = N A ∙ ρ A A u

onde N A é o número de Avogadro; ρ é a massa específica; e A A u é o peso atômico do ouro.

N = 6,023 ∙ 10 23 ∙ á t o m o s m o l ∙ 18,63 ∙ g 10 - 2 m 3 196,9 g m o l

N = 6,023 ∙ 10 23 ∙ á t o m o s m o l ∙ 18,63 ∙ 10 6 g m 3 196,9 g m o l

N = 5,7 ∙ 10 28 ∙ á t o m o s m 3

Passo 4

Agora vamos substituir os valores na equação.

N V = N ∙ exp ⁡ - Q V k ∙ T

N V = 5,7 ∙ 10 28 ∙ á t o m o s m 3 ∙ exp ⁡ - 0,98 e V á t o m o 8,62 ∙ 10 - 5 e V á t o m o ∙ K   ∙ 1173 K

N V = 3,52 ∙ 10 24 vacância(lacunas)/m³

Logo, o número de lacunas em um metro cúbico de ouro à 900°C é de 3,52 ∙ 10 24 .

Resposta

N V = 3,52 ∙ 10 24 lacunas/m³

Exercício Resolvido #6

Elaboração própria.

Calcule o número de lacunas ( N V ) , por metro cúbico para o ferro, a 875°C. Considere que a energia para a formação de uma lacuna é aproximadamente de 1,07 e V á t o m o . Obs: Consulte a massa específica e a peso atômico em apêndice de livros de ciências do materiais, na internet em tabelas sobre densidades dos materiais e/ou tabelas periódicas.

Passo 1

Para o uso correto da equação devemos transformar a temperatura de °C para K.

T K = T ° C + 273

T K = 875 + 273

T K = 1148 K

Passo 2

Como a energia necessária para a formação de uma lacuna é dada em e V á t o m o , utilizaremos a constante de Boltzmann, como sendo, 8,62 ∙ 10 - 5 e V á t o m o ∙ K .

Passo 3

Consultando uma tabela periódica verifica-se que o peso atômico do ferro é 55,845 g m o l .

Passo 4

Consultando tabela de densidades dos materiais verifica-se que a massa específica ou densidade do ferro é 7,87 g c m 3 .

Passo 5

Agora precisamos calcular o N , ou seja, o número total de átomos por unidade de volume para um metal.

N = N A ∙ ρ A F e

onde N A é o número de Avogadro; ρ é a massa específica; e A F e é o peso atômico do ferro.

N = 6,023 ∙ 10 23 ∙ á t o m o s m o l ∙ 7,87 ∙ g 10 - 2 m 3 55 , 84 5 g m o l

N = 6,023 ∙ 10 23 ∙ á t o m o s m o l ∙ 7,87 ∙ 10 6 g m 3 55 , 84 5 g m o l

N = 8,5 ∙ 10 28 ∙ á t o m o s m 3

Passo 6

Agora vamos substituir os valores na equação.

N V = N ∙ exp ⁡ - Q V k ∙ T

N V = 8,5 ∙ 10 28 ∙ á t o m o s m 3 ∙ exp ⁡ - 1 , 07 e V á t o m o 8,62 ∙ 10 - 5 e V á t o m o ∙ K   ∙ 1148 K

N V = 1,71 ∙ 10 2 4 vacância(lacunas)/m³

Logo, o número de lacunas em um metro cúbico de ferro à 875°C é de 1.71 ∙ 10 24 .

Resposta

N V = 1,71 ∙ 10 24 vacância(lacunas)/m³

Exercício Resolvido #7

Callister W.D. Ciência e Engenharia de Materiais. Sétima edição. Cap.4.

Calcule a energia para a formação de lacunas na prata, sabendo que o número de lacunas em equilíbrio na temperatura de 800°C é de 3,6 ∙ 10 23 m - 3 . O peso atômico e a massa específica (a 800°C) para o prata são de 107 , 9 g m o l e 9 , 5 g c m 3 , respectivamente.

Passo 1

Para o uso correto da equação devemos transformar a temperatura de °C para K.

T K = T ° C + 273

T K = 8 00 + 273

T K = 10 73 K

Passo 2

A fim de termos a energia necessária para a formação de uma lacuna em e V á t o m o , utilizaremos a constante de Boltzmann, como sendo, 8,62 ∙ 10 - 5 e V á t o m o ∙ K .

Passo 3

Agora precisamos calcular o N , ou seja, o número total de átomos por unidade de volume para um metal.

N = N A ∙ ρ A A g

onde N A é o número de Avogadro; ρ é a massa específica; e A A g é o peso atômico do prata.

N = 6,023 ∙ 10 23 ∙ á t o m o s m o l ∙ 9 , 5 ∙ g 10 - 2 m 3 107 , 9 g m o l

N = 6,023 ∙ 10 23 ∙ á t o m o s m o l ∙ 9 , 5 ∙ 10 6 g m 3 1 07 , 9 g m o l

N = 5 , 3 ∙ 10 28 ∙ á t o m o s m 3

Passo 4

Agora vamos isolar o Q V na equação abaixo:

N V = N ∙ exp ⁡ - Q V k ∙ T

N V N = exp ⁡ - Q V k ∙ T

ln ⁡ N V N = ln ⁡ exp ⁡ - Q V k ∙ T

ln ⁡ N V N = - Q V k ∙ T

- ln ⁡ N V N ∙ k ∙ T = Q V ∴ Q V = - ln ⁡ N V N ∙ k ∙ T

Passo 5

Vamos agora substituir os valores dados na equação que manipulamos:

Q V = - ln ⁡ N V N ∙ k ∙ T

Q V = - ln ⁡ 3,6 ∙ 10 23 5,3 ∙ 10 28 ∙ 8,62 ∙ 10 - 5 e V á t o m o ∙ K ∙ 1073 K

Q V = 1,10 e V á t o m o

Resposta

Q V = 1,10 e V á t o m o

Exercício Resolvido #8

Elaboração própria

Calcule a energia para a formação de vacâncias no alumínio, sendo no equilíbrio o número de vacâncias ,a 500°C, é de 7 , 6 ∙ 10 23 m - 3 . A densidade do Al a 500°C é de 2,62 g c m 3 .

Passo 1

Para o uso correto da equação devemos transformar a temperatura de °C para K.

T K = T ° C + 273

T K = 5 00 + 273

T K = 7 73 K

Passo 2

A fim de termos a energia necessária para a formação de uma lacuna em e V á t o m o , utilizaremos a constante de Boltzmann, como sendo, 8,62 ∙ 10 - 5 e V á t o m o ∙ K .

Passo 3

Consultando uma tabela periódica verifica-se que o peso atômico do alumínio é 26 , 982 g m o l .

Passo 4

Agora precisamos calcular o N , ou seja, o número total de átomos por unidade de volume para um metal.

N = N A ∙ ρ A A l

onde N A é o número de Avogadro; ρ é a massa específica; e A A l é o peso atômico do alumínio.

N = 6,023 ∙ 10 23 ∙ á t o m o s m o l ∙ 2,62 ∙ g 10 - 2 m 3 26 , 9 82 g m o l

N = 6,023 ∙ 10 23 ∙ á t o m o s m o l ∙ 2 , 62 ∙ 10 6 g m 3 26 , 9 82 g m o l

N = 5 , 8 ∙ 10 28 ∙ á t o m o s m 3

Passo 5

Agora vamos isolar o Q V na equação abaixo:

N V = N ∙ exp ⁡ - Q V k ∙ T

N V N = exp ⁡ - Q V k ∙ T

ln ⁡ N V N = ln ⁡ exp ⁡ - Q V k ∙ T

ln ⁡ N V N = - Q V k ∙ T

- ln ⁡ N V N ∙ k ∙ T = Q V ∴ Q V = - ln ⁡ N V N ∙ k ∙ T

Passo 6

Vamos agora substituir os valores dados na equação que manipulamos:

Q V = - ln ⁡ N V N ∙ k ∙ T

Q V = - ln ⁡ 7 , 6 ∙ 10 23 5 , 8 ∙ 10 28 ∙ 8,62 ∙ 10 - 5 e V á t o m o ∙ K ∙ 7 73 K

Q V = 0,75 e V á t o m o

Resposta

Q V = 0 , 75 e V á t o m o

Exercício Resolvido #9

Callister - Ciência e Engenharia de Materiais. Uma Introdução - 8°Ed. – Capítulo 4 – Seção Perguntas – Exercício 1

Calcule a fração dos sítios atômicos que estão vagos para o chumbo na sua temperatura de fusão de 327˚C (600 K). Assuma uma energia para a formação de lacunas de 0,55   e V / á t o m o .

Passo 1

Para calcular a fração de sítios vagos adaptaremos a fórmula a seguir:

N v = N exp ⁡ - Q v k T

Onde N v é o número de lacunas, N é o número total de posições atômicas, T é a temperatura em Kelvin, k é a contante de Boltzmann ( 8,62   x   10 - 5 e V / á t o m o . K ) e Q v é a energia necessária para a formação de uma lacuna. Guardou essa fórmula no seu coração? Beleza!

Como o problema quer a fração, o que vamos encontrar na verdade é N v / N !

Sendo assim:

N v N = exp ⁡ - 0,55 8,62   x   10 - 5 x   600 = 2,41   x   10 - 5

Resposta

A fração de sítios vagos para o chumbo à 600 K é 2,41   x   10 - 5 .

Exercício Resolvido #10

Callister - Ciência e Engenharia de Materiais. Uma Introdução - 8°Ed. – Capítulo 4 – Seção Perguntas – Exercício 2

Calcule o número de lacunas por metro cúbico no ferro a 850˚C. A energia para a formação de lacunas é de 1,08   e V / á t o m o . Adicionalmente, a massa específica e o peso atômico para o Fe são de 7,65   g / c m ³ (a 850˚C) e 55,85   g / m o l , respectivamente.

Passo 1

Para calcular o número de lacunas usaremos a fórmula a seguir:

N v = N exp ⁡ - Q v k T

Onde N v é o número de lacunas, N é o número total de posições atômicas, T é a temperatura em Kelvin, k é a contante de Boltzmann ( 8,62   x   10 - 5 e V / á t o m o . K ) e Q v é a energia necessária para a formação de uma lacuna. Bom, mas o problema não deu pra gente N, certo?

Então, a gente pode encontrar N usando a seguinte fórmulinha:

N = N a ρ A

Com essa fórmula a gente chega que N = 5,7   x   10 16 a t o m o s / m ³ ! Bora calcular as lacunas!

Passo 2

Com a fórmula que a gente viu lá em cima a gente vai calcular o número de lacunas:

N v = 5,7   x   10 22 exp ⁡ - 1,08 8,62   x   10 - 5 x   1123

N v = 8,14   x   10 11 l a c u n a s / m ³

Resposta

N v = 8,14   x   10 11 l a c u n a s / m ³

Exercício Resolvido #11

Callister - Ciência e Engenharia de Materiais. Uma Introdução - 8°Ed. – Capítulo 4 – Seção Perguntas – Exercício 3

Calcule a energia de ativação para a formação de lacunas no alumínio, sabendo que o número de lacunas em equilíbrio a 500˚C (773 K) é de 7,57   x   10 23 l a c u n a s / m ³ . O peso atômico e a massa específica (a 500˚C) para o alumínio são, respectivamente, 26,98 g / m o l e 2,62   g / c m ³ .

Passo 1

Para calcular a energia de ativação usaremos a fórmula a seguir:

N v = N exp ⁡ - Q v k T

Onde N v é o número de lacunas, N é o número total de posições atômicas, T é a temperatura em Kelvin, k é a contante de Boltzmann ( 8,62   x   10 - 5 e V / á t o m o . K ) e Q v é a energia necessária para a formação de uma lacuna. Bom, mas o problema não deu pra gente N, certo?

Então, a gente pode encontrar N usando a seguinte fórmulinha:

N = N a ρ A

Com essa fórmula a gente chega que N = 5,85   x   10 28 a t o m o s / m ³ ! Bora calcular o resto!

Passo 2

Com a fórmula que a gente viu lá em cima a gente vai calcular a energia de ativação:

ln ⁡ N v N = - Q v k T 16,376   x   8,62   x   10 - 5   x   773 = Q v

Q v = 0,75 e V / á t o m o

Resposta

Q v = 0,75 e V / á t o m o