Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Defeitos pontuais em sólidos iônicos

Ver Todos os Exercícios

Teoria

E aiiiiiiii galerinha!!! Tudo bem?

Vimos em aulas anteriores que existem defeitos pontuais em compostos metálicos. Mas, será que existem também esses mesmos defeitos para cristais iônicos?

Continue conosco e iremos descobri já já!!!

Nos cristais iônicos, os defeitos pontuais são um pouco mais complexos, devido à necessidade de manter a neutralidade elétrica.

Há duas maneiras principais para se criar defeitos pontuais em sólido iônicos, levando em consideração o fato de manter-se a neutralidade elétrica do sólido:

  • Defeito de Schottky
  • Defeito de Frenkel

O defeito de Schottky há falta de dois íons de cargas contrárias, ou seja, haverá duas lacunas na estrutura: uma do cátion e a outra do ânion. Esse defeito é formado pela remoção de um cátion e de um ânion do interior do cristal e transferindo-os para a superfície externa do cristal. É observado este defeito em compostos altamente iônicos e organizados e com pequena diferença de tamanho entre o cátion e o ânion. Ex.: NaCl, KBr, KCl.

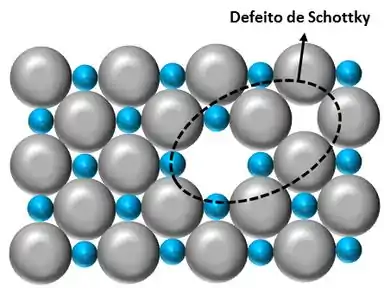
A figura acima mostra duas lacunas: uma com ausência do cátion e a outra com ausência do ânion.

O defeito de Frenkel é formado por uma lacuna catiônica e um cátion intersticial. Esse defeito é formado quando um cátion deixa seu lugar na estrutura, formando uma lacuna, para ocupar um espaço intersticial. Este tipo de defeito ocorre em sólidos iônicos com grandes diferenças de tamanho entre os cátions e ânions. Ex.: AgI, AgBr, AgCl.

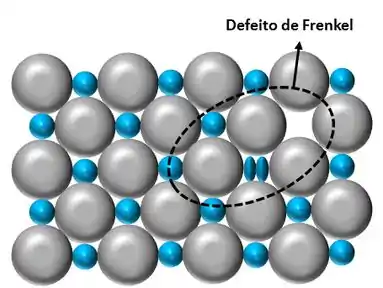
Em relação à densidade do material o defeito de Frenkel não a afeta, pois nesse defeito há somente migração dos íons dentro do cristal, assim preservando tanto o volume quanto a massa. Já para defeito de Schottky a densidade do material é menor que o normal, isso ocorre, pois há migração dos íons para a superfície aumentando o volume do cristal. Como a massa se mantém constante há uma diminuição da densidade.

Especificação da composição

Quando falamos sobre solubilidade de um elemento sólido em outro, podemos fazer alguns questionamentos:

  • Qual é a quantidade de soluto presente no solvente?
  • Qual é a porcentagem em peso desse soluto na solução?
  • Qual é a massa especifica da liga?

Essas e outras perguntas iremos responder no decorrer desse texto. Então, fique ligado para arrebentarmos nas provas!!!!

Há duas maneiras de especificar a composição de uma liga em termos dos seus elementos constituintes:

  1. Porcentagem em peso(%p)
  2. Porcentagem atômica(%a)

Na porcentagem em peso especificamos o peso de um elemento específico em relação ao peso total da liga.

C 1 = m 1 m t o t a l ∙ 100

m t o t a l = m 1 + m 2

C 1 = m 1 m 1 + m 2 ∙ 100

Na equação acima o subindice 1 refere-se a o elemento 1 da solução e o subindice 2 ao elemento 2. Assim, C 1 refere-se a concentração em peso(ou massa) do elemento 1. A mesma lógica é aplicada caso desejássemos obter a concentração em peso(ou massa) do elemento 2, conforme equação abaixo.

C 2 = m 2 m 1 + m 2 ∙ 100

Para a porcentagem atômica (%a) usamos, no lugar da massa, o número de mols de um elemento em relação ao número total de mols de todos os elementos da liga. O número de mols de uma dada massa de um elemento hipotético 1 é:

n m 1 = m 1 ' A 1

Onde n m 1 representa o número de mols, m 1 ' e A 1 representam, respectivamente, a massa (em gramas) e o peso atômico.

Assim a concentração para o elemento 1 em termos da porcentagem atômica em um liga é:

C 1 ' = n m 1 n m 1 + n m 2 ∙ 100

E para o elemento 2:

C 2 ' = n m 2 n m 1 + n m 2 ∙ 100

Às vezes é necessário converter uma porcentagem em peso (ou massa) para uma porcentagem atômica ou vice-versa. Para essas conversões entre composições seguem as equações abaixo:

C 1 ' = C 1 A 2 C 1 A 2 + C 2 A 1 ∙ 100

C 2 ' = C 2 A 1 C 1 A 2 + C 2 A 1 ∙ 100

C 1 = C 1 ' A 1 C 1 ' A 1 + C 2 ' A 2 ∙ 100

C 2 = C 2 ' A 2 C 1 ' A 1 + C 2 ' A 2 ∙ 100

Vamos deduzir umas das equações acima para vermos de onde elas vieram:

Considere a massa total da liga (em gramas) M ' , então:

M ' = m 1 ' + m 2 '

C 1 ' = n m 1 n m 1 + n m 2 ∙ 100

n m 1 = m 1 ' A 1 e n m 2 = m 2 ' A 2

C 1 ' = m 1 ' A 1 m 1 ' A 1 + m 2 ' A 2 ∙ 100

C 1 = m 1 m 1 + m 2 ∙ 100 = m 1 ' M ' ∙ 100

m 1 ' = C 1 ∙ M ' 100

C 1 ' = C 1 ∙ M ' 100 A 1 C 1 ∙ M ' 100 A 1 + C 2 ∙ M ' 100 A 2 ∙ 100

C 1 ' = C 1 100 ∙ A 1 C 1 100 ∙ A 1 + C 2 100 ∙ A 2 ∙ 100

C 1 ' = C 1 A 1 C 1 A 1 + C 2 A 2 ∙ 100

C 1 ' = C 1 A 1 C 1 A 2 + C 2 A 1 A 1 A 2 ∙ 100

C 1 ' = C 1 A 2 C 1 A 2 + C 2 A 1 ∙ 100

Para os cálculos considerando somente dois elementos, temos:

C 1 + C 2 = 100

C 1 ' + C 2 ' = 100

Às vezes queremos as concentrações dos elementos por unidade de volume k g m 3   , logo utilizaremos “duas linhas” nas concentrações expressas em unidade de volume.

C 1 ' ' = C 1 C 1 ρ 1 + C 2 ρ 2 ∙ 10 3

C 2 ' ' = C 2 C 1 ρ 1 + C 2 ρ 2 ∙ 10 3

Para ρ 1 em g c m 3 , C 1 ' ' e C 2 ' ' em k g m 3 .

Abaixo segue as equações para determinação da massa específica e o peso atômico de uma liga binária a partir da composição (%p e %a):

ρ m é d = 100 C 1 ρ 1 ∙ C 2 ρ 2

ρ m é d = C 1 ' A 1 + C 2 ' A 2 C 1 ' A 1 ρ 1 + C 2 ' A 2 ρ 2

A m é d = 100 C 1 A 1 + C 2 A 2

A m é d = C 1 ' A 1 + C 2 ' A 2 100

Vamos praticar uma pouco?

Especificação da composição

Exercícios Resolvidos

Exercício Resolvido #1

Callister W.D. Ciência e Engenharia de Materiais. Sétima edição. Cap.4.

Determine a composição, em porcentagem atômica, de uma liga com 97 %p alumínio e 3 %p cobre.

Passo 1

Vamos escrever a equação que representa o quê precisamos:

C 1 ' = C 1 A 2 C 1 A 2 + C 2 A 1 ∙ 100

Seja C A l ' = C 1 ' , C 1 = C A l , A 1 = A A l ,   C 2 = C C u e A 2 = A C u , onde C A l ' , C A l ,   C C u , A A l e A C u representam, respectivamente, concentração em porcentagem atômica do alumínio, concentração em porcentagem em massa do alumínio, concentração em porcentagem em massa do cobre, massa atômica do alumínio e massa atômica do cobre.

Reescrevendo a equação :

C A l ' = C A l A C u C A l A C u + C C u A A l ∙ 100

Passo 2

Vamos extrair, primeiramente, os dados do problema:

C A l = 97

C C u = 3

Passo 3

Agora retiramos de uma tabela periódica a massa atômica do alumínio e do cobre:

A A l = 26,982 g m o l

A C u = 63,55 g m o l

Passo 4

Agora é só substituir os valores na equação:

C A l ' = 97 ∙ 63 , 55 g m o l 97 ∙ 63 , 55 g m o l + 3 ∙ 26,55 g m o l ∙ 100

C A l ' = 98,72   % a

Passo 5

Para calcular a concentração em peso atômico do cobre baste subtrair 100 da concentração em peso atômico do alumínio. Veja:

C C u ' + C A l ' = 100

C C u ' = 100 - C A l '

C C u ' = 100 - 98,72 = 1,28   % a

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #2

Callister W.D. Ciência e Engenharia de Materiais. Sétima edição. Cap.4.

Qual é a composição , em porcentagem atômica, de uma liga que consiste em 30 %p Zn e 70 %p Cu?

Passo 1

Vamos escrever a equação que representa o quê precisamos:

C 1 ' = C 1 A 2 C 1 A 2 + C 2 A 1 ∙ 100

Seja C Z n ' = C 1 ' , C 1 = C Z n , A 1 = A Z n ,   C 2 = C C u e A 2 = A C u , onde C Z n ' , C Z n ,   C C u , A Z n e A C u representam, respectivamente, concentração em porcentagem atômica do zinco, concentração em porcentagem em massa do zinco, concentração em porcentagem em massa do cobre, massa atômica do zinco e massa atômica do cobre.

Reescrevendo a equação :

C Z n ' = C Z n A C u C Z n A C u + C C u A Z n ∙ 100

Passo 2

Vamos extrair, primeiramente, os dados do problema:

C Z n = 30   % p

C C u = 70   % p

Passo 3

Agora retiramos de uma tabela periódica a massa atômica do zinco e do cobre:

A Z n = 65 , 41 g m o l

A C u = 63,55 g m o l

Passo 4

Agora é só substituir os valores na equação:

C Z n ' = 30 ∙ 63,55 g m o l 30 ∙ 63,55 g m o l + 70 ∙ 65,41 g m o l ∙ 100

C Z n ' = 29,40   % a

Passo 5

Para calcular a concentração em peso atômico do cobre baste subtrair 100 da concentração em peso atômico do zinco. Veja:

C C u ' + C Z n ' = 100

C C u ' = 100 - C Z n '

C C u ' = 100 - 29,40 = 70,60   % a

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #3

Callister W.D. Ciência e Engenharia de Materiais. Sétima edição. Cap.4.

Qual é a composição , em porcentagem em massa, de uma liga que consiste em 6 %a Pb e 94 %a Sn?

Passo 1

Vamos escrever a equação que representa o quê precisamos:

C 1 = C 1 ' A 1 C 1 ' A 1 + C 2 ' A 2 ∙ 100

Seja C P b ' = C 1 ' , C 1 = C P b , A 1 = A P b ,   C 2 ' = C S n ' e A 2 = A S n , onde C P b ' , C P b ,   C S n ' , A P b e A S n representam, respectivamente, concentração em porcentagem atômica do chumbo, concentração em porcentagem em massa do chumbo, concentração em porcentagem atômica do estanho, massa atômica do chumbo e massa atômica do estanho.

Reescrevendo a equação :

C P b = C P b ' A P b C P b ' A P b + C S n ' A S n ∙ 100

Passo 2

Vamos extrair, primeiramente, os dados do problema:

C P b ' = 6   % a

C S n ' = 94   % a

Passo 3

Agora retiramos de uma tabela periódica a massa atômica do chumbo e do estanho:

A P b = 2 07 , 1 9 g m o l

A S n = 118,71 g m o l

Passo 4

Agora é só substituir os valores na equação:

C P b = 6 ∙ 2 07.19 g m o l 6 ∙ 2 07.19 g m o l + 94 ∙ 118.71 g m o l ∙ 100

C P b = 10,02   % p

Passo 5

Para calcular a concentração em porcentagem em massa do estanho basta subtrair 100 da concentração em porcentagem em massa do chumbo. Veja:

C P b + C S n = 100

C S n = 100 - C P b

C S n = 100 - 10 , 02 = 89,98   % p

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #4

Callister W.D. Ciência e Engenharia de Materiais. Sétima edição. Cap.4.

Calcule a composição, em porcentagem em peso, de uma liga que contém 218 kg de titânio, 14,6 kg de alumínio e 9,7 kg de vanádio.

Passo 1

O problema nos pedi os seguintes dados:

C T i =   ? % p

C A l =   ? % p

C V =   ? % p  

Passo 2

Calculamos a composição, em porcentagem em peso, com a seguintes equações:

M = m T i + m A l + m V = 218 k g + 14,6 k g + 9,7 k g = 242,3 k g

C T i = m T i M ∙ 100 = 218 242,3 ∙ 100 = 89,97   % p

C A l = m A l M ∙ 100 = 14,6 242,3 ∙ 100 = 6,03   % p

C V = m A l M ∙ 100 = 9,7 242,3 ∙ 100 = 4,00   % p

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #5

Callister W.D. Ciência e Engenharia de Materiais. Sétima edição. Cap.4.

Qual é a composição, em porcentagem atômica em peso, de uma liga que contém 98g de estanho e 65g de chumbo?

Passo 1

Precisamos calcular o número de mols de estanho e de chumbo. Para isso usaremos a equação abaixo:

n m 1 = m 1 ' A 1

n m S n = m S n ' A S n = 98 g 118,71 g m o l = 0,826 m o l

n m P b = m P b ' A P b = 65 g 207,2 g m o l = 0,314 m o l

Passo 2

Agora para o calculo da composição, em porcentagem atômica em peso, utilizamos a equação:

C 1 ' = n m 1 n m 1 + n m 2 ∙ 100

C S n ' = n m S n n m S n + n m P b ∙ 100 = 0,826 m o l 0,826 m o l + 0,314 m o l ∙ 100 = 72,5   % a

C P b ' = n m P b n m S n + n m P b ∙ 100 = 0,314 m o l 0,826 m o l + 0,314 m o l ∙ 100 = 27 , 5   % a

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #6

Callister W.D. Ciência e Engenharia de Materiais. Sétima edição. Cap.4.

Qual é a composição, em porcentagem atômica em peso, de uma liga que contém 99,7lb de cobre, 102lb de zinco e 2,1lb de chumbo?

Passo 1

Primeiramente devemos converter libra massa para gramas:

m C u ' = 99,7 l b ∙ 453,592 g 1 l b = 45223   g

m Z n ' = 102 l b ∙ 453,592 g 1 l b = 46266   g

m P b ' = 2,1 l b ∙ 453,592 g 1 l b = 953   g

Passo 2

Agora vamos calcular o número de mols:

n m C u = m C u ' A C u = 45223 g 63,55 g / m o l = 712 m o l

n m Z n = m Z n ' A Z n = 46266 g 65,41 g / m o l = 7 07 m o l

n m P b = m P b ' A P b = 953 g 207 , 2 g / m o l = 4,6 m o l

Passo 3

Agora finalizamos com o calculo da concentração, em porcentagem atômica em peso, de cada elemento:

C C u ' = n m C u n m C u + n m Z n + n m P b ∙ 100 = 712 m o l 712 m o l + 707 m o l + 4,6 m o l ∙ 100 = 50   % a

C Z n ' = n m Z n n m C u + n m Z n + n m P b ∙ 100 = 707 m o l 712 m o l + 707 m o l + 4,6 m o l ∙ 100 = 49,7   % a

C P b ' = n m Z n n m C u + n m Z n + n m P b ∙ 100 = 4,6 m o l 712 m o l + 707 m o l + 4,6 m o l ∙ 100 = 0 , 3   % a

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #7

Callister W.D. Ciência e Engenharia de Materiais. Sétima edição. Cap.4.

A concentração de carbono em uma liga ferro-carbono é de 0,15 %p. Qual é a concentração em quilogramas de carbono por metro cúbico da liga? Seja ρ C = 2,25 g / c m 3 e ρ F e = 7,87 g / c m 3 .

Passo 1

Quando desejamos obter a concentração dos elementos por unidade de volume k g m 3   , utilizamos a seguinte equação:

C 1 ' ' = C 1 C 1 ρ 1 + C 2 ρ 2 ∙ 10 3

Seja, C 1 ' ' = C C ' ' , C 1 = C C , ρ 1 = ρ C , C 2 = C F e e ρ 2 = ρ F e , então:

C C ' ' = C C C C ρ C + C F e ρ F e ∙ 10 3

Passo 2

Os dados do problema são:

C C = 0,15   % p

Como o solução é de dois elementos temos:

C C + C F e = 100

Assim:

0,15   % p + C F e = 100

C F e = 100 - 0,15 % p = 99,85   % p

Passo 3

Agora é só colocarmos os dados na equação.

C C ' ' = 0,15 0,15 2,25 ∙ g c m 3 + 99,85 7,87 ∙ g c m 3 ∙ 10 3 = 11,8 k g m 3

Resposta

C C ' ' = 11,8 k g m 3

Exercício Resolvido #8

Askeland D.R e Wright W.J. Ciência e Engenharia dos Materiais. Terceira edição.

Suponha a presença de um defeito de Schottky a cada dez células unitárias do MgO. O MgO exibe a mesma estrutura cristalina do cloreto de sódio e parâmetro de rede de 0,396 n m . Calcule:

  1. O número de lacunas de ânions por c m 3 ; e
  2. A massa especifica da cerâmica.

Passo 1

  1. O volume da célula unitária do MgO é:

    2. V M g O = a 3 = 0,396 ∙ 10 - 7 c m 3 = 6,21 ∙ 10 - 23 c m 3

    Como em cada célula temos 1 10 de vacâncias, logo:

    1 10 V a c â n c i a V M g O = 1 10 V a c â n c i a 6,21 ∙ 10 - 23 c m 3 = 1,61 ∙ 10 21 V a c â n c i a / c m 3

    Passo 2

  2. A estrutura cristalina do MgO é CFC, mesma do NaCl, assim, o número de átomos por célula unitária é 4.

ρ = n ∙ A V c ∙ N A

Onde n é o número de átomos por célula unitária, A o peso atômico, V c   o volume da célula unitária, N A o número de Avogadro e ρ a massa especifica. Em cada dez células unitárias temos uma vacância. Logo, em dez células unitárias teremos 39 cations de M g + 2 e 39 ânions de O - 2 , ou seja, 39 / 40 ions de M g O

ρ M g O = n ∙ ( A M g + A O ) V M g O ∙ N A

ρ M g O = 4 á t o m o s c e l u l a   u n i t á r i a ∙ 24,305 g m o l + 16 g m o l ∙ 39 / 40 6,21 ∙ 10 - 23 c m 3 c e l u l a   u n i t á i r a ∙ 6,022 ∙ 10 23 á t o m o s m o l = 4,20 ∙ g c m 3  

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #9

Callister - Ciência e Engenharia de Materiais. Uma Introdução - 8°Ed. – Capítulo 4 – Seção Perguntas – Exercício 14

Calcule o número de átomos por metro cúbico no alumínio.

Passo 1

Pra encontrar o número de átomos por metro cúbico do alumínio, vamos precisar saber sua massa específica e sua massa molar. Consultando nossa querida internet temos que: ρ A l = 2,71   g / c m ³ e A A l = 26,98   g / m o l . Então a primeira coisa que vamos fazer é descobrir quantos moles existem por metro cúbico!

2,71   ÷ 26,98 = 0,1   m o l / c m ³

Passo 2

Agora a gente só precisa relacionar esse número de moles com número de átomos. Pra isso vamos usar o número de Avogadro!

1   m o l - 6,023   x   10 23

0,1   m o l - x

x = 6,023   ×   10 22   á t o m o s

Agora só pra ficar nas unidades certinhas, como queremos em metros cúbicos, vamos fazer essa conversão:

1   m 3 = 10 6   c m ³

Logo,

x = 6,023   ×   10 22 × 10 6   á t o m o s / m ³ = 6,023 × 10 28   á t m o s / m 3

Resposta

6,023   ×   10 28   á t o m o s / m ³

Exercício Resolvido #10

Callister - Ciência e Engenharia de Materiais. Uma Introdução - 8°Ed. – Capítulo 4 – Seção Perguntas – Exercício 15

A concentração de carbono em uma liga ferro-carbono é de 0,15%p. Qual é a concentração em quilogramas de carbono por metro cúbico da liga?

Passo 1

Pra encontrar a concentração em termos de massa por volume vamos usar a seguinte fórmula:

C 1 ' ' = C 1 C 1 ρ 1 + C 2 ρ 2 x   10 ³

Onde C 1 e C 2 são as concentrações em porcentagens atômicas e C 1 ' ' é a porcentagem em k g / m ³ . Ah, e só pra complementar, se a gente não tivesse multiplicando por 10³ a gente teria o resultado em g / c m ³ .

Beleza, então agora a gente precisa saber a porcentagem de ferro na liga e as massas específicas do carbono e do ferro! O primeiro é fácil, só subtrairmos a porcentagem de carbono de 100%:

% p F e = 100 - 0,15 = 99,85 %

Agora as massas específicas vamos ter que consultar a nossa querida internet ou a tabela mais próxima de você!

ρ C = 2,25 g / c m ³

ρ F e = 7,87   g / c m ³

Passo 2

Agora a gente só precisa substituir na fórmula os dados que a gente tem!

C C ' ' = 0,15 0,15 2,25 + 99,85 7,87 x   10 ³

C c ' ' = 11,76   k g / m ³

Resposta

C c ' ' = 11,76   k g / m ³

Exercício Resolvido #11

Callister - Ciência e Engenharia de Materiais. Uma Introdução - 8°Ed. – Capítulo 4 – Seção Perguntas – Exercício 16

Determine a massa específica aproximada de um latão com alto teor de chumbo que possui a composição 64,5%p Cu, 33,5%p Zn e 2%p Pb.

Passo 1

Pra encontrar a massa específica vamos usar a seguinte fórmula:

ρ m é d = ( C 1 ρ 1 + C 2 ρ 2 + C 3 ρ 3 ) 100

Onde C 1 , C 2 e C 3 são as concentrações em porcentagens atômicas e ρ corresponde à massa específica.

Beleza, então agora a gente precisa saber as massas específicas do materiais da liga! Pra isso, vamos ter que consultar a nossa querida internet ou a tabela mais próxima de você!

ρ C u = 8,94 g / c m ³

ρ Z n = 7,12 g / c m ³

ρ P b = 11,35 g / c m ³

Passo 2

Agora a gente só precisa substituir na fórmula os dados que a gente tem!

ρ m é d = ( 64,5   x   8,94 + 33,5   x   7,12 + 2   x   11,35 ) 100

ρ m é d = 8,38   g / c m ³

Resposta

ρ m é d = 8,38   g / c m ³

Exercício Resolvido #12

Livro Callister, Problema 4.18

Uma liga hipotética é composta de 12,5 % p do metal A e 87,5 % p do metal B. Se as massas específicas dos metais A e B são 4,27 e 6,35   g   / c m 3 , respectivamente, enquanto seus respectivos pesos atômicos são 61,4   e 125,7 g / m o l   , determine se a estrutura cristalina para essa liga é cúbica simples, cúbica de faces centradas ou cúbica de corpo centrado. Assuma um comprimento da aresta da célula unitária de 0,395 n m .

Passo 1

Para resolver esse problema, é necessário empregar a Equação 3.5; nessa expressão, a densidade e o peso atômico serão calculados para a liga - isto é,

ρ a v e = n A a v e V C N A

Na medida em que para cada uma das estruturas cristalinas possíveis, a célula unitária é cúbica, então V C = a 3 , ou,

ρ a v e = n A a v e a 3 N A

E, para determinar a estrutura cristalina, é necessário resolver para n, o número de átomos por unidade de célula. Para n = 1, a estrutura cristalina é simples cúbica, enquanto que para n valores de 2 e 4, a estrutura cristalina será CCC ou CFC, respectivamente. Quando resolvemos a expressão acima para n, o resultado é o seguinte,

n = ρ a v e a 3 N A A a v e

As expressões para A a v e e ρ a v e são encontradas nas Equações 4.11a e 4.10a, respectivamente, as quais, quando incorporadas na expressão acima, produzem

n = 100 C A ρ A + C B ρ B a 3 N A 100 C A ρ A + C B ρ B

Passo 2

Substituição dos valores de concentração (ou seja, C A =   12,5 % em peso e C B =   87,5 % em peso), bem como valores para os outros parâmetros dados na declaração do problema, dados na equação acima

n = 100 12.5 w t % 4.27 g / c m 3 + 87.5 w t % 6.35 g / c m 3 ( 3.95 × 1 0 - 8 n m ) 3 ( 6.022 × 1 0 23 a t o m s / m o l ) 100 12.5 w t % 4.27 g / c m 3 + 87.5 w t % 6.35 g / c m 3 = 2.0   á t o m o s / c é l u l a   u n t á r i a

Portanto, com base nesse valor, a estrutura do cristal é cúbica no corpo.

Resposta

A estrutura do cristal é cúbica no corpo.