Discordância em Aresta
Teoria
Faaaaaaala aí galera!!! Tudo certinho?
Será que as imperfeições são importantes por tornar o material metálico muito mais dúctil devido à sua presença?
Para respondermos essa pergunta precisamos entender um pouco sobre as tais discordâncias em linhas.
Afinal o quê é uma discordância em aresta?
São defeitos lineares que originam uma distorção da rede cristalina centrada em torno de uma linha!
Caaaalma. Fique tranquilo, vamos te explicar!
Vamos imaginar uma estrutura cristalina perfeita como da figura abaixo:
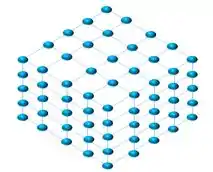
Agora vamos olhar para essa estrutura de frente, como a figura abaixo.
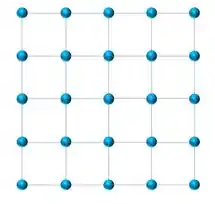
Agora retiramos da estrutura acima um semiplano de átomo, conforme figura abaixo.
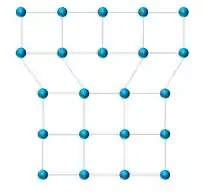
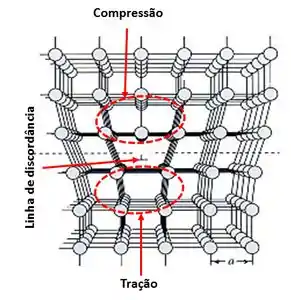
O que formamos é uma estrutura tridimensional com uma linha separando a seção perfeita da seção deformada do material. E isso é o que chamamos de discordância em aresta ou cunha. O esquema abaixo mostra uma discordância em aresta em uma estrutura cristalina. Caso percorrêssemos no sentido horário em torno da discordância, a partir do ponto x, e percorrendo o mesmo número de distâncias atômicas em cada direção, terminaremos no ponto y, uma distância atômica afastada do ponto de partida. O vetor necessário para completar essa volta, chamamos o de vetor de Burgers b. Neste caso o vetor de Burgers é perpendicular à linha de discordância. A linha de discordância no exemplo abaixo entra na sua tela.
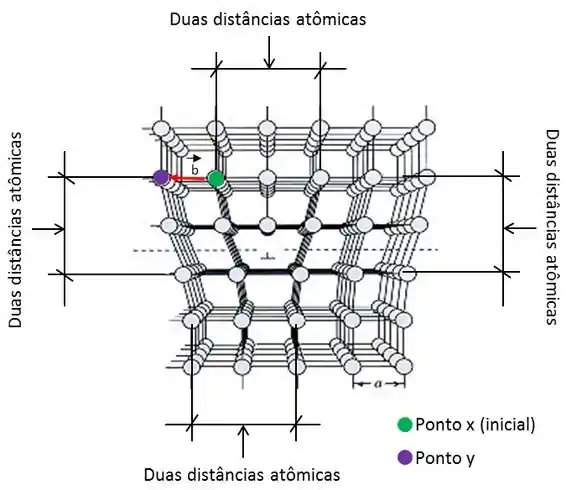
As discordâncias são originadas durante a solidificação dos sólidos cristalinos, por deformação plástica, por condensação de lacunas e por desajustamentos atômicos em soluções sólidas. Elas são defeitos de não equilíbrio e armazenam energia na região distorcida da rede cristalina, em torno da discordância.
Frequentemente, se utiliza o símbolo abaixo para designar um defeito de discordância em aresta. O eixo longo do símbolo aponta em direção ao semiplano adicional.
Nesse tipo de discordância existem duas regiões: uma região em compressão, do lado em que há o semiplano adicional, e uma região em tração, abaixo do semiplano adicional. Conforme ilustrado na figura acima.
Ao aplicamos uma do sólido. Esse movimento é chamado de movimento de discordância.
A quantidade de discordâncias pode ser controlada por tratamentos térmicos e/ou pelo grau de deformação plástica imposta.
Metais que sofrem deformação a frio há um aumento na quantidade de discordância.
O aumento da temperatura facilita os movimentos de discordâncias, o que pode favorecer a diminuição destas.
Portanto, a deformação plástica de um metal depende da habilidade das discordâncias moverem-se.
Quando impedimos ou restringimos o movimento das discordâncias proporcionamos maior dureza e mais resistência ao material.
Vamos praticar?
Exercícios Resolvidos
Exercício Resolvido #1
Askeland D.R e Wright W.J. Ciência e Engenharia dos Materiais. Terceira edição.
Desenhe um circuito de Burgers em torno da discordância mostrada na figura abaixo. Indique claramente o vetor de Burgers que você encontrou. Que tipo de discordância é essa? Em qual direção a discordância irá se mover devido à tensão de cisalhamento aplicada? Consulte os eixos das coordenadas apresentados para dar suas respostas.
Passo 1
Primeiramente vamos caminhar em torno da discordância sempre com a mesma distância atômica. Ao final traçarmos o vetor de Burgers partindo do ponto inicial ao ponto final. Pronto, aí estará nosso vetor de Burgers!!!
Passo 2
Essa é uma discordância em aresta pois o vetor de Burgers é perpendicular à linha de discordância.
Passo 3
Para uma discordância em aresta o plano de escorregamento é obtido a partir do vetor de Burgers e da linha de discordância. E para que ela mova-se um tensão cisalhante deve agir paralelamente ao vetor de Burgers, assim a discordância irá se mover no sentido do eixo , ou seja, no sentido de “empurar” o semiplano para a direita.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Askeland D.R e Wright W.J. Ciência e Engenharia dos Materiais. Terceira edição.
O cristal da figura abaixo contém duas discordâncias A e B. Se for aplicada uma tensão de cisalhamento ao cristal, como é mostrado, o que acontecerá às discordâncias A e B.
Passo 1
Primeiramente vamos caminhar em torno das discordâncias sempre com a mesma distância atômica. Ao final traçarmos o vetor de Burgers partindo do ponto inicial ao ponto final. Pronto, aí estarão nossos vetores de Burgers!!!
Passo 2
Essa é uma discordância em aresta pois o vetor de Burgers é perpendicular à linha de discordância. Nota-se, também, que os vetores de Burgers estão em sentido oposto, assim os semiplanos caminharão em sentidos opostos até que encontrem-se e aniquilam-se.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição. Cap.4.
Para se ter uma perspectiva das dimensões dos defeitos atômicos, considere uma amostra metálica com uma densidade de discordâncias de .Suponha que todas as discordâncias em um volume de tenham sido de alguma maneira removidas e unidas por suas extremidades. Qual será o comprimento (em ) que essa cadeia terá? Agora, suponha que a densidade seja aumentada para por trabalho a frio. Qual seria o comprimento da cadeia de discordâncias em do material?
Passo 1
Vamos escrever em forma de equação a densidade de discordâncias:
Onde, é o comprimento das discordâncias, é o volume do material e é a densidade de discordâncias dada em ou .
Passo 2
Sabemos que:
e
Passo 3
Agora vamos substituir os valores fornecidos na equação:
Passo 4
Agora faremos o mesmo procedimento do item anterior para calculamo o comprimento das discordâncias com a densidade de :
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Askeland D.R e Wright W.J. Ciência e Engenharia dos Materiais. Terceira edição.
Que massa de alumínio, com densidade de discordância de , é necessária para gerar um comprimento total de discordâncias que se estenda entre as cidades de Nova York e Los Angeles (cerca de 4860 quilômetros)?
Passo 1
Vamos escrever em forma de equação a densidade de discordâncias:
Onde, é o comprimento das discordâncias, é o volume do material e é a densidade de discordâncias dada em ou .
Passo 2
Sabemos que:
e
Passo 3
Agora vamos substituir os valores fornecidos na equação:
Passo 4
A densidade do alumínio é dado pela equação:
Onde é o número de átomos associados a cada célula unitária, é o peso atômico, é o volume da célula unitária e é o número de Avogadro
A estrutura cristalina do alumínio é CFC, portanto , onde .
O
Para a estrutura CFC , assim:
Passo 5
Agora vamos calcular a massa de alumínio com a equação abaixo:
Resposta
Exercício Resolvido #5
Concurso: Ministério da Defesa - Comando da Aeronáutica 2017.
Em sólidos cristalinos, a deformação plástica envolve, na maioria das vezes, o movimento de discordância. Analise as afirmativas a seguir sobre as características das discordâncias e o seu envolvimento em um processo de deformação plástica.
I. Em uma discordância de aresta, existe uma distorção localizada da rede cristalina ao longo da extremidade de um semi plano adicional de átomos, que também define a linha da discordância.
II. Uma discordância espiral pode ser considerada como sendo o resultado de uma distorção por cisalhamento.
III. Durante a deformação plástica, o número de discordância aumenta drasticamente.
IV. A densidade de discordância em um material é expressa como a área total de discordância por unidade de volume.
V. As discordâncias se movem com o mesmo grau de facilidade sobre todos os planos cristalográficos de átomos e em todas as direções cristalográficas.
Está correto apenas o que se afirma em:
a) I e II.
b) IV e V.
c) I, II e III.
d) III, IV e V.
Passo 1
O item IV e V estão incorretos.
No item IV o erro está na “área total discordância”. O correto é : A densidade de discordância em um material é expressa como o comprimento total de discordâncias por unidade de volume.
Passo 2
No item V o erro está em: “se movem com o mesmo grau”. O correto é: As discordâncias não se movem com o mesmo grau de facilidade sobre todos os planos cristalográficos de átomos e em todas as direções cristalográficas.
Resposta
Letra: c
Exercício Resolvido #6
FUNDEP / UFMG Universidade Federal dos Vales do Jequitinhonha e Mucuri - MG.
A deformação plástica em metais ocorre por meio da movimentação de discordâncias sobre planos e direções cristalográficas específicas.
Em relação a esses defeitos, é correto afirmar que são defeitos:
- pontuais da estrutura atômica.
- planares da estrutura atômica.
- lineares da estrutura atômica.
- volumétricos da estrutura atômica.
Passo 1
A deformação plástica em metais ocorre por meio da movimentação de discordâncias. Estas são defeitos lineares da estrutura atômica, pois forma em torno de uma linha regiões de compressão e tração na rede cristalina.
Resposta
Letra: C
Exercício Resolvido #7
CESPE/CEBRASPE Polícia Científica de Pernambuco - PE.
Acerca do comportamento de materiais quando submetidos a processos de conformação, assinale a opção correta.
- O encruamento no material ocorre quando as discordâncias se deslocam para regiões mais energéticas do material como os contornos de grãos, gerando como consequência o aumento na dureza.
- O aumento do tamanho de grão provocado por um processo de laminação a quente aumenta a resistência do material.
- Materiais policristalinos com grãos menores são, em geral, mais dúcteis que os mesmos materiais com granulação mais grosseira.
- A deformação plástica do material tem pouca influência nos tamanhos de grãos e, consequentemente, na resistência mecânica do material.
- O endurecimento de um metal por encruamento provocado pela laminação a quente é fator importante na propriedade final do material.
Passo 1
No processo de laminação a quente há um refino de grãos gosseiros para grãos mais refinados. Além disso, nesse processo há diminuição da resistência do material ocorre pois o metal é aquecido até a temperatura de recristalização, portanto nessa temperatura os grãos da microestrutura começam a se transformar em novos grãos equiaxiais e com baixa densidade de discordâncias, diminuindo, assim, sua resistência mecânica. Por esse motivo a alternativa B) está incorreta.
Passo 2
Os contornos de grão são defeitos de superfícies que impedem a movimentação das discordâncias, portanto, comparando estruturas iguais porém com tamanho de grão diferente, quanto maior o tamanho de grão mais facilmente move-se as discordâncias. Por esse motivo as letras C) e D) estão incorretas.
Passo 3
A alternativa E) está incorreta pois trabalho à quente não promove o encruamento.
Resposta
Letra: A
Exercício Resolvido #8
Elaboração própria.
Em relação aos defeitos cristalinos, assinale a alternativa falsa.
- Todo defeito cristalino causa uma distoção no reticulado do cristal.
- As lacunas são um defeito que oportuniza a difusão de átomos substitucionais em sólidos.
- Em uma solução sólida, o soluto pode ser intersticial quando seu diâmetro atómico é similar ao do solvente.
- A interação entre defeitos cristalinos ocorre devido às tensões geradas em tomo dos defeitos.
- O contomo de grão é a região de transição entre cristais que têm diferente orientação cristalina
Passo 1
Em uma solução sólida, o soluto deve possuir um diâmetro substancialmente menor do que o do solvente, a fim de preencher os espaços intersticiais.
Resposta
Letra: C