Regra da Alavanca
Produzido por Erick PinhoTeoria
Chegou a hora de aprender a Regra da Alavanca de um jeito rápido e descomplicado com o RespondeAí! Siga o mestre 😆
Uma coisa bem importante que aprendemos em Ciência dos Materiais é o Diagrama de Fases.
A regra da alavanca serve para nos ajudar a determinar a fração molar
-Hãam?!
Vou te dar um exemplo! Imagina uma mistura de cobre
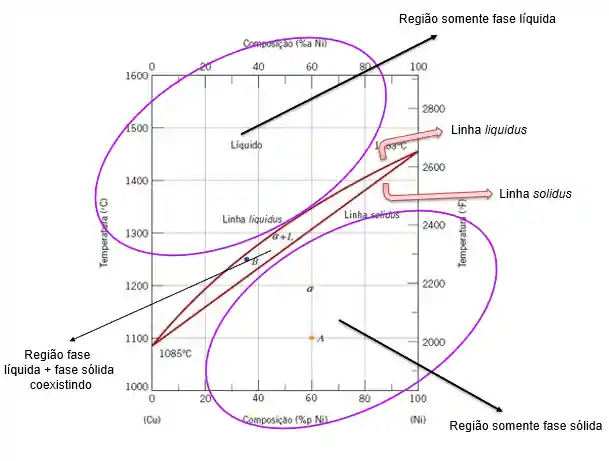
Agora, imagina que nós temos uma composição
SIIIMMM!! É aí que entra a Regra da Alavanca.
-E como funciona isso?!
Se liga nesse vídeozinho iradoso que o RespondeAí preparou sobre regra da alavanca!
Ou se você preferir, segue comigo para um resumo em texto 👇
Para aplicar a regra da alavanca a primeira coisa que temos que fazer é traçar uma linha que chamamos de linha de amarração. Ela é uma linha horizontal (isotérmica - temperatura constante) e liga o ponto que queremos saber a composição do líquido e sólido, nesse caso exemplo é o ponto
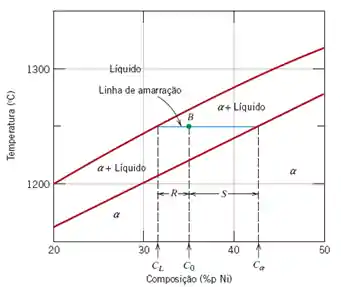
Como podemos ver na figura, a partir da linha de amarração a gente consegue traçar três linhas verticais:
- A primeira iniciando na interseção da linha de amarração com a linha liquidus e se extendendo até o eixo
- nos fornece a composição de niquel na fase líquida ; - A segunda iniciando na interseção da linha de amarração com o ponto
e se extendendo até o eixo - nos fornece a composição de níquel global da liga ; - E por último, a terceira iniciando na interseção da linha de amarração com a linha solidus e se extendendo até o eixo
- nos fornece a composição de niquel na fase sólida ;
Pelo próprio diagrama de fases a gente consegue ler o valor de
Além dessas três linhas podemos também definir duas distâncias horizontais:
- Distância
que liga a primeira linha vertical à segunda e representa a porcentagem da fase sólida, e; - Distância
que liga a segunda linha vertical à terceira e representa a porcentagem da fase líquida
Que são dadas por:
E agora, aplicamos de fato a regra da alavanca, que diz que as frações mássicas das fase líquida e sólidas, representadas por
Substituindo os valores para esse nosso caso específico, temos:
Beleza, encontramos várias coisas com a Regra da Alavanca. Mas o que tudo isso quer dizer?
Para o ponto

É isso aí pessoal, agora vamos praticar bastante 🎉
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
De forma simplificada determine o que são os diagramas de fases de um composto e cite um exemplo de aplicação.
Passo 1
Nada melhor pra entender o que é um diagrama de fase do que olhando pra um!
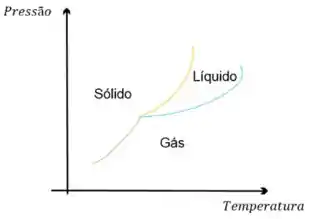
Esse diagrama de fases unitário, de apenas uma substância, mostra pra gente a fase que ela se encontra dados temperatura e pressão.
Passo 2
Agora vamos olhar aqui um diagrama de fases binário, de duas substâncias:
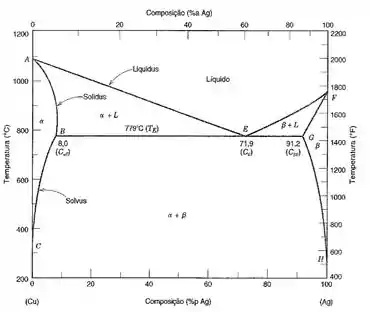
Esse diagrama mostra pra gente as fases presentes dados temperatura e composição!
Passo 3
O que podemos concluir disso então?
Que um diagrama de fases mostra pra gente as fases presentes de um material dadas 2 condições!
Resposta
Diagrama de fases é uma representação gráfica que indica as fases presentes dadas duas condições físico-químicas do material.
Exercício Resolvido #2
Universidade Paulista- UNIP
Uma liga contendo aproximadamente 90% de prata e 10% de cobre é aquecida a 600°C e a 800°C.
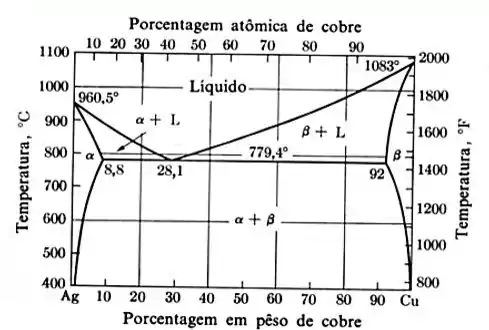
Passo 1
Vamos delimitar o traçado para as 2 temperaturas (linhas horizontais) e o teor de cobre (10%) com uma linha vertical.
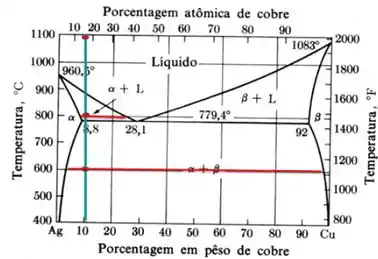
Passo 2
Agora iremos calcular para a temperatura de 600°C, nota-se que é uma mistura de α+β
Lembrando a fórmula:
Se temos 93,6% de alfa na composição, então teremos consequentemente (para fechar 100%) 6,4% β.
Passo 3
Agora iremos calcular para a temperatura de 800°C, nota-se que é uma mistura de α+L
Se temos 88,3% de alfa na composição, então teremos consequentemente (para fechar 100%) 11,7% L.
Resposta
Para 600°C: 93,6% de alfa e 6,4% β.
Para 800°C: 88,3% de alfa e 11,7% L.
Exercício Resolvido #3
Universidade Paulista- UNIP
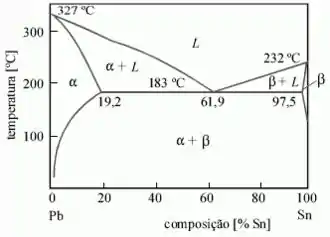
Para uma liga de solda com 40% de estanho e 60% de chumbo a 150°C. Determine as fases presentes?
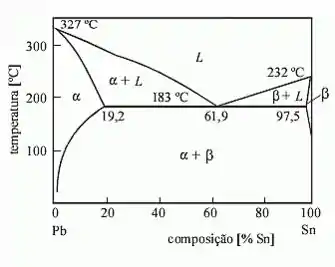
Passo 1
Vamos delimitar o traçado para as 2 temperaturas (linhas horizontais) e o teor de estanho (40%) com uma linha vertical.
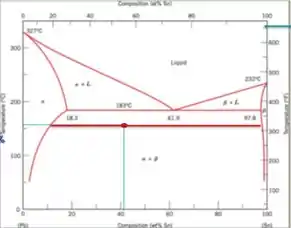
Passo 2
Nota-se que é uma mistura de α+β
C α: observando a região alfa e a linha verde pequena rebatemos ela no eixo da composição e nos da 10% de Sn.
Co: O próprio enunciado nos oferece a proporção de 40% de Sn
C β: observando a região beta rebatemos ela no eixo da composição e nos da 98% de Sn
Resposta
C α= 10% de Sn
Co: 40% de Sn
C β: 98% de Sn
Exercício Resolvido #4
Universidade Paulista- UNIP
Determine a proporção de cada fase do exercício anterior.
Passo 1
Vamos delimitar o traçado para as 2 temperaturas (linhas horizontais) e o teor de cobre (10%) com uma linha vertical.
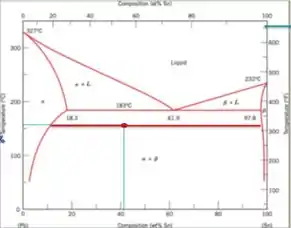
Passo 2
Utilizando as informações das fases presentes do exercício anterior podemos calcular a proporção apenas aplicando na fórmula.
E consequentemente temos o restante que falta para 100% da outra fase.
Resposta
Exercício Resolvido #5
Universidade Paulista- UNIP
Para a liga composta de ferro- carbono (Fe-C), determine a linha eutética e eutetóide.
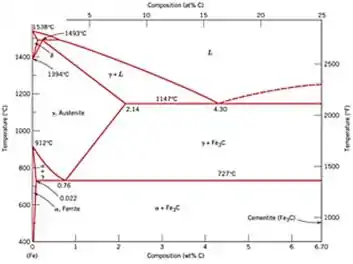
Passo 1
Primeiramente devemos determinar o ponto eutético no diagrama...
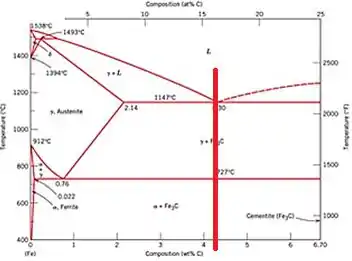
Traçando uma linha desde o ponto eutético e rebatendo na composição temos um teor de 4,3%C.
Passo 2
Agora devemos fazer o mesmo para o eutetóide, traçar uma reta do ponto e rebater na composição ...
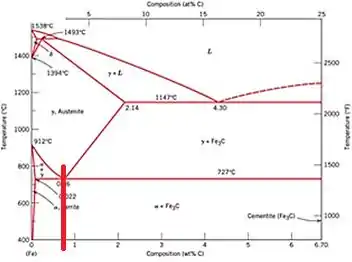
Rebatendo temos o teor de 0,76% C
Resposta
Ponto eutético: 4,3% C.
Eutetóide: 0,76% C
Exercício Resolvido #6
Universidade Paulista- UNIP
Para a liga composta de ferro- carbono (Fe-C), determine a temperatura eutética e eutetóide.
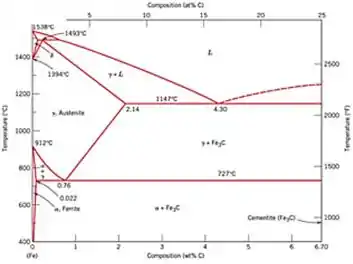
Passo 1
Primeiramente devemos determinar o ponto eutético no diagrama...
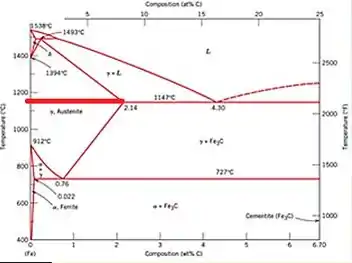
Traçando uma linha desde o ponto eutético e rebatendo no eixo da temperatura temos, 1148 °C.
Passo 2
Agora devemos fazer o mesmo para o eutetóide, traçar uma reta do ponto e rebater na temperatura ...
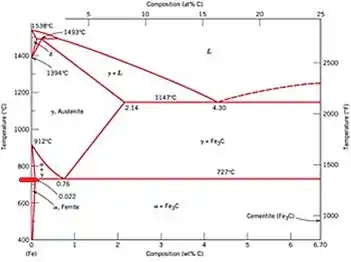
Rebatendo temos a temperatura de 727°C.
Resposta
Ponto eutético: 1148°C
Eutetóide: 727°C
Exercício Resolvido #7
Universidade Paulista- UNIP
Para a liga composta de ferro- carbono (Fe-C), determine a temperatura do início de solidificação desta liga e qual a primeira fase sólida que se solidifica a esta temperatura.
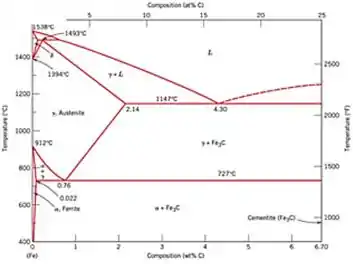
Passo 1
Primeiramente devemos determinar onde começa a solidificação, observa-se que o liquido vai se solubilizando com o γ (austenita).
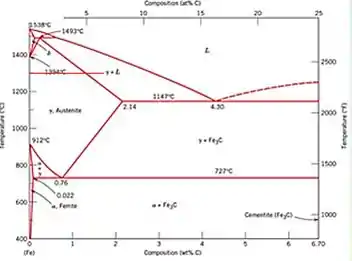
Resposta
A 1300°C
Primeira fase sólida austenita (γ).
Exercício Resolvido #8
HYPERLINK "https://www.qconcursos.com/questoes-de-concursos/provas/ufes-2014-ufes-tecnico-em-metalurgia" UFES - 2014 - Técnico em Metalurgia
Analise o diagrama Ferro-Carbono (Fe-C) abaixo.
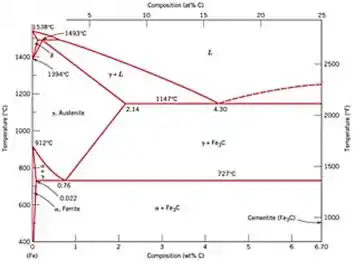
Com base no diagrama Ferro-Carbono (Fe-C), é CORRETO afirmar:
- A solubilidade máxima do carbono na austenita é de 0,76 % em peso.
- A reação eutética acontece com o carbono a 2,14 % em peso, logo, na fronteira do campo austenítico.
- A perlita é o resultado da transformação eutetoide
Passo 1
A solubilidade máxima do carbono na austenita é de 2,14 % em peso.
Passo 2
Reação eutética (ponto eutético ocorre para 4,3% C a 1147°C )
Passo 3
A perlita é o resultado da transformação eutetoide
Resposta
Alternativa 3