Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Mobilidade atômica

Ver Todos os Exercícios

Teoria

E aí, tudo bem?

A difusão ocorre da movimentação atômica aleatória e como eles se movem??? Veremos agorinhaa!!!

. Os mecanismos para que ocorra a movimentação átomica dependem da estrutura cristalina, dos tamanhos atômicos e da extensão dos defeitos nos cristaisA movimentação livre, leve e solta das partículas será impedido pelas partículas vizinhas, aff.. quando ocorre varias vezes seguidas, como cosequencia temos o deslocamento global específico de matéria. Na maioria dos sólidos, os átomos estão muito ligados às suas posições de equilíbrio. Poréémmm, devido às vibrações térmicas, alguns desses átomos se movem aleatoriamente ao longo da rede e um grande número destes movimentos podendo resultar num transporte significativo de material, por isso chamamos de movimento de difusão no estado sólido. 

Primeira Lei de Fick: Difusão no Estado Estacionário

A difusão é um processo que depende do tempo, e porque???????? o quão rápido ocorrerá a difusão, ou seja, a taxa de transferência de massa. Essa taxa é, com freqüência, expressa como um fluxo de difusão (J), definido como sendo a massa (M) que está em difusão através e perpendicularmente a uma área unitária de seção reta do sólido (A) por unidade de tempo (t). Resumindo, da essa equação:

J = M A t

As unidades para J são quilogramas ou átomos por metro quadrado por segundo (kg/m 2 -s ou átomos/m 2 -s).

Se o fluxo difusivo não variar ao longo do tempo, existe uma condição de estado estacionário. Para que o fluxo não varie com o tempo é necessário que também não varie com a posição.

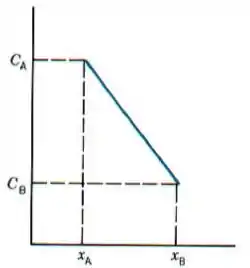
Notem que: C = f(x) é uma função linear de x.

Para processos de difusão em estado estacionário, a equação que correlaciona o fluxo de difusão J com o gradiente de concentração dC/dx é chamada de PRIMEIRA LEI DE FICK.

J = - D d C d X

Onde:

D: coeficiente de difusão

dC: variação de concentração

dX: variação de posição

E sabe porque do sinal negativo?

O sinal negativo na equação acima indica que o fluxo ocorre na direção contrária à do gradiente de concentração, isto é, no sentido das concentrações altas para as concentrações baixas (Ca – Cb).

Resumo deste rolê todo: A velocidade de transferência de um gás qualquer é proporcional a área e ao gradiente de pressão inversamente proporcional a espessura do sólido, deem uma espiadinha na figura aqui em baixo.

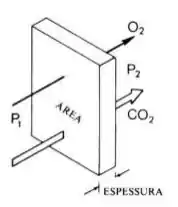
Vamos fazer um exemplo para uma boa compreensão?

Uma placa de zinco está exposta a 500°C a uma atmosfera rica em carbono em um dos lados, e pobre de carbono na outra face. Se o regime estacionário é alcançado, determine o fluxo de difusão do carbono através da placa, sendo a concentração de carbono estão na posição 0,1 e 0,2m abaixo da superficie são respectivamente 1,2 kg/m³ e 0,9 kg/m³ respectivamente. Considere o coeficiente de difusão de 1,6 x 10 -11 m²/s.

J = - D d C d X

J = - 1 , 6   x   10   - 11   m ² / s 0,9 - 1,2 k g / m ³ 0,2 - 0,1 m

J = - 1 , 6   x   10   - 11 m 2 s Χ   3 k g / m 4

J = - 1 , 6   x   10 - 11     m 2 s Χ -   3 k g / m 4

J = 4,8     x   10 - 11   k g / m 2 s

Sugiro a vocês sempre levarem as unidades juntos, para visualizar a unidade final :D

Segunda Lei de Fick-Difusão em estado não-estacionário

A maioria das situações práticas envolvendo difusão ocorre em condições de estado não-estacionário ou seja, o fluxo de difusão e o gradiente de concentração em um ponto específico no interior de um sólido variam ao longo do tempo, havendo como resultado um acúmulo ou esgotamento líquido do componente que se encontra em difusão.

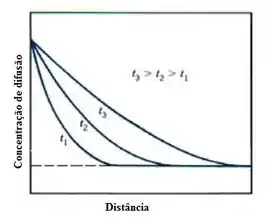
Notem na figura acima os perfis de concentração em três instantes de tempo diferentes do processo de difusão.

Uma solução na prática é aquela para um sólido com a concentração na superfície é mantida constante. Com freqüência, a fonte do componente que está se difundindo é uma fase gasosa, cuja pressão parcial é mantida em um valor constante. Veja as considerações que devemos conhecer:

  • Antes da difusão, todos os átomos do soluto presentes no sólido estão ali distribuídos uniformemente, mantendo uma concentração C0
  • O valor de x na superfície é zero e aumenta com a distância para dentro do sólido.
  • O tempo é tomado como sendo o instante imediatamente anterior ao início do processo de difusão.

Para t = 0, C = C0 em 0 ≤ x ≤ ∞

Para t > 0, C = Cs (a concentração superficial constante) em x = 0

A aplicação dessas condições de contorno nos da a equação alí debaixo:

C x - C o C s - C o = 1 - e r f ( x 2 D t )

Onde:

Cx: concentração a uma profundidade x após um tempo t

e r f ( x 2 D t ) : função de gauss, valores tabelados , geralmente fornecidos nos exercícios ;-)

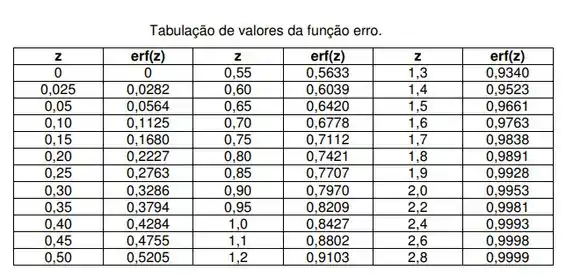
Vamos fazer um exemplo para entender?

Pretende-se cementar um aço com 0,1% C, mantendo-o em uma atmosfera com 1,2% C em uma elevada temperatura, até que se atinja 0,35% C em uma profundidade de 3 mm abaixo da superfície. Qual o tempo total de cementação se o coeficiente de difusão for D = 1,5x10 -11 m2 /s?

Vamos catar as informações dos problemas ?? Co = 0,1% C; Cs = 1,2% C; C(x,t) = 0,35% C; x = 3 mm = 0,003 m (importante deixar em metros)

0,35 - 0,1 1,2 - 0,1 = 1 - e r f ( x 2 D t )

1 - 0,38 = e r f ( x 2 D t )

0,68 = e r f ( x 2 D t )

Agora temos que usar a tabela acima, para um erf , 0,68 o erro (z) é de 0,7.

0,7 = ( 0,002 2 2 × 10 - 11 t )

0,7 × 2 = ( 0,002 2 × 10 - 11 t )

1,4 = ( 0,002 2 × 10 - 11 t )

1,4 × 2 × 10 - 11 t = 0,002

2 × 10 - 11 t = 0,002 / 1,4

2 × 10 - 11 t = 1,4 × 10 - 3   (agora temos que elevar ao quadrado dos lados, para cancelar a raiz e achar o t)

2 × 10 - 11 t = 1,96 × 10 - 6

t= 9800s passando para “horas” basta dividir por 3600

t= 27,22h

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

Os mecanismos para que ocorra a movimentação atômica dependem:

  1. Tamanho dos átomos
  2. Defeitos nos cristais
  3. Tipo de ligações

Determine:

  1. Apenas A
  2. A, B
  3. A, B, C
  4. Nenhuma das alternativas

Passo 1

Os mecanismos para que ocorra a movimentação atômica dependem da estrutura cristalina, dos tamanhos atômicos e da extensão dos defeitos nos cristais

Passo 2

Na maioria dos sólidos, os átomos estão muito ligados às suas posições de equilíbrio, devido às vibrações térmicas, alguns desses átomos se movem aleatoriamente ao longo da rede

Resposta

Alternativa II

Exercício Resolvido #2

Elaboração própria

Sobre a 1° lei de Fick determine a opção correta:

  1. Pode ser definida como a passagem de moléculas em conjunto através de um fluido por meio de um deslocamento em conjunto e desordenado das mesmas por um fluxo.
  2. Pode ser definida como a transferência de moléculas individuais através de um fluido por meio de um deslocamento individual e ordenado das mesmas por um fluxo.
  3. Quando o fluido se encontra inteiramente imóvel (estado estacionário), a difusão molecular ocorre devido ao gradiente de concentração.

Passo 1

Pode ser definida como a transferência (ou deslocamento) de moléculas individuais através de um fluido por meio de um deslocamento individual e desordenado das mesmas por um fluxo.

Resposta

Alternativa III

Exercício Resolvido #3

Elaboração própria

Uma placa de aço é exposta a 600   ° C em um ambiente rico em carbono, do outro lado um ambiente com baixo carbono. Se é atingido um regime estacionário, calcule o fluxo de difusão do carbono através de uma placa de prata, dado que as concentrações de carbono nas posições a 4 e 12   m m abaixo da superfície são 1,6 e 0,95   k g / m ³ , respectivamente. Considerando o coeficiente de difusão 2,21 ×   10 - 11   m ² / s .

Passo 1

Primeiramente temos que definir a fórmula

J = - D d C d X

Passo 2

Transformando as posições de m m para m :

4   m m × 1   m 1000   m m =   0 , 0 04 m

12   m m × 1   m 1000   m m =   0 , 0 12   m

J = ( - 2,21   x   10 - 11     m ² / s ) × 0,95 - 1,6   k g / m ³ 0 , 0 12 - 0 , 0 04   m

Fazendo primeiramente a divisão

J = ( - 2,21   x   10 - 11   m 2 / s )   × ( - 81 , 25   k g / m 4 )

J = 1,79     x   10 - 9   k g / m ² s

Resposta

J = 1,79     x   10 - 9   k g / m ² s

Exercício Resolvido #4

Elaboração própria

Uma solução contendo uma mistura gasosa e vapor d’água é pressurizada contra uma placa de alumínio de 4mm de espessura e área de 0,31   m ² a 325 ° C . O coeficiente de difusão é de 1,1 ×   10 - 8   m ² / s e a concentração do lado da placa de alta e baixa pressão é de 1,12 e 0,12   k g / m ³ . A difusão acontece em estado estacionário, calcule o fluxo de difusão em k g / h .

Passo 1

Primeiramente temos que definir a fórmula

J = - D d C d X

Passo 2

Transformando as posições de m m para m

4   m m 1   m 1000   m m =   0,0 0 4 m

J = - 1,1   x   10 - 8 m 2 / s ×   0,12 - 1,12   k g / m ³ 0,004   m

Fazendo primeiramente a divisão

J = - 1,1   x   10 - 8   m 2 s × ( - 250   k g / m 4 )

J = 2,75     x   10 - 6   k g / m ² s

Passo 3

Passando J = 2,75     x   10 - 6   k g / m ² s

Para kg/h é necessário multiplicar pela área.

J = 2,75   x   10 - 6   k g m 2 s × 0,31 m 2 = 8,52   x   10 - 7 k g / s

1h=60 min=3600s

J = 8,52   x   10 - 7 k g s × 3600   s = 3,07   x   10 - 3 k g / h  

Resposta

J = 3,06   x   10 - 3 k g / h  

Exercício Resolvido #5

Elaboração própria

Para cementar uma engrenagem de aço com 0,2%C a uma atmosfera de 1,6%C em uma elevada temperatura, até que se atinja 0,35%C em uma profundidade de 1,1 mm abaixo da superfície. Determine o período total de cementação quando o coeficiente de difusão for de 2x 10 -7 m²/s.

Passo 1

Primeiramente temos que definir a fórmula, para isso devemos interpretar o problema. O exercício não fala em regime estacionário e também o processo de cementação não é obtido um gradiente de concentração linear. Assim sendo necessário utilizar a 2° Lei de fick.

C x - C o C s - C o = 1 - e r f ( x 2 D t )

Passo 2

Aplicando na formula.

0,35 - 0,2 1,6 - 0,2 = 1 - e r f ( x 2 D t )

0,107 = 1 - e r f ( x 2 D t )

0,107 - 1 = - e r f ( x 2 D t ) (Multiplicando por -1)

0,8928 = e r f ( x 2 D t )

Agora temos o valor erro (erf) onde z =   e r f ( x 2 D t ) , vale 0,89. Então deve-se consultar a tabela do valor erro para determinar “z”.

Passo 3

Consultando a tabela, nota-se que o valor encontra-se entre z= (1,1 – 1,2).

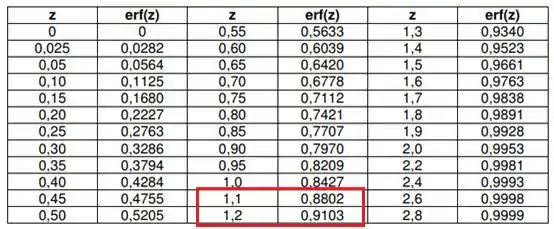
Sabendo que:

Z1= 1,1 -> erf ⁡ z = 0,8802

Z -> erf ⁡ z = 0,8928

Z2= 1,2 -> erf ⁡ z = 0,9103

z - z 1 z 2 - z 1 = e - e 1 e 2 - e 1

z - 1,1 1,2 - 1,1 = 0,8928 - 0,8802 0,9103 - 0,8802

Z= 1,1418

z = x 2 D t

1,1418 = 1,1   x   10 - 3 2 2 x   10 - 7 t

Para acharmos o t devemos elevar ao quadrado os dois lados para remover a raiz

( 1,1418 ) ² = ( 1,1   x   10 - 3 2 2 x   10 - 7 t ) ²

1,3037 t = 1,375

T= 1,054 x   10 3 segundos

Sabendo que 1h= 3600s

T= 0,292h

Resposta

T= 0,292h

Exercício Resolvido #6

Elaboração Própria

Classifique em ordem decrescente as magnitudes dos coeficientes de difusão para os seguintes sistemas:

  1. N no Fe a 700°C
  2. Cr no Fe a 700°C
  3. N no Fe a 900°C

Temos:

  1. A,b,c
  2. C,b,a
  3. C,a,b

Passo 1

Primeiramente devemos determinar o raio atômico dos elementos do N, Fe e Cr e são respectivamente: 0,065 nm, 0,124 nm e 0,125 nm.

Passo 2

Quanto maior for a temperatura maior será o coeficiente de difusão, e quanto menor o diâmetro então temos:

N no Fe a 900°C

N no Fe a 700°C

Cr no Fe a 700°C

Resposta

Alternativa III

Exercício Resolvido #7

Elaboração Própria

O coeficiente de difusão do cobre no alumínio a 300ºC e 520ºC são respectivamente 3,21 X10-11 e de 2,21 X 10-12 m2 /s. Determine o tempo aproximado a 300ºC que determinará o mesmo efeito de difusão em termos de concentração de cobre em um ponto no alumínio análogo a 8 h de tratamento térmico a 520ºC.

Passo 1

Na mesma posição teremos a mesma concentração de cobre, logo x é constante.

C x - C o C s - C o = 1 - e r f ( x 2 D t )

Passo 2

Para ambas temperaturas temos:

D300°C t300°C= D520°C t520°C

t300°C= D520°C t520°C/ D300°C

t300°C= (3,21 X10-11) x 8 / 2,21 X 10-12

t300°C= 116,2 h

Resposta

t300°C= 116,2 h

Exercício Resolvido #8

Elaboração Própria

Avalie a Lei de Fick para a difusão molecular de um componente numa mistura binaria e assinale a alternativa correta:

  1. A Lei de Fick institui que a densidade de fluxo de massa por difusão molecular é inteiramente proporcional ao gradiente de concentração do componente
  2. A Lei de Fick institui que a densidade de fluxo de massa por difusão molecular não depende do gradiente de concentração do componente
  3. A Lei de Fick estabelece que a densidade de fluxo de massa por difusão molecular de um componente é inversamente proporcional ao gradiente de concentração do componente

Passo 1

A Lei de Fick institui que a densidade de fluxo de massa por difusão molecular é inteiramente proporcional ao gradiente de concentração do componente

Passo 2

Então temos a equação matemática

J = -D (dC/dx)

Resposta

Alternativa A

Exercício Resolvido #9

CALLISTER, Ciências dos materiais, 8° edição, cap.5, Nº 11

Determine o tempo de carbonetação necessário para atingir uma concentração de carbono de 0,45%p a 2mm da superfície de uma liga ferro-carbono contendo inicialmente 0,2%pC. A concentração deve ser mantida em 1,3%pC e o tratamento deve ser conduzido a 1000°C. Considere os dados de difusão para Fe y na tabela 5.2.

Passo 1

C x - C o C s - C o = 1 - e r f x 2 D t

0,45 - 0,2 1,3 - 0,20 = 0,227 = 1 - e r f x 2 D t

0,227 = 1 - e r f x 2 D t

e r f x 2 D t = 1 - 0,227 = 0,7727

Passo 2

Interpolando conforme a tabela 5.2 podemos ter:

Z - 0,85 0 , 90 - 0,85 = 0,7727 - 0,7707 0,797 - 0,7707

Z = 0,854 = x 2 D t

A 1000°C (1273K) temos:

D = 2,3 × 10 - 5 e x p   148000 8,31 × 1273  

D = 1,93 × 10 - 11   m 2 / s

Passo 3

Agora sim podemos determinar o tempo, substituindo na fórmula os valores encontrados.

0,854 = x 2 D t

0,854 = 2 × 1 0 - 3   2 1,93 × 10 - 11   t

0,854 × 2 = 2 × 10 - 3   1,93 × 10 - 11   t

1,708 × 1,93 × 10 - 11   t = 2 × 10 - 3  

1,93 × 10 - 11   t = 2 × 10 - 3   / 1,708

Elevando ao quadrado os dois lados podemos retirar a raiz o que facilitará os cálculos:

( 1,93 × 10 - 11   t ) ² = ( 1,17 × 10 - 3   ) ²  

1,93 × 10 - 11   t = 1,37 × 10 - 6  

t = 7,1 × 10 4   s   o u   19,7 h  

Resposta

T= 19,7h

Exercício Resolvido #10

Capítulo 5 , Perguntas e Problemas, exercício 1 4

Considere um par de difusão composto por dois sólidos semi-infinitos do mesmo metal e que cada lado do par de difusão possui uma concentração diferente do mesmo elemento de impureza; além disso, considere que cada nível de impureza seja constante em todo o seu lado do par de difusão. Para essa situação, a solução para a segunda lei de Fick (assumindo que o coeficiente de difusão para a impureza seja independente da concentração) é a seguinte:

C x = C 1 + C 2 2 - C 1 - C 2 2 erf ⁡ x 2 D t

( 5.15 )

Nessa expressão, quando a posição x = 0 é tomada como interface inicial do par de difusão, então C 1 é a concentração de impurezas para x < 0 ; de maneira análoga, C 2 é o teor de impurezas para x > 0 .

É formado um par de difusão composto por duas ligas prata-ouro é formado; essas ligas possuem composições de 98 % p A g - 2 % p A u e 95 % p A g - 5 % p A u . Determine o tempo em que este par de difusão deve ser aquecido a 750 ° C   ( 1023   K ) para que a composição seja de 2,5 % p A u na posição a 50   μ m no interior no lado do par de difusão contendo 2 % p A u . Os valores para a constante pré-exponencial e para a energia de ativação para a difusão do A u na A g são de 8,5 × 10 - 5   m 2 / s e 202.100   J / m o l , respectivamente.

Passo 1

Olá! Tudo bem? Neste exercício, devemos determinar o tempo de difusão a 750 ° C   que fornecerá uma composição de 2,5 % p A u na posição a 50   μ m no interior no lado do par de difusão contendo 2 % p A u . Assim, para esse problema, a Equação 5.15 assume a forma:

2,5 = 5 + 2 2 - 5 - 2 2 erf ⁡ 50 × 10 - 6   m 2 D t

Passo 2

Agora é necessário calcular o coeficiente de difusão a 750 ° C ( 1023   K ) , dado que D 0 = 8,5 × 10 - 5   m 2 / s e Q d = 202100   J / m o l . Da equação 5.8 (pág. 112 ; 8 ª Ed.), temos:

D = D 0 exp ⁡ - Q d R T

D = 8,5 × 10 - 5 m 2 s exp ⁡ - 202.100   J / m o l ( 8,31   J / m o l - K ) ( 1023   K )  

D = 4,03 × 10 - 15   m 2 / s

Passo 3

Agora, devemos substituir o valor encontrado no Passo 2 na equação 5.15 :

2,5 = 5 + 2 2 - 5 - 2 2 erf ⁡ 50 × 10 - 6   m 2 ( 4,03 × 10 - 15   m 2 / s ) ( t )

0,6667 = erf ⁡ 393,8 s t

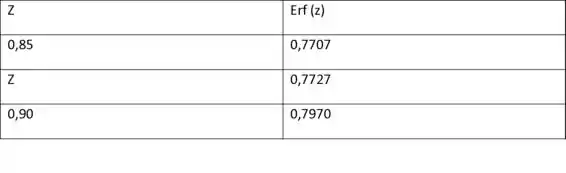
Usando os dados da Tabela 5.1 , na pág. 110, é necessário determinar o valor de z para o qual a função de erro é 0,6667 . Para isso, usamos a interpolação linear da seguinte maneira:

        z                            erf ⁡ z

0 , 650                       0 , 6420

        y                               0,6667

0 , 700                     0 , 6778

y - 0,650 0,700 - 0,650 = 0 , 6667 - 0,6420   0,6778 - 0,6420

y = 0 , 6844

Após acharmos o valor de y = z , podemos encontrar t :

y = 0,6844 = 393,8 s t

t = 3,31 × 10 5   s = 92   h

Resposta

92   h

Exercícios de Livros Relacionados

Explique sucintamente a diferença entre autodifusão e interdifusão.
O nitrogênio de uma fase gasosa deve ser difundir no ferro puro a 700 ° C . Se a concentração na superfície for mantida em 0,1 % p N, qual será a concentração a 1m m da superfície após 1 0h ? O coefic
Cite os valores dos coeficientes de difusão para a interdifusão de carbono tanto no ferro α (CCC) quanto no ferro γ (CFC) a 900 ° C . Qual valor é maior? Explique por que isso acontece.
Uma liga ferro-carbono com estrutura cristalina CFC contendo inicialmente 0,35 % p C está exposta a uma atmosfera rica em oxigênio e virtualmente isenta de carbono a 1400K ( 1127 ° C ). Sob essas circ
Determine o tempo de carbonetação necessário para atingir uma concentração de carbono de 0,45%p a 2mm da superfície de uma liga ferro-carbono contendo inicialmente 0,2%pC. A concentração deve ser mant