Ensaios de tenacidade à fratura
Produzido por Erick PinhoTeoria
E aiiiiii galera!!!!
No tópico anterior vimos que a tenacidade à fratura é uma propriedade fundamental e importante dos materiais. Vimos que um material pode resistir a uma trinca sem ocorrer uma fratura frágil desde que o valor de seja menor do que , chamado tenacidade à fratura.
Como conseguimos obter esses valores de tenacidade à fratura,?

Bom, ai é que entra os ensaios a fim de descobrirmos esses valores para cada material!
Corpos de prova
Há diversos ensaios padronizados, diferentes, para medir os valores de tenacidade à fratura dos materiais. Nos Estados Unidos, esses ensaios são normatizados pela ASTM. As normas estabelecem todo o procedimento para o ensaio, bem como o tamanho e a geometria do corpo de prova. Para cada ensaio o corpo de prova (com tamanho e geometria especificados) contém um defeito preexistente, geralmente uma trinca afiada que foi introduzida. O dispositivo de ensaio aplica uma carga sobre o corpo de provas, em uma taxa especificada, e também mede os valores para a carga e o deslocamento da trinca.
A figura abaixo é um esquema representativo da forma de aplicação de carregamento para os corpos de prova de tenacidade à fratura dos tipos: a) C(T) - compacto e b) SE(B) – corpo de prova de dobramento em três apoios .
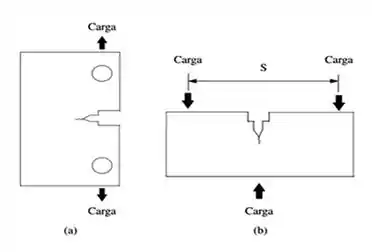
Há várias geometrias de corpos de prova: compacto, dobramento, em forma de disco, em forma de arco, entre outros.
Não se preocupem com esses formatos, pois, com dito, todos estão especificados em normas como, por exemplo, a ASTM E399 e BS 5447.

Procedimento dos Ensaios
O primeiro passo para executar um ensaio de é determinar as dimensões críticas do corpo de prova. Essas dimensões são obtidas através de equações presentes na norma.
O segundo passo é a seleção do corpo de prova, dentre os vários tipos disponíveis. Os mais utilizados são: corpos de prova de dobramento em três apoios [SE(B)] e compacto [C(T)].
O terceiro passo é executar a pré-trinca de fadiga. Não se preocupe em saber como isso é feito, somente tenha em mente que a trinca de fadiga é considerada a mais aguda que se pode conseguir em um laboratório, por isso o entalhe usinado em forma de V é estendido por fadiga.
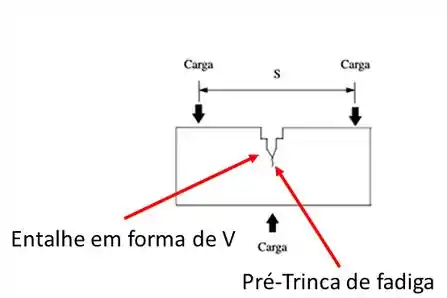
O quarto passo é aplicação de uma força crescente com a aquisição da curva “carga vs deslocamento da abertura da trinca ”.
O próximo passo, após a fratura, é medir a pré-trinca na linha central, na metade da distância entre linha central e as bordas, e nas bordas.
Por fim, análise do gráfico carga versus deslocamento para determinação do .
Vamos praticar uma pouco?
Corpos de prova
Procedimento dos Ensaios
Exercícios Resolvidos
Exercício Resolvido #1
Concurso CPTM – Engenheiro de Manutenção - 2012
Sobre a tenacidade de um material, assinale a alternativa correta.
- Determina a resistência à fratura de um material.
- É uma medida da resistência de um material a uma deformação plástica localizada.
- É a deformação plástica que ocorre num material, sob tensão constante ou quase constante, em função do tempo.
- É o efeito observado em estruturas com estado de tensões bem abaixo da tensão de ruptura, quando se pode desenvolver um acúmulo do dano com cargas cíclicas continuadas, conduzindo a uma falha do componente ou estrutura.
- É a deformação elástica que ocorre num material
Passo 1
Tenacidade à fatura é uma propriedade que mede a resistência de um material a uma fratura frágil quando uma trinca está presente
Resposta
Letra: a)
Exercício Resolvido #2
Elaboração própria
A respeito da tenacidade a fratura, assinale a questão correta.
- A tenacidade à fratura é uma propriedade que mede a resistência de um material a uma fratura ductil quando uma trinca está presente.
- Os materiais frágeis possuem alta tenacidade à fratura e são vulneráveis a falhas catastróficas.
- A tenacidade à fratura diminui com a diminuição da temperatura.
- A tenacidade à fratura aumenta com o aumento da taxa de deformação.
- O aumento da tensão de escoamento aumenta a tenacidade à fratura.
Passo 1
Em destaque segue os erros:
- A tenacidade à fratura é uma propriedade que mede a resistência de um material a uma fratura frágil quando uma trinca está presente.
- Os materiais frágeis possuem baixa tenacidade à fratura e são vulneráveis a falhas catastróficas.
d) A tenacidade à fratura diminui com o aumento da taxa de deformação.
- O aumento da tensão de escoamento diminui a tenacidade à fratura.
Resposta
Letra: c)
Exercício Resolvido #3
Elaboração própria
Atraves do ensaio de tenacidade à fratura consegui-se obter a seguinte propriedade:
- Limite de escoamento
- Tensão de ruptura
- Coeficiente de Poisson
Passo 1
O ensaio de tenacidade à fratura é realizado a fim de obtermos o valor da tenacidade à fratura em deformação plana
Resposta
Letra: c)
Exercício Resolvido #4
Elaboração própria
Sobre o ensaio de tenacidade a fratura é correto afirmar:
- Um corpo de prova cilíndrico é submetido a um esforço de tração até a ruptura.
- Sobre o corpo de prova é aplicado uma força, através de uma esfera, e medido a área da impressão feita pela esfera.
- Corpos de prova padronizados são submetidos a esforços repetidos ou flutuantes , e estes podem romper-se com uma carga bem inferior à carga máxima atingida na tração.
- Corpo de prova entalhado tendo uma pré-trinca causada por fadiga e solicitado a tensões de carregamento em tração ou flexão. Como resultado do ensaio, obtém-se um gráfico relacionando a carga aplicada e o deslocamento da abertura do entalhe.
Passo 1
Na letra (a) temos a descrição do ensaio de tração, na (b) ensaio de dureza, na (c) ensaio de fadiga e na (d) ensaio de tenacidade a fratura.
Resposta
Letra: d)
Exercício Resolvido #5
Elaboração própria
O valor da tenacidade à fratura em deformação plana significa:
- A resistência à propagação da trinca.
- A resistência à ruptura.
- A resistência ao impacto.
- A resistência a penetração.
Passo 1
O valor da tenacidade à fratura em deformação plana significa a resistência à propagação da trinca em condições severas de triaxialidade de tensões, em ambiente neutro e com níveis de crescimento da trinca , para o caso de deformações plásticas pequenas.
Resposta
Letra: a)
Exercício Resolvido #6
Elaboração Própria
Cite 3 fatores que podem fazer com que um metal apresente uma transição dúctil-frágil.
Passo 1
Fala ai! Três fatores que podem fazer com que um metal apresente uma transição dúctil-frágil são:
- Exposição a tensões sob temperaturas relativamente baixas
- Taxas de deformação elevadas
- Presença de um entalhe afilado
Resposta
- Exposição a tensões sob temperaturas relativamente baixas
- Taxas de deformação elevadas
- Presença de um entalhe afilado
Exercício Resolvido #7
Elaboração Própria
Como a temperatura da transição dúctil-frágil pode ser reduzida em aços de baixa resistência?
Passo 1
Fala ai! Para aços de baixa resistência, a temperatura da transição dútil-frágil é sensível à composição da liga e também à micro estrutura. Tanto a diminuição no tamanho de grão, quanto o aumento no teor de carbono podem melhorar as propriedades mecânicas desses aços.
Resposta
Para aços de baixa resistência, a temperatura da transição dútil-frágil pode ser reduzida pela diminuição no tamanho de grão e pela redução no teor de carbono.
Exercício Resolvido #8
Livro Callister, Problema 8.12
Encontram-se tabulados a seguir os dados coletados a partir de diversos ensaios de impactos Charpy em um ferro fundido nodular.
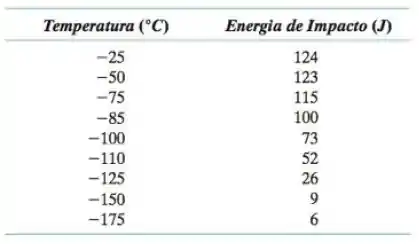
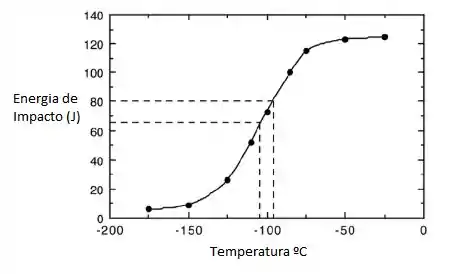
- Trace os dados na forma da energia de impacto em função da temperatura.
- Determine a temperatura de transição dúctil-frágil como a temperatura correspondente à média entre as energias de impacto máxima e mínima.
- Determine a temperatura de transição dúctil-frágil como a temperatura na qual a energia de impacto é de 80J.
Passo 1
Na letra a:
O gráfico da energia de impacto versus temperatura é mostrado abaixo.
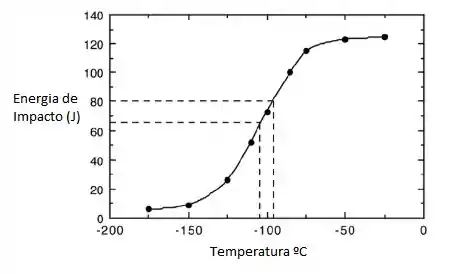
Passo 2
Na letra b:
A média das energias de impacto máxima e mínima dos dados é
Conforme indicado no gráfico pelo conjunto de linhas tracejadas, a temperatura de transição dúctil para quebradiça de acordo com este critério é de cerca de –105 ° C.
Passo 3
Na letra c:
Além disso, conforme observado no gráfico pelo outro conjunto de linhas tracejadas, a temperatura de transição dúctil para quebradiça para uma energia de impacto de 80 J é de cerca de –95 ° C.
Resposta
- –95 ° C
Exercício Resolvido #9
Livro Callister, Problema 8.13
Encontram-se tabulados a seguir os dados coletados a partir de diversos ensaios de impactos Charpy em um aço 4140 revenido.
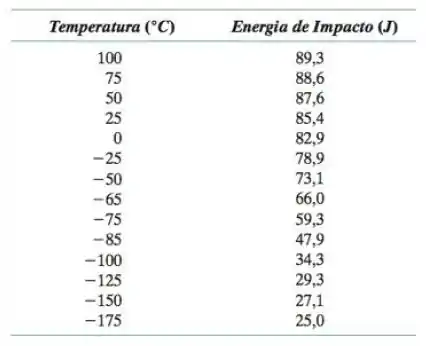
- Trace os dados na forma da energia de impacto em função da temperatura.
- Determine a temperatura de transição dúctil-frágil como a temperatura correspondente à média entre as energias de impacto máxima e mínima.
- Determine a temperatura de transição dúctil-frágil como a temperatura na qual a energia de impacto é de 70J.
Passo 1
O gráfico da energia de impacto versus temperatura é mostrado abaixo.
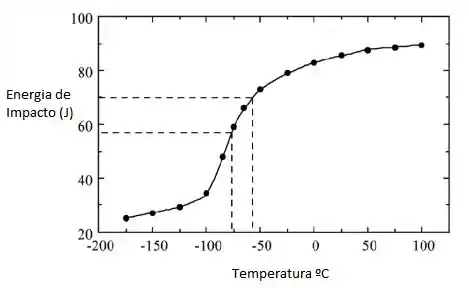
Passo 2
Na letra b:
A média das energias de impacto máxima e mínima dos dados é
Conforme indicado no gráfico pelo conjunto de linhas tracejadas, a temperatura de transição dúctil para quebradiça de acordo com este critério é de cerca de –75 ° C.
Passo 3
Na letra c:
Além disso, conforme observado no gráfico pelo outro conjunto de linhas tracejadas, a temperatura de transição dúctil para quebradiça para uma energia de impacto de 70 J é de cerca de –55 ° C.
Resposta
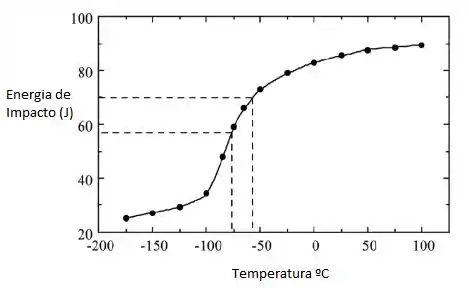
- –55 ° C
Exercício Resolvido #10
Elaboração própria
Para que o ensaio de tenacidade à fratura em deformação plana possa ser validado sugeri utilizar a expressão abaixo:
em que é a espessura do corpo de prova, o comprimento da trinca em uma superfície, o valores de tenacidade a fratura em deformação plana e a limite de escoamento.
Ensaia-se um aço-carbono com e limite de escoamento igual a
Um corpo de prova com uma espessura de e comprimento de trinca igual a . Essas duas dimensões são válidas para o ensaio?
Passo 1
Vamos primeiramente calcular os valores de e validos a partir da equação dada:
Passo 2
Agora devemos comparar se os valores de e são maiores ou iguais ao calculado:
Note que tanto a espessura quanto o comprimento da trinca satisfazem a expressão, logo a espessura de e o comprimento da trinca de são condições validas para o ensaio.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #11
Elaboração própria
Para que o ensaio de tenacidade à fratura em deformação plana possa ser validado sugeri utilizar a expressão abaixo:
em que é a espessura do corpo de prova, o comprimento da trinca em uma superfície, o valores de tenacidade a fratura em deformação plana e a limite de escoamento.
Ensaia-se o aço 4340 temperado e revenido a 425°C com e limite de escoamento igual a
Um corpo de prova com uma espessura de e comprimento de trinca igual a . Essas duas dimensões são válidas para o ensaio?
Passo 1
Vamos primeiramente calcular os valores de e validos a partir da equação dada:
Passo 2
Agora devemos comparar se os valores de e são maiores ou iguais ao calculado:
Note que tanto a espessura quanto o comprimento da trinca satisfazem a expressão, logo a espessura de e o comprimento da trinca de 3 são condições validas para o ensaio.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #12
Garcia, A. Et al. Ensaios do Materiais, 2º edição
Um componente mecânico de grandes dimensões deve ser fabricado com ligas de alumínio, de diferentes propriedades mecânicas finais. A liga 2024-T351 apresentou limite de escoamento e tenacidade à fratura de , ao passo que a liga 7075-T651 apresentou e . Pergunta-se:
a) Se a espessura das chapas é de , ter-se-á condição de deformação plana?
b) Em caso afirmativo, qual será o tamanho da trinca se for admitida uma tensão de trabalho de e Y=1?
Dica: Utilize as equações abaixo.
Passo 1
Primeiramente vamos checar se a condição de deformação plana é validada pela equação abaixo:
Passo 2
Dados fornecidas para:
- liga 2024-T351
- liga 7075-T651
e
e
Passo 3
Para descobrirmos o tamanho trinca critica para uma tensão de trabalho de e , vamos utilizando a equação abaixo com os dados da liga que é valida para a condição de deformação plana:
No caso da liga 2024-T351, não se tem deformação plana, já que sua espessura é muito pequena e ela deve ser aumentada para valores acima de para que isso não ocorra. Para a liga 7075-T651, admitindo-se uma tensão de trabalho menor que, pode- se trabalhar com trincas com comprimento inferior a .
Resposta
Ei, a resposta está no passo a passo :)