Tenacidade à fratura
Produzido por Erick PinhoTeoria
Fala pessoal! Tudo tranquilo?
Quando estudamos as propriedades dos materiais vimos que tenacidade é um termo mecânico que pode ser usado em vários contextos.
Tenacidade
Uma maneira de definimos tenacidade é uma propriedade que indica o quanto o material resiste à fratura quando uma trinca (ou outro defeito concentrador de tensões) está presente. A essa tenacidade damos o nome de tenacidade à fratura.
Porém, é importante diferenciarmos de outras tenacidades. Por exemplo, uma maneira de definirmos a tenacidade é como a habilidade de um material absorver energia e se deformar plasticamente antes de fraturar. Outro exemplo é para condições de carregamento dinâmico (elevada taxa de deformação) e quando um entalhe (ou ponto de concentrador de tensões) está presente, a tenacidade ao entalhe é averiguada por meio de um ensaio de impacto.
Outra maneira de definirmos tenacidade, para situação estática (pequena taxa de deformação), uma medida da tenacidade nos metais (inferida a partir da deformação plástica) pode ser determinada a partir dos resultados de um ensaio tensão-deformação em tração. Neste caso a tenacidade será a área abaixo da curva tensão versus deformação até o ponto da fratura.

Agora que entendemos as várias maneiras de definirmos tenacidade, vamos estudar a tenacidade à fratura!

Tenacidade à Fratura
Se a carga aplicada a um material contendo uma trinca é demasiadamente elevada, a trinca pode crescer de repente e fazer com que o membro falhe por fratura de forma frágil, isto é, apresentando uma pequena deformação plástica, mesmo para materiais capazes de grandes quantidades de deformação plástica, como aço de baixo carbono e ligas de alumínio dúcteis.
Como vimos no tópico anterior, a partir da teoria da mecânica da fratura, pode ser definida uma quantidade útil, chamado fator de concentrador de tensões, . Especificamente, é uma medida da severidade da presença de uma trinca e é afetada pela dimensão da trinca, a tensão e a geometria.
Certo material pode resistir a uma trinca sem ocorrer uma fratura frágil, enquanto o valor de é inferior a um valor crítico , chamado tenacidade à fratura.
Onde, é um parâmetro ou função adimensional que depende tanto do tamanho quanto da geometria da trinca e da amostra, assim como do modo de aplicação da carga, é a tensão crítica para a propagação de uma trinca e é o comprimento da trinca.
Modo de Abertura (Deformação Plana)
Em amostras relativamente finas, o valor de dependerá da espessura da amostra. Entretanto, quando a espessura da amostra é muito maior que as dimensões da trinca, o valor de torna-se independente da espessura; sob tais condições existe uma condição de estado plano de deformações. Este estado é caracterizado por não haver deformação perpendicular ��s faces.

Logo, o valor de para essa situação de amostra espessa é conhecido como tenacidade à fratura em deformação plana. Assim, o valor de recebe o subscrito , . Esse subscrito indica o modo de deslocamento da superfície de uma trinca, que no caso da deformação plana é o modo (modo de abertura ou de tração). Esse modo consiste simplesmente na separação das faces da trinca.
Modos de Deslizamento e Rasgamento
Há mais dois modos: modo , ou modo de deslizamento, as faces da trinca deslizam-se relativamente uma na outra numa direção perpendicular à frente da trinca e modo , ou modo de rasgamento, também envolve o deslizamento relativo das faces da trinca, mas agora a direção é paralela à frente da trinca.

Vimos que nos materiais dúcteis há uma deformação plástica apreciável na frente de uma trinca que está avançando. Essa deformação faz com que materiais dúcteis tenham valores de relativamente grandes. Por outro lado, materiais frágeis, por não terem essa deformação apreciável, possuem baixos valores de e são vulneráveis a falhas catastróficas.
A tenacidade à fratura em deformação plana, , é uma propriedade fundamental dos materiais; ela depende de muitos fatores, entre os quais os de maior influência são a temperatura, a taxa de deformação e a microestrutura. Quanto maior for a taxa de deformação menor será a magnitude do . O oposto ocorrerá com a diminuição da temperatura, ou seja, essa diminuição causará uma diminuição da magnitude do .
Vamos praticar uma pouco?
Tenacidade à Fratura
Modo de Abertura (Deformação Plana)
Modos de Deslizamento e Rasgamento
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
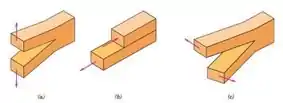
Quais são os 3 modos de deslocamento da superfície de uma trinca?
Passo 1
Fala ai! Os 3 modos de deslocamento de uma trinca são:
- Modo de abertura ou de tração
- Modo de cisalhamento
- Modo de rasgamento
E pra gente visualizar melhor:
Resposta
- Modo de abertura ou de tração
- Modo de cisalhamento
- Modo de rasgamento
Exercício Resolvido #2
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição
Um componente de uma aeronave é fabricado em uma liga de alumínio que possui uma tenacidade à fratura em deformação plana de 35 MPa. Foi determinado que a fratura ocorre em uma tensão de 250 Mpa quando o comprimento máximo (ou critico) de uma trinca interna é de 2,0 mm. Para esse mesmo componente e essa mesma liga, ocorrerá fratura sob um nível de tensão de 325 Mpa, quando o comprimento máximo de uma trinca for de 1,0 mm? Por que sim, ou pro que não?
Passo 1
Os dados fornecidos são:
Passo 2
Através dos dados fornecidos podemos calcular o parâmetro de escala , através da equação abaixo:
Passo 3
Agora que temos o parâmetro de escala , vamos calcular para o nível de tensão de 325Mpa e uma trinca interna de 1,0 mm:
Para o tamanho de trinca interna de 1,0 mm a tensão critica é de 353 Mpa, como a tensão imposto foi de 325Mpa, portanto menor do que a tensão critica, logo não ocorrerá a fratura do material.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição
Suponha que um componente da asa de um avião seja fabricado em uma liga de alumínio com uma tenacidade à fratura em deformação plana de 40 MPa. Foi determinado que a fratura ocorre em uma tensão de 365 Mpa quando o comprimento máximo (ou critico) de uma trinca interna é de 2,5 mm. Para esse mesmo componente e essa mesma liga, calcule o nível de tensão no qual a fratura ocorrerá para um comprimento critico de trinca interna de 4,0 mm.
Passo 1
Os dados fornecidos são:
Passo 2
Através dos dados fornecidos podemos calcular o parâmetro de escala , através da equação abaixo:
Passo 3
Agora que temos o parâmetro de escala , vamos o nível de tensão no qual a fratura ocorrerá com uma trinca interna de 4,0 mm:
Assim, a tensão critica para uma trinca interna de 4,0 mm é de 288 Mpa.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição
Uma grande chapa é fabricada em aço, que possui uma tenacidade à fratura em deformação plana de 55 . Se, durante seu uso em serviço, a chapa fica exposta a uma tensão de tração de 200 determine o comprimento mínimo de uma trinca superficial que levará à fratura. Assuma um valor de 1,0 para Y.
Passo 1
Os dados fornecidos são:
Passo 2
Através dos dados fornecidos e considerando que a tensão dada seja a tensão critica podemos calcular o comprimento minino da trinca superficial, através da equação abaixo:
Resposta
Exercício Resolvido #5
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição
Calcule o comprimento máximo admissível para uma trinca interna em um componente feito de uma liga de alumínio 7075-T651 com tenacidade à fratura em deformação plana de 24 , que está submetido a uma tensão equivalente à metade do seu limite de escoamento. Admita que o valor de Y seja de 1,35. Considere o limite de escoamento como sendo 495 Mpa.
Passo 1
Os dados fornecidos são:
Passo 2
Através dos dados fornecidos e considerando que a tensão dada seja a tensão critica podemos calcular o comprimento minino da trinca interna, através da equação abaixo:
Multiplicando os dois lados por 2, a fim de determinarmos o tamanho da trinca interna:
Resposta
Exercício Resolvido #6
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição
Um componente estrutural na forma de uma chapa com grande largura deve ser fabricado em aço que possui uma tenacidade à fratura em deformação plana de 77,0 e um limite de escoamento de 1400 MPa O limite de resolução do tamanho de defeito do aparelho de detecção de defeitos é de 4,0 mm. Se a tensão de projeto é de metade do limite de escoamento e se o valor de Y é de 1,0, determine se um defeito crítico para essa chapa está ou não sujeito a detecção.
Passo 1
Os dados fornecidos são:
Passo 2
Através dos dados fornecidos e considerando que a tensão dada seja a tensão critica podemos calcular o comprimento minino da trinca interna, através da equação abaixo:
Portanto, para uma trinca superficial critica a resolução do aparelho não detectaria o defeito. Porem, para trincas internas o aparelho detectaria o defeito antes da falha, uma vez que para trinca interna o tamanho critico é de 7,7mm.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Lista USP – PMT 2200
Um aço tem um limite de escoamento de 1100 MPa, um limite de resistência de 1200
MPa e uma tenacidade à fratura de 90 . Considere
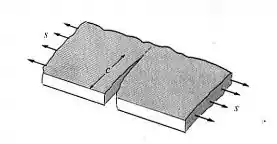
a) Uma placa com a configuração da figura abaixo, tem uma trinca passante de 2mm de comprimento. Ela vai quebrar antes de escoar ou escoar antes de quebrar?
b)Qual é o tamanho máximo de trinca que pode estar presente sem que a chapa frature antes de deformar?
Passo 1
Os dados fornecidos são:
Passo 2
Letra a)
Vamos calcular a tensão critica para os dados fornecidos:
Como a tensão critica está abaixo da tensão de escoamento o material irá fraturar antes de escoar.
Passo 3
Letra b)
Para que a placa fratura antes de deformar vamos considerar que a tensão critica seja de 1100MPa. Assim:
Obs.: Caso desejamos arredondar o valor para dois algarismo significativos devemos truncar o valor, pois caso arrendondemos para cima teremos um comprimento de trinca maior do que é possivel o comprimento critico. Logo:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
Prova IDECAN - 2017
A fratura simples é a separação de um corpo em duas ou mais partes em resposta à imposição de tensões ou variações de temperatura. Para a engenharia de materiais, é possível distinguir uma fratura em frágil ou dúctil. Acerca do processo de fratura, é correto afirmar que:
- a fratura frágil é caracterizada por uma extensa deformação plástica na região em que a trinca se propaga, de maneira relativamente lenta. No caso de fratura dúctil, as trincas se propagam de modo rápido e são acompanhadas de pouca deformação plástica.
- materiais frágeis apresentam pequenas trincas e defeitos de distintos tamanhos, geometrias e orientações. Quando a tensão de tração na extremidade de um desses defeitos excede o valor da tensão crítica, ocorre a formação de uma trinca que se propaga resultando na fratura.
- a tenacidade à fratura é a propriedade que mede a resistência de um material à fratura frágil, quando este possui uma trinca. A magnitude da tenacidade à fratura em deformação plana aumenta com o aumento da taxa de deformação e com a diminuição da temperatura.
- Charpy e Izod são técnicas de ensaio por impacto para determinar as características de fraturas dos materiais. No ensaio Izod, o corpo de prova tem um entalhe central e é apoiado em ambas as extremidades. No ensaio Chary, o corpo é engastado em um lado e recebe o impacto na outra extremidade.
Passo 1
Letra a)
A fratura dúctil é caracterizada por uma extensa deformação plástica na região em que a trinca se propaga, de maneira relativamente lenta. No caso de fratura frágil, as trincas se propagam de modo rápido e são acompanhadas de pouca deformação plástica.
Letra c)
A tenacidade à fratura é a propriedade que mede a resistência de um material à fratura frágil, quando este possui uma trinca. A magnitude da tenacidade à fratura em deformação plana diminui com o aumento da taxa de deformação e com a diminuição da temperatura
Letra d)
Charpy e Izod são técnicas de ensaio por impacto para determinar as características de fraturas dos materiais. No ensaio Charpy, o corpo de prova tem um entalhe central e é apoiado em ambas as extremidades. No ensaio Izod, o corpo é engastado em um lado e recebe o impacto na outra extremidade
Resposta
Letra: b)
Exercício Resolvido #9
Livro Callister, Problema 8.11
Após consultar outras referências, escreva um relatório sucinto sobre uma ou duas técnicas de ensaios não destrutivos usadas para detectar e medir defeitos internos e/ou superficiais em ligas metálicas.
Passo 1
Aqui, vou falar rapidamente sobre dois ensaios não destrutivos:
Líquido Penetrante
O ensaio por Líquidos Penetrante é um dos melhores métodos para a detecção de descontinuidades superficiais de materiais isentos de porosidade. Também são utilizados para a detecção de vazamentos em tubos, tanques, soldas e componentes. Para aplicar o líquido é usado um pincel (ou algo do tipo). Depois de aplicado, o líquido age por um tempo de penetração. Depois de remover o penetrante do produto por meio de lavagem com água ou remoção com solventes, um revelador (talco) mostra a localização das descontinuidades superficiais com precisão.
Passo 2
Partículas Magnéticas
Usando esse método, podemos detectar defeitos de trincas, junta fria, inclusões, gota fria, dupla laminação, falta de penetração, dobramentos, segregações, entre outros. O método está baseado na geração de um campo magnético que percorre toda a superfície do material. As linhas magnéticas do fluxo induzido no material desviam-se de sua trajetória ao encontrar uma descontinuidade superficial ou sub superficial, criando assim uma região com polaridade magnética, altamente atrativa a partículas. No momento em que se provoca esta magnetização na peça, aplica-se as partículas magnéticas por sobre a peça que será atraída à localidade da superfície que conter uma descontinuidade formando assim uma clara indicação de defeito.
Para que as descontinuidades sejam detectadas é importante que elas estejam de tal forma que sejam “interceptadas” ou “cruzadas” pelas linhas do fluxo magnético induzido.
Resposta
O aluno deverá pesquisar sobre os END (Ensaios Não Destrutivos).
Exercício Resolvido #10
Elaboração Própria
Descreva sucintamente o que é ?
Passo 1
Fala ai! O é o símbolo pra tenacidade à fratura. É uma propriedade que mede a resistência de um material a uma fratura frágil quando tem uma trinca.
O é descrito pela seguinte expressão:
Onde Y é um parâmetro adimensional que depende do tamanho e da geometria da trinca, é a tensão crítica pra propagação da trinca e é o comprimento da trinca.
Resposta
O é o símbolo pra tenacidade à fratura,uma propriedade que mede a resistência de um material a uma fratura frágil quando tem uma trinca, descrito pela seguinte expressão:
Exercício Resolvido #11
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição
Um corpo de provas de aço 4340, com uma tenacidade à fratura em deformação plana de 45 MPa, está exposto a uma tensão de 1000Mpa. Esse corpo de provas sofrerá fratura, sabendo-se que a maior trinca superficial existente possui o comprimento de 0,75 mm? Por que sim, ou por que não? Assuma que o valor do parâmetro seja 1,0.
Passo 1
Os dados fornecidos são:
Passo 2
O problema nós pergunta se o corpo de prova sofrerá fratura quando a maior trinca superficial for 0,75mm. Para isso devemos calcular a tensão critica e comparar com a tensão que o corpo de prova está exposto.
Em que é a tensão critica e é a tensão que o corpo de prova está exposto.
Como, a tensão critica é menor do que a tensão imposta, o corpo de prova irá sofrer a fratura.
Resposta
Ei, a resposta está no passo a passo :)