Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Nucleação homogênea

Ver Todos os Exercícios

Teoria

E aí galerinha.

Vimos nos tópicos de diagramas de fases que quando uma liga está em seu estado líquido e começamos a resfriar essa liga atingimos a linha l i q u i d u s , onde nossa liga começa o processo de solidificação, ou seja, começa a aparecer os primeiros cristais sólidos. No diagrama abaixo vemos a linha l i q u i d u s

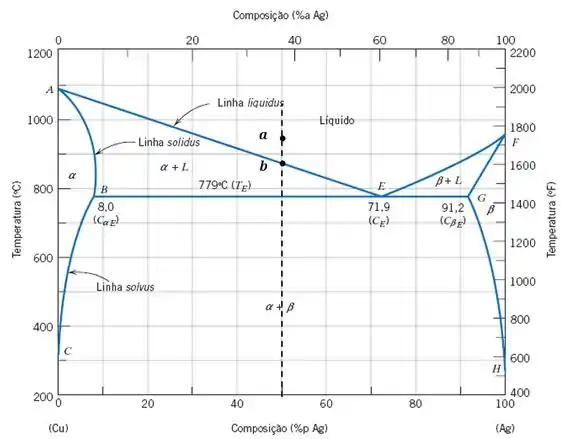
No ponto a nossa liga estará 100 % líquida, ao atingir o ponto b começa a surgir os primeiros cristais, conforme figura abaixo.

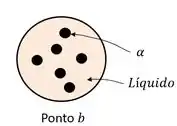
À medida que continuamos a diminuir a temperatura esses cristais sólidos crescem até formarem todo o sólido.

Assim, teremos duas etapas na transformação de fases: a nucleação, onde surgem os primeiros cristais e o crescimento, onde os cristais crescem.

Nucleação homogênea

A nucleação irá ocorrer de acordo com a energia livre de Gibbs (G), segundo a equação abaixo:

∆ G = ∆ H - T ∙ ∆ S

Em que, ∆ G é a variação da energia livre de Gibbs, ∆ H é a variação da entalpia, T é a temperatura e ∆ S é a variação da entropia.

Vimos, e não custa relembrar, que sempre que temos a variação da energia de Gibbs negativa teremos uma reação espontânea.

∆ G < 0 → r e a ç ã o   e s p o n t â n e a

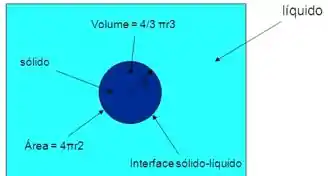
Vimos que a nucleação está relacionada com a energia livre, agora vamos pensar na nucleação do nosso primeiro cristal sólido, conforme figura abaixo, e imagine que nosso sólido formado seja uma esfera.

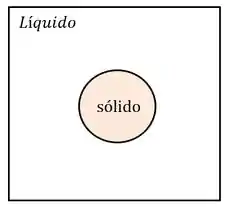
Sabemos que o volume da esfera é:

V = 4 3 π r 3

E que a área superficial da esfera é:

S = 4 π r 2

Ou seja, existe duas energias associadas com a nucleação homogênea de um primeiro cristal. Em primeiro lugar teremos um ∆ G relacionado com o volume da esfera.

∆ G v o l u m e

Para temperatura abaixo da linha l i q u i d u s significa que meu ∆ G v o l u m e para transformação do material para sólido é negativo.

∆ G v o l u m e < 0

À medida que o volume cresce a área superficial da esfera também aumenta, ou seja, existem uma variação da energia de Gibbs associada a essa superfície (tensão superficial), porém a variação da energia de Gibbs para a superfície é sempre maior do que zero.

∆ G s u p e r f i c i e γ > 0

Quando juntamos os dois termos: ∆ G v o l u m e e ∆ G s u p e r f i c i e . Teremos o ∆ G da nucleação homogênea.

∆ G = - 4 3 π r 3 ∆ G v o l u m e + 4 π r 2 γ

Fazendo um gráfico do ∆ G em função do raio da esfera:

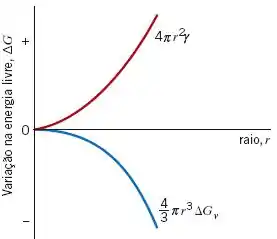
Analisando o gráfico somente para a energia de superfície nota-se que não é espontâneo crescer, pois aumenta a energia livre. Enquanto que para a energia de volume para temperatura abaixo da l i q u i d u s é cada vez mais negativa, ou seja, espontânea.

Agora plotando um gráfico somando as duas energias teremos uma curva que cresce no inicio até um ponto máximo e depois decresce, conforme figura abaixo.

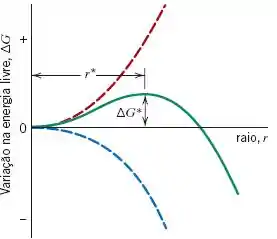
Nesse ponto máximo, teremos o nosso ∆ G * , variação de energia crítica e o nosso r * , raio crítico.

Raio crítico e energia de Gibbs crítica

Quando nosso sólido passa do tamanho do raio crítico a reação é espontânea e nosso sólido não para de crescer.

Para calcularmos o raio crítico vamos utilizar a equação abaixo:

∆ G = - 4 3 π r 3 ∆ G v o l u m e + 4 π r 2 γ

Para calcularmos o raio crítico devemos calcular a derivada da equação acima e iguala-la a zero:

d ∆ G d r = 0

d ∆ G d r = - 4 π r * 2 ∆ G v o l u m e + 8 π r * γ

r * - 4 π r * ∆ G v o l u m e + 8 π γ = 0

- 4 π r * ∆ G v o l u m e + 8 π γ = 0

- 4 π r * ∆ G v o l u m e = - 8 π γ

r * = 2 γ ∆ G v o l u m e

Para calcularmos a variação de energia crítica, basta substituir o raio crítico na equação:

∆ G * = - 4 3 π 2 γ ∆ G v o l u m e 3 ∆ G v o l u m e + 4 π 2 γ ∆ G v o l u m e 2 γ

∆ G * = - 4 3 π 8 γ 3 ∆ G v o l u m e 3 ∆ G v o l u m e + 4 π 4 γ 3 ∆ G v o l u m e 2

∆ G * = - 32 3 π γ 3 ∆ G v o l u m e 2 + 16 π γ 3 ∆ G v o l u m e 2

∆ G * = - 32 π γ 3 + 48 π γ 3 3 ∆ G v o l u m e 2 = 16 π γ 3 3 ∆ G v o l u m e 2

Uma outra expressão da energia livre de Gibbs para o volume é:

∆ G v o l u m e = ∆ H f T f - T T f

Em que ∆ H f é o calor latente de fusão e T f é a temperatura de fusão. A partir dessa expressão podemos ver a dependência do ∆ G v o l u m e em função da temperatura, ou seja, se tivermos uma temperatura mais alta do que a temperatura de fusão teremos um raio crítico maior e consequentemente maior energia livre será necessário.

Bora praticar para fixar!

Nucleação homogênea

Raio crítico e energia de Gibbs crítica

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

Defina nucleação homogênea.

Passo 1

Quando resfriamos um material que está na fase líquida ele não vira sólido todo de uma vez. A primeira etapa do processo de transformação de fase é a nucleação!

A nucleação nada mais é do que a formação de embriões de fase sólida no meio da fase líquida.

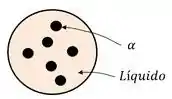
Quando esse núcleo sólido se forma no meio de uma matriz contínua, chamamos essa nucleação de nucleação homogênea!

Resposta

Os núcleos da nova fase se formam de maneira uniforme ao longo de toda a fase original.

Exercício Resolvido #2

Elaboração própria

Descreva como ocorre a nucleação homogênea

Passo 1

Quando resfriamos um material que está na fase líquida ele não vira sólido todo de uma vez. A primeira etapa do processo de transformação de fase é a nucleação!

A nucleação nada mais é do que a formação de embriões de fase sólida no meio da fase líquida.

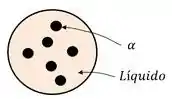
Quando esse núcleo sólido se forma no meio de uma matriz contínua, chamamos essa nucleação de nucleação homogênea!

Passo 2

A fase sólida nucleia na fase liquida sem que ocorra a contribuição energética de elementos no sistema metal líquido/metal sólido, como superfícies e interfaces.

Resposta

A nucleação homogênea é a formação de embriões de fase sólida no meio de fase líquida contínua, sem que ocorra a contribuição energética de elementos no sistema metal líquido/metal sólido, como superfícies e interfaces.

Exercício Resolvido #3

Elaboração própria

Sobre os embriões da fase sólida da nucleação, determine a alternativa correta:

  1. Regiões com ordenação de longo alcance
  2. Os embriões eventualmente se tornam instáveis
  3. A estabilidade dos embriões dependem do tamanho crítico e das condições térmicas na fase liquida.

Passo 1

Primeiro vamos relembrar o que é a nucleação homogênea!

Quando o material vai mudar de fase, ou seja, passar da fase líquida pra fase sólida, primeiro a gente tem a formação do que a gente chama de embriões da fase sólida!

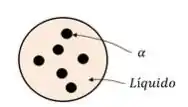
Esses embriões nada mais são do que cristais beeem pequenininhos de sólido que vão crescendo com o tempo, até o material se transformar todo.

Passo 2

Vamos analisar as alternativas então!

  1. Regiões com ordenação de longo alcance

    2. Na verdade, os embriões são regiões com ordenação de curto alcance, justamente por serem muito pequenos!

  2. Os embriões eventualmente se tornam instáveis

    3. O que acontece é justamente o contrário! Os embriões surgem de uma instabilidade, quando o consumo de energia daquela região passa a ser menor, e, portanto, mais favorável, na fase sólida. Eventualmente os embriões se tornam estáveis.

    Passo 3

  3. A estabilidade dos embriões depende do tamanho crítico e das condições térmicas na fase liquida.

Essa é a nossa alternativa certa! Mas por que?

Conforme esses cristais de fase sólida vão crescendo, uma hora esse crescimento passa a ser espontâneo. O raio crítico, que faz a virada entre o crescimento forçado e o crescimento espontâneo é determinado pelas seguintes expressões:

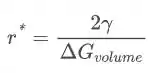
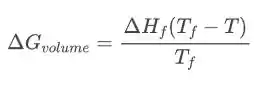
Portanto a estabilidade depende sim da temperatura.

Resposta

Alternativa 3

Exercício Resolvido #4

Elaboração própria

Interprete o gráfico a seguir:

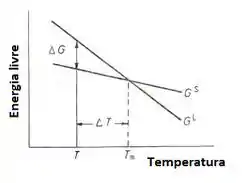
Passo 1

Curvas de energia livre das fases líquida e sólida de um metal hipotético, representando a estabilidade de ambas em torno do ponto de fusão do material.

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #5

Elaboração própria

Determine a alternativa correta a respeito do núcleo:

  1. Núcleo crítico: núcleo com o tamanho máximo para continuar o crescimento
  2. Núcleo subcrítico: núcleos menores que os núcleos críticos produzidos por flutuações
  3. Ocorre o surgimento dos átomos do sólido a partir dos núcleos críticos.

Passo 1

Núcleo crítico: núcleo com o tamanho mínimo para continuar o crescimento

Passo 2

Núcleo subcrítico: núcleos menores que os núcleos críticos produzidos por flutuações

Passo 3

Não ocorre o surgimento dos átomos do sólido a partir dos núcleos subcríticos.

Resposta

Alternativa B

Exercício Resolvido #6

Elaboração própria

Explique sucintamente o gráfico abaixo que é a representação da variação do tamanho do raio crítico do núcleo em função do grau de super-resfriamento para o cobre.

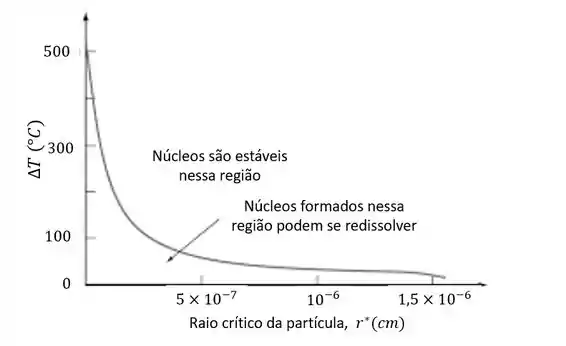
Passo 1

No gráfico é possível observar o tamanho mínimo dos embriões (passiveis de nucleação e crescimento) diminui conforme ocorre o aumento do super-resfriamento.

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #7

Elaboração própria

Analise as equações abaixo em relação ao raio crítico e a energia de ativação, explique o que é possível concluir observando-as.

r * = - 2 γ T f Δ H f 2 1 T f - T

Δ G * = 16 π γ 3 T f 2 3 Δ H f 2 1 T f - T

Passo 1

É possível concluir que o raio crítico e a energia de ativação diminuem com a temperatura. Importante ressaltar que quando ocorre a redução da temperatura a nucleação passa ser mais imediata.

Resposta

É possível concluir que o raio crítico e a energia de ativação diminuem com a temperatura.

Exercício Resolvido #8

Elaboração própria

Ao processo de nucleação que ocorre a partir de uma fase homogênea se dá o nome de nucleação homogênea. Na nucleação homogênea a partícula pode ser nucleada em qualquer ponto do sistema, pois não existem sítios preferenciais para a nucleação. Defina as variáveis que influenciam neste processo.

Passo 1

  • Forma da partícula (esférica simples)

  • Velocidade de nucleação

Resposta

A forma da partícula e a velocidade de nucleação.