Um corpo de massa com velocidade de de módulo, que se move sobre uma superfície horizontal, choca-se frontalmente com a extremidade livre de uma mola ideal de constante elástica .
Qual a compressão máxima sofrida pela mola?
Passo 1
Faaaaaaala aí! Vamo que vamo pra cima de mais uma questão sobre Conservação de Energia.
Primeiro vamos fazer um desenho para entender o que está acontecendo
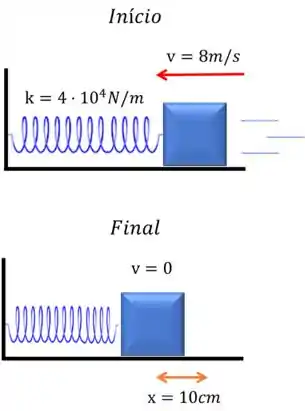
Vamos considerar que a energia mecânica é conservada, ou seja, ela permanece constante, então temos que:
E a energia mecânica é a soma das energias cinética com a potencial de um corpo em certo momento
E só lembrando aqui rapidinho, temos que a energia cinética é dada por
E a energia potencial é separada pela energia potencial gravitacional e a energia potencial elástica.
Cada uma delas é calculada desse jeitinho aqui
Show, agora que já relembramos uns conceitos importantes vamos começar de fato o problema.
OBS: Podemos usar a energia potencial tanto com a letra quanto com , cada livro escreve de uma forma e cada professor escolhe a que acha melhor. Aqui usaremos sempre a notação com , ok? 😊
Passo 2
Vamos começar olhando a energia mecânica inicial. Sabemos que no início
Como aqui não temos diferença de altura e ainda não chegamos na mola, vamos ter apenas a energia cinética, então
E como a energia cinética é , temos que
Substituindo pelos valores que tiramos do enunciado, ficamos com:
Faremos primeiro a potência
Simplificando ficamos com:
Passo 3
Show de bolinhas, agora vamos pra cima da energia mecânica final.
Ele pede a compressão máxima sofrida pela mola. Isso acontece quando a velocidade é igual a zero. Porque é exatamente o momento em que o corpo para de comprimir a mola e começa a voltar.
Então, como não temos variação de altura e nem velocidade, a energia mecânica final será apenas a elástica
Isso quer dizer que
Substituindo por , temos
Simplificando temos:
Passo 4
Belezinha, como a gente já viu nessa questão, a energia mecânica se conserva, ou seja,
Como queremos achar a energia cinética quando o corpo chega ao solo, só precisamos igualar as energias mecânicas que achamos!
Igualando, temos que
Passando o dividindo, temos que
Simplificando, ficamos com
Agora, aplicando a raiz quadrada, vamos ter que
Tirando a raiz quadrada do numerador e do denominador, teremos
Vamos ter então
Isso nos dá
Que também podemos escrever como
Resposta
ou