Verifique se o conjunto de funções dadas é linearmente independente. Caso seja linearmente dependente, determine a relação de dependência entre elas.
Passo 1
Opa! Tudo bem?
Para determinar a relação de dependência entre as funções, precisamos calcular o wronskiano. E para isso, vamos precisar determinar as derivadas de:
Como todas as funções são polinômios vamos usar a Regra do Tombo e termos as seguintes derivadas:
Mas temos funções, e como isso a matriz que iremos precisar pra determinar o wronskiano deverá ser uma matriz . Assim, precisaremos também das derivadas de segunda ordem:
Com isso em mãos, vamos montar o wronskiano da seguinte forma:
Substituindo teremos:
Passo 2
O cálculo do wronskiano é dado pelo determinante dessa matriz. Para calcular esse determinante, vamos copiar as duas primeiras colunas ao lado da matriz multiplicar os elementos na diagonal descendo, como no esquema:
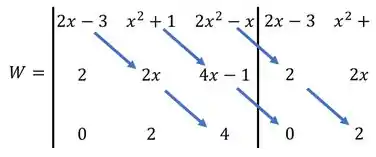
Somamos cada multiplicação, ficando com:
Que será:
Guardamos essa parte.
E depois multiplicamos as diagonais subindo, desta forma:
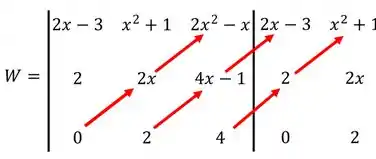
Essas multiplicações serão subtraídas:
Tirando os parênteses e arrumando os sinais:
Agora, nós juntamos as duas partes e teremos o nosso determinante wronskiano:
Simplificando...
Que é
O wronskiano é diferente de 0. Quando isso acontece nós concluímos que as funções são linearmente independentes.
E prontinho!
Resposta
O sistema é Linearmente Independente, pois