Teoria
E aí, beleza? Agora vamos aprender uma coisa que vai nos facilitar muito, muito mesmo, que é o fasor. Mas o que é isso?
Fasor é um número complexo que representa a amplitude e a fase de uma senóide. Ou seja, podemos, por exemplo, expressar a tensão simplesmente assim:
Viu só? Muito mais simples do que aquelas expressões com senos e cossenos.
Mas temos que ter o cuidado com duas coisas: a tensão ou a corrente têm que estar expressas em cosseno e a frequência tem que ser a mesma para todo o circuito, o que geralmente acontece, para podermos usar a representação fasorial.
Por exemplo, vamos escrever a corrente na forma fasorial.
Nosso primeiro passo é expressar a corrente em cosseno. Como
Logo,
Então, a forma fasorial de é
Forma retangular, polar e exponencial
Como o fasor é um número complexo, vamos ver as formas de representá-lo. Podemos representar um número complexo de três maneiras.
- Forma retangular:
- Forma polar:
- Forma exponencial:
Onde , é a parte real e é a parte imaginária de .
Onde é o módulo e é o ângulo de fase.
As formas polar e retangular se relacionam como na figura abaixo:
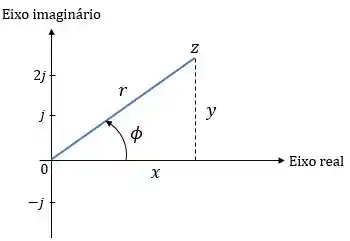
Portanto, sabendo e , podemos determinar e fazendo
Ou, se conhecemos e , podemos obter e fazendo
Essas relações são muito importantes, porque geralmente para operações de adição e subtração nós utilizamos a forma retangular, enquanto que em multiplicação e divisão utilizamos a forma polar.
Portanto, dependendo do exercício, vamos precisar transformar o fasor de uma forma para outra e vamos fazer isso utilizando essas relações.
Operações com número complexo
Vamos ver como funcionam as operações em números complexos que mais utilizaremos daqui em diante. Para isso, vamos supor que temos dois números complexos genéricos:
Adição:
Subtração:
Multiplicação:
Divisão:
Recíproco:
Raiz quadrada:
Conjugado Complexo:
Para você entender melhor, vamos determinar o número complexo dado pela expressão:
Transformando para forma retangular:
Substituindo,
Fazendo a adição no numerador e sabendo que é igual a , temos
Para efetuar a divisão precisamos passar os números para forma polar:
Portanto,
Diagrama fasorial
Em alguns exercícios pode ser pedido o diagrama fasorial, mas não é preciso se desesperar. Esse diagrama nada mais é do que a representação gráfica dos fasores.
Por exemplo, vamos fazer o digrama fasorial dos fasores e .
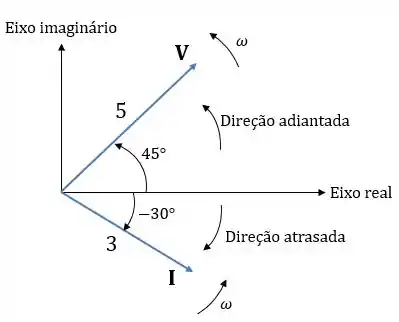
Como podemos ver, os fasores são como vetores e por isso são representados por uma letra maiúscula em negrito. Eles apresentam módulo e “direção”, que no caso é o ângulo de fase do fasor.
Além disso, em um mesmo circuito, eles apresentam a mesma frequência angular, ou seja, é como se ambos tivessem a mesma rotação de . Por isso, a representação em forma de fasor é dita como a representação no domínio da frequência.
Então a gente tem as seguintes representações:
Agora é a hora de praticar bastante para fixar o que se aprendeu.
Forma retangular, polar e exponencial
Operações com número complexo
Diagrama fasorial
Exercícios Resolvidos
Exercício Resolvido #1
Livro Sadiku, p.361, Problema 9.11
Determine os fasores correspondentes aos seguintes sinais:
Passo 1
Nesse exercício temos que transformar cada sinal para forma fasorial, aquela com módulo e ângulo. Para isso, temos que lembrar que os sinas têm que estar expressos em cossenos.
Passo 2
Na letra , temos . Como podemos ver a tensão já está expressa em cosseno. Então podemos passar para forma fasorial diretamente.
Passo 3
Na letra , a corrente está expressa em termos de seno: . Então, nosso primeiro passo é expressá-la em cosseno.
Como, , temos:
Agora é só escrever na forma fasorial.
Passo 4
Na letra , a tensão também está expressa em termos de seno. Vamos expressá-la em cosseno.
Como, , temos:
Agora é só escrever na forma fasorial.
Passo 5
Na letra , temos . Como podemos ver, a corrente já está expressa em cosseno, mas com sinal negativo. Para deixarmos com sinal positivo, basta somarmos ou subtrairmos no argumento do cosseno:
Agora, podemos passar para forma fasorial diretamente.
Resposta
Exercício Resolvido #2
Livro Sadiku, p.361, Problema 9.18
Obtenha as senoides correspondentes a cada um dos seguintes fasores:
Passo 1
Na letra , o fasor já está na forma polar. Então, podemos obter a expressão no domínio do tempo diretamente. Como ,
Passo 2
Na letra , o fasor está na forma retangular. Então, vamos passá-lo para forma polar:
Agora, podemos escrever a expressão no domínio do tempo. Sabendo que , temos:
Passo 3
Na letra , o fasor está na forma exponencial:
Desta forma, já conhecemos e .
Portanto, como , temos a seguinte senoide:
Resposta
Exercício Resolvido #3
Livro Sadiku, p.361, Problema 9.17
Duas tensões, e , aparecem em série de modo que sua soma é . Se e , determine .
Passo 1
Para determinar , vamos encontrar o seu fasor , porque no domínio do tempo é complicado somarmos e já que são senoides defasadas e com amplitudes diferentes. Então nosso primeiro passo é encontrar os fasores de e :
É importante ressaltar que só podemos fazer isso porque e possuem a mesma frequência angular:
Passo 2
Agora, vamos passar os fasores para forma retangular para efetuarmos a soma.
Somando e encontramos :
Passo 3
Para voltarmos para o domínio do tempo, primeiro temos que passar para forma polar:
Agora que temos o fasor na forma polar podemos voltar para o domínio do tempo e encontrar . Como , temos:
Resposta
Exercício Resolvido #4
Elaboração própria
Dada uma rede onde a tensão é e a frequência 60Hz. Converta para o domínio do tempo.
Passo 1
Bom o primeiro passo é descobrir a frequência angular :
Passo 2
Agora já podemos montar a expressão:
Resposta
Exercício Resolvido #5
Livro Sadiku, p.361, Problema 9.8
Calcule os números complexos a seguir e expresse seus resultados na forma retangular:
Passo 1
Sempre que vamos trabalhar com números complexos temos que ter em mente que nas operações de adição e subtração nós utilizamos a forma retangular, enquanto nas de multiplicação e divisão utilizamos a forma polar.
Passo 2
Na letra , o primeiro passo é passar para forma polar:
Substituindo e efetuando a divisão, temos:
Passo 3
Agora, temos que passar para forma retangular para efetuarmos a soma.
Substituindo e somando os números complexos, temos:
Passo 4
Na letra , o primeiro passo é passar para forma polar:
Substituindo e efetuando a multiplicação, temos:
Passo 5
Agora, temos que passar para forma retangular para efetuarmos a soma.
Substituindo e somando os números complexos, temos:
Resposta
Exercício Resolvido #6
Livro Sadiku, p.361, Problema 9.9
Calcule os números complexos a seguir e deixe seus resultados na forma polar:
Passo 1
Sempre que vamos trabalhar com números complexos temos que ter em mente que nas operações de adição e subtração nós utilizamos a forma retangular, enquanto nas de multiplicação e divisão utilizamos a forma polar.
Passo 2
Na letra , o primeiro passo é passar para forma polar:
Substituindo e efetuando a divisão, temos:
Passo 3
Agora, temos que passar para forma retangular para efetuarmos a soma que está dentro dos parênteses.
Substituindo e somando os números complexos, temos:
Passo 4
Agora é só passar para forma polar e efetuar a multiplicação.
Lembrando que na multiplicação de fasores a gente multiplica os módulos e soma os ângulos, temos:
Passo 5
Na letra , podemos efetuar as operações no numerador e denominador diretamente, já que os números complexos estão na forma certa para cada operação.
Passo 6
Agora é só passar para forma polar e efetuar a divisão. Mas quando a parte real do número complexo é negativa, é melhor colocarmos o sinal de menos em evidência e passarmos o que está dentro do parêntese para forma polar.
Logo, lembrando do sinal de menos:
Para deixarmos o módulo do fasor positivo podemos somar ou subtrair . Nesse caso, vamos somar , mas tanto faz mesmo. Portanto,
Passo 7
Lembrando que na divisão de fasores a gente divide os módulos e subtrai os ângulos, temos:
Resposta
Exercício Resolvido #7
Livro Sadiku, p.361, Problema 9.12
Seja e . Calcule as quantidades a seguir e expresse seus resultados na forma polar:
Passo 1
O enunciado nos forneceu os fasores e na forma polar. Como vimos na teoria, nas operações de adição e subtração nós utilizamos a forma retangular, enquanto que na multiplicação e divisão utilizamos a forma polar.
Então, vamos passar os fasores para forma retangular, porque dessa forma teremos eles expressos das duas formas e poderemos efetuar qualquer operação.
Passo 2
Transformando e para forma retangular:
Além disso, precisamos do conjugado de . Para isso, basta colocarmos o sinal negativo no ângulo:
Passo 3
Agora vamos partir para os cálculos. Na letra , temos:
Passo 4
Agora, precisamos passar para forma polar antes efetuar a multiplicação.
Portanto,
Agora, basta multiplicar os módulos e somar os ângulos:
Passo 5
Na letra , temos:
Para encontrarmos o conjugado na forma retangular basta inverter o sinal da parte imaginária:
Quando a parte real do número complexo é negativa, é melhor colocarmos o sinal de menos em evidência e passarmos o que está dentro dos parênteses para forma polar.
Então, vamos passar para forma polar.
Logo, lembrando do sinal de menos:
Para deixarmos o módulo do fasor positivo podemos somar ou subtrair . Nesse caso, vamos subtrair . Portanto,
Passo 6
Na letra , temos:
Agora, precisamos passar para forma polar antes efetuar a multiplicação.
Portanto,
Agora, basta dividir os módulos e subtrair os ângulos:
Resposta
Exercício Resolvido #8
Livro Sadiku, p.361, Problema 9.19
Usando fasores, determine:
Passo 1
No domínio do tempo é complicado efetuarmos essas operações, já que são senoides defasadas e com amplitudes diferentes. Então, utilizaremos fasores para efetuarmos essas contas. É importante ressaltar que para podemos fazer isso é necessário que a frequência seja a mesma.
Passo 2
Na letra , temos:
Como as duas parcelas estão escritas em termo de cosseno, podemos transformá-los diretamente para fasores:
Passo 3
Agora, para efetuarmos essa subtração precisamos passar os dois fasores para forma retangular:
Efetuando a subtração, temos:
Passo 4
Para voltarmos para o domínio do tempo, primeiro temos que passar o resultado que encontramos para forma polar:
Não podemos esquecer do sinal de menos. Logo,
Para deixarmos o módulo do fasor positivo podemos somar ou subtrair . Nesse caso, vamos somar . Portanto,
Agora que temos o fasor na forma polar podemos voltar para o domínio do tempo. Como , temos:
Passo 5
Na letra , precisamos escrever todas as parcelas em termos de cosseno antes de transformá-las para fasores. Então,
Portanto, temos a seguinte expressão com todas as parcelas escritas em termos de cosseno:
Passo 6
Agora, vamos escrever a expressão na forma fasorial.
Para efetuar essas somas precisamos passar cada fasor para forma retangular:
Quando temos o ângulo de ou , passamos de uma forma para outra rapidamente, sem efetuar conta.
Isso ocorre porque se o fasor tem um desses ângulos ele só possui componente no eixo imaginário do plano complexo. Se for ele estará na parte negativa, logo na sua forma retangular terá apenas parte imaginária negativa . Já se for sua forma retangular terá apenas parte imaginária positiva .
Passo 7
Agora sim podemos efetuar as operações.
Para voltarmos para o domínio do tempo, primeiro temos que passar para forma polar:
Agora que temos o fasor na forma polar podemos voltar para o domínio do tempo. Como , temos:
Resposta
Exercício Resolvido #9
Elaboração própria
Quando duas resistências estão em paralelo, nós realizamos a resistência equivalente ao realizar o seguinte procedimento:
Assim, faça o mesmo com os seguintes valores:
Descubra .
Passo 1
Primeiro de tudo, vamos realizar a soma entre esses dois fasores:
Passo 2
Como não conseguimos multiplicar dois fasores que estão na forma retangular, vamos transformar para a forma polar:
Passo 3
Multiplicando esses dois fasores na forma polar teremos:
Passo 4
Nossa expressão se tornou:
Para fazer a divisão, temos que transformar o divisor para a forma polar:
Passo 5
Resposta
Exercício Resolvido #10
Introdução a Análise de Circuitos - 12˚ ed – Capítulo 14 – Exercício 50
- Determine uma solução para e se:
- Determine se:
Passo 1
Vamos fazer a letra a, primeira coisa é transformar o fasor da forma polar para a forma retangular:
Como o ângulo era igual a zero, só temos a parcela real.
Passo 2
Vamos fazer as operações entre as formas retangulares:
Passo 3
Agora vamos igualar os dois lados da equação, lembrando da separação entre a parte real e a parte imaginária.
Parte real:
Parte imaginária:
Passo 4
Letra b:
Primeiro passo é transformar o fasor da forma retangular para a forma polar:
Passo 5
Vamos fazer as operações entre as formas polares:
Passo 6
Agora só falta igualar os dois lados:
Resposta
- e
Exercício Resolvido #11
Livro Sadiku, Problema 34
Qual é o valor de que fará que a resposta forçada,, na figura, seja zero?
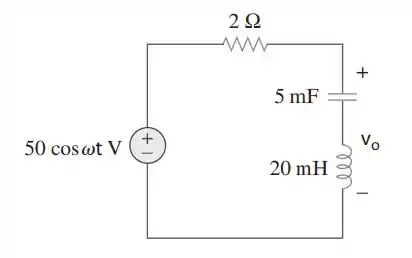
Passo 1
Vamos começar calculando nossas impedâncias:
Passo 2
Agora, basta igualarmos a equação de a zero:
Resposta
Exercício Resolvido #12
Livro Sadiku, Problema 9.16
Transforme as senoides a seguir em fasores:
(a)
(b)
(c)
Passo 1
- Essa aqui é bem simples! Basta colocar na forma polar:
- Pra resolver essa letra b, vamos precisar passar de seno para cosseno para colocarmos na forma fasorial polar:
Passo 2
Então, nomeando essa função como , vamos passá-la para cosseno diminuindo de seu ângulo.
Passo 2
(c) Para essa, vamos somar as duas partes, mas antes, precisamos passar a parte do seno para cosseno para podermos somar
Agora, vamos passar as duas partes para suas formas fasoriais polares
E para somá-los, o mais fácil é passá-los para a forma retangular:
Somando vamos ter e passando para a forma polar de novo usando as fórmulas:
e
Chegamos em
Resposta
(a)
(b)
(c)
Exercício Resolvido #13
Livro Sadiku, Problema 7
Se , demonstre que .
Passo 1
Meio complicado né? Mas vamos começar pensar na derivada…
Bom, se nós derivarmos essa função, temos:
Como
e como , então
Passo 2
Agora vamos começar com as manipulações matemáticas… tem que ter algumas sacadas, mas vamos aprender aqui que é bem fácil!
A gente vai querer integrar dos dois lados, então vamos fazer uma multiplicação cruzada entre o e o
(aqui usamos a exponencial para se livrar do )
Então,
Passo 3
Agora vamos igualar essa equação que achamos com a do enunciado…
Para achar o vamos usar usar a condição inicial para
Substituindo o na equação, temos:
E assim, tá provado!