Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Impedância Elétrica

Ver Todos os Exercícios

Teoria

A impedância é a soma vetorial da resistência e da reatância de um componente e seu módulo pode ser calculado usando a seguinte fórmula:

Onde é a tensão e é a corrente elétrica e a impedância é medida em ohms .

-Opa, mas essa não é a fórmula da resistência elétrica?!

Parece, não é? A ideia é até um pouco parecida mas impedância e resistência são coisas diferentes! A impedância é composta por uma parte real, que é a resistência e uma parte imaginária, que é a reatância.

Pra cada tipo de circuito a gente calcula a impedância de uma forma diferente, a gente vai ver isso já já, mas antes… precisamos relembrar algumas definições importantes:

  • Resistência é a dificuldade que um condutor oferece à corrente elétrica, a resistência é a parte real da impedância;

  • Reatância é a redução da passagem de corrente causada por campos elétricos e magnéticos que se opõem às mudanças da corrente elétrica ou tensão. A reatância representa a parte imaginária da impedância.

Agora, se liga nesse vídeo supercompleto sobre Impedância Elétrica 👇

Ou continua comigo no textinho, vamos ver como calcular a impedância em cada tipo de circuito! 👇 😉

Circuito Puramente Resistivo

Em um circuito puramente resistivo a tensão e corrente estão em fase, ou seja, apresentam o mesmo ângulo de fase.

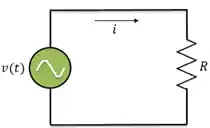
Circuito puramente resistivo
Circuito puramente resistivo

Podemos escrever:

Podemos então encontrar a impedância, fazendo:

Portanto, neste caso, a impedância só possui parte real e é simplesmente a resistência do circuito.

Circuito Puramente Capacitivo

Agora, vamos fazer a mesma análise para um circuito puramente capacitivo.

Circuito puramente capacitivo.
Circuito puramente capacitivo.

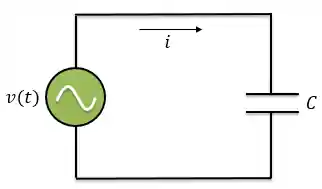
No primeiro tópico vimos que no caso puramente capacitivo a tensão e a corrente estão fora de fase por um ângulo de Mais precisamente, a corrente está adiantada em relação à tensão.

Pela lei de Ohm, dividindo a tensão fasorial pela corrente fasorial , encontramos a impedância :

Como podemos ver, é um número complexo e passando para forma retangular temos:

Portanto, neste caso, a impedância só possui parte imaginária e é negativa.

Circuito Puramente Indutivo

Agora, vamos ver como funciona no indutor.

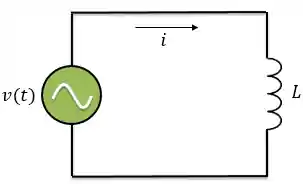
Circuito puramente indutivo.
Circuito puramente indutivo.

Nesse caso a corrente é atrasada em relação à tensão por um ângulo de .

Pela lei de Ohm, dividindo a tensão fasorial pela corrente fasorial , encontramos a impedância . Portanto, para esse caso, temos:

Passando a impedância para forma retangular temos:

Agora que você já esta sabendo tudo sobre impedância elétrica, vamos praticar com exercícios?

Circuito Puramente Resistivo

Circuito Puramente Capacitivo

Circuito Puramente Indutivo

Exercícios Resolvidos

Exercício Resolvido #1

Livro Sadiku, p.362, Problema 9.35

Determine a corrente i   no circuito abaixo quando v s t = 50 cos ⁡ 200 t   V .

Passo 1

Para determinar a corrente nesse exercício, vamos trabalhar com fasores e teremos que encontrar a impedância do circuito, porque a corrente será:

I = V Z

Como temos um capacitor e um indutor, calcularemos a reatância capacitiva e reatância indutiva, já que como esses elementos estão em série a impedância será:

Z = R - j X C + j X L

Passo 2

Lembrando que através da equação fornecida da tensão, podemos encontrar a frequência angular ω :

v s t = 50 cos ⁡ 200 t   V

Logo, ω = 200   r a d / s .

Calculando a reatância capacitiva, fazemos:

X C = 1 ω C = 1 200 × 5 × 10 - 3 = 1 Ω            

Calculando a reatância indutiva, fazemos:

X L = ω L = 200 × 20 × 10 - 3 = 4 Ω

Passo 3

Agora já podemos calcular a impedância:

Z = R - j X C + j X L

Z = 10 - j 1 + j 4

Z = 10 + j 3  

Passo 4

Como vamos precisar dividir a tensão pela impedância para calcular a corrente, temos que passar ambas as grandezas para a forma polar.

Primeiro a tensão. Como ela já está na forma de cosseno, a transformação é direta:

v s t = 50 cos ⁡ 200 t   → V = 50 ∠ 0 °

Agora a impedância. Você lembra como fazemos para passar para a forma polar? Primeiro a gente tem que achar o módulo:

Z =   10 2 + 3 2   = 10,44

O ângulo será:

tan - 1 ⁡ 3 10 = 16,7 °

Portanto, a impedância na forma polar é:

Z = 10,44 ∠ 16,7 °   Ω

Passo 5

Finalmente podemos calcular a corrente:

I = 50 ∠ 0 ° 10,44 ∠ 16,7 °

I = 4,79 ∠ - 16,7 °   A  

Agora é só voltar para o domínio do tempo:

i = 4,79 cos ⁡ 200 t - 16,7 °   A

Resposta

i = 4,79 cos ⁡ 200 t - 16,7 °   A

Exercício Resolvido #2

Livro Sadiku, p.363, Problema 9.37

Determine a admitância Y para o circuito abaixo:

Passo 1

A admitância do circuito será dada por:

Y = 1 Z e q

Temos três impedâncias no circuito acima:

Z 1 = 4 Ω

Z 2 = j 8 Ω

Z 3 = - j 10 Ω

Passo 2

Como as impedâncias estão em paralelo, a impedância equivalente será dada por:

1 Z e q = 1 Z 1 + 1 Z 2 + 1 Z 3

Passo 3

Como será necessário fazer divisão, vamos passar as impedâncias para a forma polar:

Z 1 = 4 →   Z 1 = 4 ∠ 0 °

Z 2 = j 8 →   Z 2 = 8 ∠ 90 °

Z 3 = - j 10   →   Z 3 = 10 ∠ - 90 °

Passo 4

Calculando a impedância equivalente:

1 Z e q = 1 Z 1 + 1 Z 2 + 1 Z 3

1 Z e q = 1 4 ∠ 0 ° + 1 8 ∠ 90 ° + 1 10 ∠ - 90 °

1 Z e q = 0,25 ∠ 0 ° + 0,125 ∠ - 90 ° + 0,1 ∠ 90 °

Passo 5

Agora, como vamos ter que somar, teremos que passar cada parcela da impedância equivalente para a forma retangular. Lembrando que:

j = 1 ∠ 90 °

- j = 1 ∠ - 90 °

Logo:

1 Z e q = 0,25 - j 0,125 + j 0,1

1 Z e q = 0,25 - j 0,025

Passo 6

A admitância é, então:

Y = 1 Z e q = 0,25 - j 0,025   S

Resposta

Y = 0,25 - j 0,025     S

Exercício Resolvido #3

Livro Sadiku, p.364, Problema 9.56

Com ω = 377   r a d / s , determine a impedância de entrada do circuito abaixo:

Passo 1

A impedância de entrada do circuito será:

Z e n t r a d a = R - j X C + Z e q 1

Onde Z e q 1 é a impedância equivalente entre o paralelo da reatância indutiva com resistência de 40   Ω .

Vamos primeiro calcular as reatâncias do circuito.

j X L = j ω L = j 377 × 60 × 10 - 3 = j 22,62 Ω  

- j X C = - j 1 ω C = - j 1 377 × 50 × 10 - 6 = - j 53,05 Ω

Passo 2

Agora precisaremos calcular o paralelo entre a reatância indutiva e a resistência:

Z e q 1 = j X L × R j X L + R

Passando a reatância para a forma polar, teremos que:

j X L = 22,62 ∠ 90 °

Então:

Z e q 1 = 22,62 ∠ 90 ° × 40 j 22,62 + 40

Z e q 1 = 904,8 ∠ 90 ° 40 + j 22,62

Passando o denominador para a forma polar:

40 2 + 22,62 2 = 45,95

tan - 1 ⁡ 22,62 40 = 29,49 °

Logo:

Z e q 1 = 904,8 ∠ 90 ° 45,95 ∠ 29,49 °

Z e q 1 = 19,69 ∠ 60,51 °

Passo 3

Passando a impedância equivalente 1 para a forma retangular:

Z e q 1 = 19,69 × cos ⁡ 60,51 ° + j 19,69 × s e n 60,51 °

Z e q 1 = 9,69 + j 17,14

Passo 4

Já temos todos os dados para calcular a impedância de entrada:

Z e n t r a d a = R - j X C + Z e q 1

Z e n t r a d a = 12 - j 53,05 + 9,69 + j 17,14

Z e n t r a d a = 21,69 - j 35,91   Ω

Resposta

Z e n t r a d a = 21,69 - j 35,91   Ω

Exercício Resolvido #4

Livro Sadiku, p.363, Problema 9.39

Para o circuito abaixo determine Z e q e use esta para determinar a corrente I . Considere ω = 10   r a d / s .

Passo 1

Como existe uma reatância capacitiva em série com uma reatância indutiva, o equivalente será:

Z e q 1 = j 25 - j 14

Z e q 1 = j 11

Passo 2

Agora teremos que calcular a impedância equivalente referente entre o paralelo da resistência de 16   Ω e Z e q 1 .

Z e q 2 = j 11 × 16 j 11 + 16

Z e q 2 = j 176 16 + j 11

Passo 3

Como faremos uma divisão, é necessário passar o numerador e o denominador para a forma polar:

j 176   → 176 ∠ 90 °

Para o denominador, será necessário calcular o módulo e o ângulo da forma polar:

16 2 + 11 2 = 19,41

tan - 1 ⁡ 11 16 = 34,51 °

Logo:

16 + j 11   → 19,41 ∠ 34,51 °  

Passo 4

Agora podemos calcular a impedância equivalente 2:

Z e q 2 = 176 ∠ 90 ° 19,41 ∠ 34,51 °

Z e q 2 = 9,07 ∠ 55,49 °   Ω  

Passando para a forma retangular:

Z e q 2 = 9,07 × cos ⁡ 55,49 ° + j 9,07 × s e n 55,49 °  

Z e q 2 = 5,14 + j 7,47   Ω

Passo 5

A impedância equivalente total será:

Z e q = 4 + j 20 + Z e q 2

Z e q = 4 + j 20 + 5,14 + j 7,47

Z e q = 9,14 + j 27,47       Ω

Passando para a forma polar:

9,14 2 + 27,47 2 = 28,95

tan - 1 ⁡ 27,47 9,14 = 71,6 °

Logo:

Z e q = 28,95 ∠ 71,6 ° Ω

Passo 6

Por fim, a corrente será:

I = V Z e q

I = 12 ∠ 0 ° 28,95 ∠ 71,6 °

I = 0,4145 ∠ - 71,6 °   A

Resposta

I = 0,4145 ∠ - 71,6 °   A

Exercício Resolvido #5

Livro Sadiku, p.364, Problema 9.50

Determine v x no circuito abaixo. Considere i s = 5 cos ⁡ 100 t + 40 °   A .

Passo 1

Nosso primeiro passo é passar o circuito para o domínio da frequência para podermos trabalhar com fasores.

Primeiro a corrente. Como ela já está na forma de cosseno, a transformação é direta:

i s t = 5 cos ⁡ ( 1 00 t + 40 ° )   → I s = 5 ∠ 4 0 °

Calculando as reatâncias do circuito.

j X L = j ω L = j 100 × 0,1 = j 10   Ω  

- j X C = - j 1 ω C = - j 1 100 × 1 × 10 - 3 = - j 10   Ω

Passo 2

Logo, podemos estudar o circuito da seguinte forma:

Z 1 = - j X C = - j 10

Z 2 = R + j X L = 20 + j 10

Passo 3

Lembrando que tudo o que vimos para resistores é válido para impedâncias, já que também é válida as leis de Kirchhoff quando utilizamos fasores. Aplicando divisor de corrente, temos:

I 2 = I S × Z 1 Z 1 + Z 2

I 2 = 5 ∠ 40 ° × 10 ∠ - 90 ° - j 10 + 20 + j 10

I 2 = 5 ∠ 40 ° × 10 ∠ - 90 ° 20

I 2 = 2,5 ∠ - 50 °   A

Passo 4

Como I 2 passa pelo resistor de 20   Ω , aplicando a lei de Ohm, temos:

V x = 20 I 2 = 20 × 2,5 ∠ - 50 ° = 50 ∠ - 50 °   V  

Agora é só voltar para o domínio do tempo:

v x = 50 cos ⁡ 100 t - 50 °   V

Resposta

v x = 50 cos ⁡ 100 t - 50 °   V

Exercício Resolvido #6

Livro Sadiku, p.364, Problema 9.51

Se a tensão v 0 no resistor de 2   Ω no circuito abaixo for 10 cos ⁡ 2 t   V , obtenha i s .

Passo 1

Nosso primeiro passo é passar o circuito para o domínio da frequência para podermos trabalhar com fasores.

Primeiro a tensão v 0 . Como ela já está na forma de cosseno, a transformação é direta:

v 0 t = 10 cos ⁡ 2 t   → V 0 = 10 ∠ 0 °

Calculando as reatâncias do circuito.

j X L = j ω L = j 2 × 0,5 = j   Ω  

- j X C = - j 1 ω C = - j 1 2 × 0,1 = - j 5   Ω

Passo 2

Logo, podemos estudar o circuito da seguinte forma:

Z 1 = 1   Ω

Z 2 = R 2 Ω + j X L - j X C = 2 + j - j 5 = 2 - j 4

Passo 3

Aplicando divisor de corrente, temos:

I 2 = I S × Z 1 Z 1 + Z 2

I 2 = I S × 1 1 + 2 - j 4

I 2 = I S × 1 3 - j 4

Como faremos uma divisão, é necessário passar o denominador para a forma polar. Calculando o módulo e o ângulo da forma polar:

3 2 + 4 2 = 5

tan - 1 - ⁡ 4 3 = - 53,13 °

Logo:

3 - j 4   → 5 ∠ - 53,13 °  

Substituindo, temos:

I 2 = I S × 1 5 ∠ - 53,13 °

I S = I 2 × 5 ∠ - 53,13 °  

Passo 4

Estamos quase lá! Para encontrarmos I S só falta calcular o valor de I 2 . Se repararmos, a corrente I 2 passa pela impedância Z 2 e como esta impedância contém a resistência de 2   Ω , essa corrente também passa por este resistor. Logo, aplicando a lei de Ohm:

I 2 = V 0 R 2 Ω = 10 ∠ 0 ° 2 = 5 ∠ 0 °   A

Passo 5

Agora é só substituir:

I S = I 2 × 5 ∠ - 53,13 °  

I S = 5 ∠ 0 ° × 5 ∠ - 53,13 ° = 25 ∠ - 53,13 °   A  

Voltando para o domínio do tempo:

i s t = 25 cos ⁡ 2 t - 53,13 °   A

Resposta

i s t = 25 cos ⁡ 2 t - 53,13 °   A

Exercício Resolvido #7

Livro Sadiku, p.364, Problema 9.52

Se V 0 = 8 ∠ 30 °   V no circuito baixo, determine I s .

Passo 1

Bom, ele deu pra gente a tensão em cima de uma impedância né? Então é tranquilo achar a corrente nela!

I 0 = V 0 j 5 = 8 ∠ 30 ° 5 ∠ 90 ° = 1,6 ∠ - 60 °   A

Como a resistência de 5   Ω está em paralelo a tensão nela também vai ser V 0 !

Então a corrente por ela vai ser dada por

I 1 = V 0 5 = 8 ∠ 30 ° 5 ∠ 0 ° = 1,6 ∠ 30 °   A

Por enquanto temos isso:

Passo 2

Beleza, repara que I 2 = I 0 + I 1 ! Então,

I 2 = 1,6 ∠ - 60 ° + 1,6 ∠ 30 °  

I 2 = 0,8 - j 0,8 3 + 0,8 3 + j 0,8

I 2 = 0,8 1 + 3 + j 0,8 1 - 3

I 2 = 1,6 2 ∠ - 15 °

Conhecendo a corrente I 2 , podemos determinar a tensão no elemento - j 5   Ω :

V 2 = 1,6 2 ∠ - 15 ° ⋅ 5 ∠ - 90 ° = 8 2 ∠ - 105 °   V

Passo 3

Show de bola, a tensão em cima da resistência de 10   Ω vai ser então:

V 3 = V 2 + V 0 = 8 2 ∠ - 105 ° + 8 ∠ 30 °

V 3 = 8 ∠ - 60 °

Com isso podemos achar a corrente I 3 da figura abaixo!

I 3 = V 3 10 = 0,8 ∠ - 60 °

Passo 4

Agora pra acharmos I S é só somar I 2 e I 3 !

I S = 1,6 2 ∠ - 15 ° + 0,8 ∠ - 60 °

I S = 2,88 ∠ - 26,31 °

Resposta

I S = 2,88 ∠ - 26,31 °   A

Exercício Resolvido #8

Livro Sadiku, Problema 47

No circuito da figura, determine o valor de i s ( t ) .

Passo 1

Vamos calcular nossas impedâncias sabendo que ω = 2000 (basta olhar para a tensão)

Z 1 = j × 2000 × 2 × 10 - 3 + 20

Z 1 = 4 j + 20

Z 2 = ( 20 + 4 j ) 1 j × 2000 × 50 × 10 - 6 20 + 4 j + 1 j × 2000 × 50 × 10 - 6

Z 2 = ( 20 + 4 j ) ( - j 10 ) 20 + 4 j - j 10

Z 2 = 40 - 200 j 20 - 6 j × ( 20 + 6 j ) 20 + 6 j

Z 2 = ( 800   + 1200 ) + j ( 240 - 4000 ) 436

Z 2 = 4.587 - j 8.623

Passo 2

Agora, vamos calcular a impedância equivalente do circuito para poder calcular a corrente.

Z e q = 2 + 4.587 - j 8.623

Z e q = 6.587 - j 8.623

Então, a corrente i s ( t ) será:

i s ( t ) = V Z e q = 5 ∠ 0 ° 10.85 ∠ - 52.624 °

i s ( t ) = 0.46 ∠ 52.624 °

Então, no domínio do tempo teremos:

i s ( t ) = 0.46 c o s ( 2000 t + 52.624 ° )

Resposta

i s ( t ) = 0.46 c o s ( 2000 t + 52.624 ° )

Exercício Resolvido #9

Livro Sadiku, Problema 41

Determine v ( t ) no circuito RLC da figura

Passo 1

Vamos passar logo a nossa fonte para a forma fasorial polar

10 c o s t   =   10 ∠ 0 ° V

Agora vamos achar as reatâncias dos elementos passivos para ω = 1

X L = j ω L

X L = j Ω

X C = 1 j ω C

X C =   - j Ω

Passo 2

Agora vamos redesenhar o circuito mostrando as impedâncias no domínio complexo::

Passo 3

A partir dessa figura, vemos que temos 3 impedâncias, Z 1 , Z 2   e   Z 3

Para achar Z 1 , vamos somar:

Z 1 = ( 1 + j ) Ω

E, em seguida, vamos fazer o paralelo de Z 1 com Z 2 :

Z 1 / /   Z 2 =   ( 1 + j ) ( - j ) 1 + j - j

Z 1 / /   Z 2 = ( 1 - j ) Ω

Passo 4

Agora, observe que a tensão que passa pelas impedâncias em paralelo é a mesma que passa pelo capacitor, porque eles estão em paralelo. Então, podemos utilizar divisor de tensão para achar v ( t )

v ( t ) = ( 10 ∠ 0 ° ) Z 1 / /   Z 2 ( Z 1 / /   Z 2 ) + Z 3        

(aqui, note que usamos o valor da impedância Z 3 na forma polar)

v ( t ) = ( 10 ∠ 0 ° ) 1 - j 1 - j + 1        

v ( t ) = ( 10 ∠ 0 ° ) 1 - j 2 - j        

(passando para a forma polar…)

v ( t ) = ( 10 ∠ 0 ° ) 1.4142 ∠ - 45 ° 2.2361 ∠ - 26.57 °        

v ( t ) = 6.32 ∠ - 18.43 ° V

Passando para o domínio do tempo, teremos:

v ( t ) =   6.32 c o s ( t - 18.43 ° ) V

Resposta

v ( t ) =   6.32 c o s ( t - 18.43 ° ) V

Exercício Resolvido #10

Livro Sadiku, Problema 45

Determine a corrente I o no circuito da figura

Passo 1

Vamos primeiro redesenhar o circuito mostrando as correntes dos ramos

Passo 2

Vamos começar achando a impedância equivalente do paralelo de - j 2 Ω com 2 Ω

Z e q =   2 / / - j 2

Z e q =   ( 2 ) ( - j 2 ) 2 - j 2

Z e q =   ( - j 2 ) 1 - j 1

Z e q = = j 2 ( 0.5 + j 0.5 )

Z e q = = 1 - j 1

Passo 3

Agora vamos redesenhar nosso circuito com a impedância equivalente que achamos

Passo 4

Com essa figura, podemos encontrar a corrente I 2 utilizando divisor de corrente:

I 2 = ( I 1 ) - j 2 - j 2 + j 4 + 1 - j 1        

I 2 = ( 5 ∠ 0 ° ) - j 2 - j 2 + j 4 + 1 - j 1        

I 2 = ( 5 ∠ 0 ° ) - j 2 1 + j 1        

I 2 = ( 5 ∠ 0 ° ) 2 ∠ 90 ° 1.414 ∠ 45 °        

I 2 = 7.072 ∠ - 135 ° A

Passo 5

Mas ainda não é isso que queremos. Nós queremos o I o

Analisando essa figura novamente

Podemos perceber que aqui, vamos aplicar divisor de corrente novamente para obter I o .

I o = ( I 2 ) - j 2 - j 2 + 2        

I o = ( 7.072 ∠ - 135 ° ) - j 2 - j 2 + 2        

(Substituímos o valor de I 2 que achamos no passo 4 e em seguida simplificamos a parte entre colchetes)

I o = ( 7.072 ∠ - 135 ° ) - j 1 - j 1 + 1        

I o = ( 7.072 ∠ - 135 ° ) 1 ∠ - 90 ° 1.414 ∠ 45 °        

I o =   5 A

Resposta

I o =   5 A

Exercícios de Livros Relacionados

Obtenha a impedância equivalente para o circuito da Figura 9.78.
a Calcule o deslocamento de fase do circuito da Figura 9.82. b Informe se o deslocamento de fase está avançado ou atrasado (saída em relação à entrada). c Determine a magnitude da saída quando a entra
Uma ponte de capacitância está equilibrada quando R 1 = 1 00Ω ,R 2 = 2 k ΩeC s = 40μ F . Qual o valor de C x , a capacitância do capacitor em teste?
55- Determine Z no circuito da Figura 9.62 dado que V_o = 4 /_ 0 ° V
O circuito da Figura 9.87 faz parte do esquema que descreve um sensor eletrônico industrial. Qual é a impedância total do circuito em 2k H z ?