Introdução à Circuitos CA
Produzido por Alexandre NunesTeoria
Funções Senoidais
Agora, nosso estudo é de circuitos alimentados por fontes de tensão ou corrente alternadas. Ou seja, fontes em que a tensão ou corrente variam com o tempo. Mais especificamente, estamos interessados em fontes que possuam sinais senoidais.
Por exemplo, no circuito abaixo vamos considerar que a fonte de tensão é
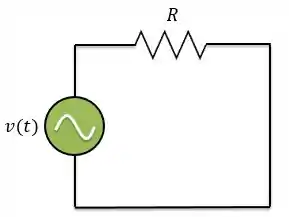
Onde,
é a amplitude da senóide;
é a frequência angular e tem a seguinte relação com a frequência da senóide:
é a fase.
Portanto, ela tem a seguinte forma de onda:
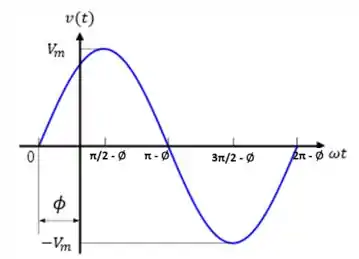
Como a função senoidal é periódica, ela apresenta um período que é o tempo necessário para se completar um ciclo. Portanto,
Então, para ver se estamos sabendo, vamos determinar a amplitude, fase, frequência e período da senóide abaixo:
Comparando com a expressão genérica que vimos
Temos,
A amplitude é ;
A fase é ;
A frequência angular é ;
A frequência é
O período é
Agora, vamos ver como cada elemento do circuito se comporta quando são alimentandos por fontes senoidas.
Circuito Puramente Resistivo
No circuito abaixo estamos aplicando no resistor uma fonte de tensão alternada da seguinte forma
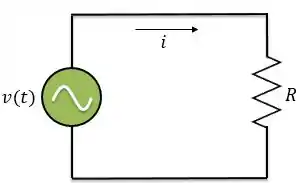
Aplicando a lei de Ohm encontraremos a corrente que circula pelo resistor,
Logo,
Sendo, a amplitude da corrente, temos
Neste circuito, observamos que tensão e corrente variam da mesma forma no tempo e não existe diferença de fase entre ambas. Ou seja, não há defasagem entre elas, já que apresentam a mesma fase .
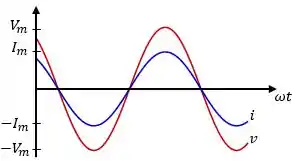
Em circuitos CA, é apresentado um novo termo: a impedância .

Ela é medida em ohms e, em módulo, é dada pela razão entre os valores de amplitude da tensão e da corrente .
Portanto, neste caso, a impedância é simplesmente a resistência do circuito.
Circuito Puramente Capacitivo
Agora, vamos aplicar no capacitor a mesma tensão
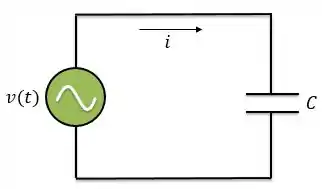
Sabemos que a relação de corrente no capacitor é
Logo, para encontrarmos a expressão para a corrente precisamos derivar a tensão .
Sendo, a amplitude da corrente, temos
Relembrando as identidades trigonométricas, temos que
Logo, a expressão da corrente é
Neste caso, a tensão e a corrente variam no tempo, mas estão fora de fase por um ângulo de .
Então, no circuito puramente capacitivo a corrente é adiantada em relação à tensão. Ou seja, o ponto de partida de ocorre antes no tempo do que o ponto de partida de , e o pico de máxima corrente ocorre antes da máxima tensão.
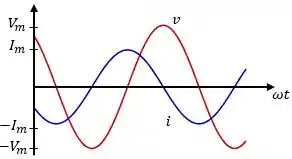
Esse adiantamento pode ser explicado pelo que estudamos sobre capacitor até aqui. Assim que o capacitor descarregado é ligado no circuito a corrente é máxima e a tensão é mínima, pois o capacitor está descarregado e a tensão em seus terminais não varia instantaneamente.
À medida que o tempo passa o capacitor vai se carregando e, consequentemente, a corrente vai diminuindo e a tensão aumentando. Até que o capacitor esteja completamente carregado, onde a corrente é zero e a tensão é máxima.
Vimos que o módulo da impedância é dada pela razão entre os valores de amplitude da tensão e da corrente . No caso de capacitores a impedância tem um nome específico. Ela é chamada de reatância capacitiva .
Como,
Temos que o módulo da reatância capacitiva é
Então, vamos supor que temos um circuito puramente capacitivo, com um capacitor de e queremos calcular a reatância capacitiva. Sabendo que a frequência do circuito é .
Como,
Substituindo,
Circuito Puramente Indutivo
Agora, vamos aplicar no indutor a mesma tensão
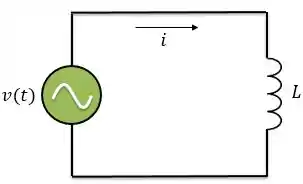
Sabemos que a corrente que circula pelo indutor pode ser calculada da seguinte forma:
Logo, para encontrarmos a expressão para a corrente, precisamos integrar a tensão .
Sendo a amplitude da corrente
Temos,
Relembrando as identidades trigonométricas, temos que
Logo, a expressão da corrente é
Então, no indutor, assim como nos casos anteriores, a tensão e a corrente variam periodicamente no tempo. Mas, nesse caso a corrente é atrasada em relação à tensão por um ângulo de .
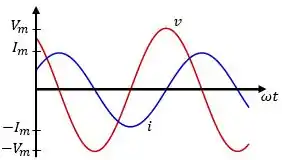
Isso pode ser explicado de maneira análoga ao que ocorre no capacitor. Como no indutor a corrente não varia instantaneamente, o pico de máxima tensão no indutor ocorre antes da máxima corrente e, portanto, a tensão está adiantada em relação à corrente.
Assim como no caso de capacitores, em indutores a impedância também tem um nome específico. Ela é chamada de reatância indutiva .
Como,
Temos que o módulo da reatância indutiva é
Agora é praticar! Vamos nessa!
Circuito Puramente Resistivo
Circuito Puramente Capacitivo
Circuito Puramente Indutivo
Exercícios Resolvidos
Exercício Resolvido #1
Livro Sadiku, p.360, Problema 9.1
Dada a tensão senoidal , determine:
a amplitude ;
o período ;
a frequência ;
em .
Passo 1
Basicamente, temos que comparar
com a expressão genérica
e aplicar fórmulas.
Passo 2
Comparando, vemos de cara que a amplitude é
Passo 3
Podemos encontrar o período pela relação abaixo:
Comparando as expressões vemos que
Portanto,
Passo 4
A frequência é o inverso do período. Logo,
Passo 5
Para terminar, precisamos calcular , para quando . Portanto,
Simplificando,
Precisamos ter cuidado agora! Não podemos somar os argumentos que estão dentro dos parênteses, pois estão em unidades diferentes. Um está em radiano e o outro em graus.
Então, precisamos converter um desses ângulos antes de calcular o cosseno.
Passando para graus:
Passo 6
\Substituindo,
Resposta
Exercício Resolvido #2
Livro Sadiku, p.361, Problema 9.3
Expresse as seguintes funções na forma de cosseno:
Passo 1
Para expressarmos as funções na forma de cosseno, precisamos relembrar de trigonometria e saber das seguintes relações:
É só lembrar que se o sinal que acompanha o seno for negativo, a gente soma no argumento do ângulo. Enquanto que se o sinal que acompanha o seno for positivo a gente subtrai .
Passo 2
Logo, aplicando a segunda relação em , temos:
Logo,
Passo 3
Para expressarmos em forma de cosseno, vamos utilizar a primeira relação. Então,
Passo 4
Para terminar, temos que expressar em forma de cosseno. Para isso, vamos utilizar a primeira relação:
Logo,
Resposta
Exercício Resolvido #3
Livro Sadiku, p.361, Problema 9.5
Dado e , determine o ângulo de fase entre as duas senoides e indique qual delas está atrasada em relação à outra.
Passo 1
Para a gente comparar e , precisamos que elas estejam expressas da mesma forma. Então, primeiramente, vamos expressar na forma de cosseno. Sabendo que:
Nós poderíamos passar também a tensão para a forma de seno, mas optamos por trabalhar com todas na forma de cosseno, pois é mais habitual.
Temos,
Como preferimos trabalhar com ângulos positivos, podemos somar a um ângulo negativo para obter sua forma positiva sem alterar a direção do mesmo.
Logo também podemos escrever assim:
Passo 2
Para ajudar na visualização, vamos expressar com ângulo de fase positivo. Para isso, somamos como fizemos anteriormente.
Passo 3
Agora, para determinar o ângulo de fase entre as tensões, vamos olhar o diagrama fasorial das tensões:
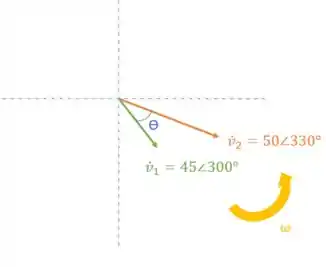
Percebemos que basta subtrair as fases:
Podemos observar que como a fase de é menor do que a fase de , dizemos que está atrasada em relação a . Na dúvida é só olhar no diagrama que o fasor de vai passar pela referência depois do do fasor !
Resposta
O ângulo de fase entre as tensões é e está atrasada em relação a .
Exercício Resolvido #4
Elaboração própria
Calcular a reatância de um capacitor de nas frequências de e .
Passo 1
Sabemos que a reatância capacitiva tem a seguinte fórmula:
Ou seja, ela só depende da frequência e do valor da capacitância.
Passo 2
Sabemos que
Logo,
Passo 3
O enunciado nos disse que . Portando, quando a frequência é de , temos:
Passo 4
Agora, vamos calcular a reatância capacitiva na frequência de .
Resposta
Exercício Resolvido #5
Elaboração própria
Calcular a reatância de uma bobina sabendo que ela tem de indutância e está sendo ligada a uma tensão de , .
Passo 1
Sabemos que a reatância indutiva tem a seguinte fórmula:
Ou seja, ela só depende da frequência e do valor da indutância.
Passo 2
O enunciado nos disse que e . Então, só precisamos calcular a frequência angular .
Como,
Logo,
Passo 3
Portando, substituindo na fórmula, temos:
Resposta
Exercício Resolvido #6
Elaboração própria
Em que frequência um capacitor de apresenta uma reatância de ?
Passo 1
Vimos na teoria que a reatância capacitiva tem a seguinte fórmula:
Passo 2
O enunciado nos disse que e . Logo, isolando a frequência angular:
Portanto,
Passo 3
Como a frequência tem a seguinte relação com a frequência angular,
Temos,
Logo,
Resposta
Exercício Resolvido #7
Elaboração própria
Em que frequência uma indutância de apresenta uma reatância de ?
Passo 1
Vimos na teoria que a reatância indutiva tem a seguinte fórmula:
Passo 2
O enunciado nos disse que e . Logo, isolando a frequência angular:
Portanto,
Passo 3
Como a frequência tem a seguinte relação com a frequência angular,
Temos,
Logo,
Resposta
Exercício Resolvido #8
Livro Sadiku, Problema 9.2
Uma fonte de corrente em um circuito linear tem .
(a) Qual a amplitude da corrente?
(b) Qual é a frequência angular?
(c) Determine a frequência da corrente?
(d) Calcule em
Passo 1
- Vamos analisar a forma geral para uma função no domínio do tempo:
- Analisando novamente a forma geral , vemos que:
Então a amplitude é .
Comparando com a função em questão, a amplitude será
Passo 2
Então:
Passo 2
(c) Para a frequência, temos que
Então, como ,
Passo 3
(d) Aqui, vamos substituir em.
Note que, passei de milissegundos para segundos pois temos que deixar no Sistema Internacional (SI).
Além disso, como estamos usando tudo em radianos (sabemos disso pois temos ), vamos passar para radianos também:
Substituindo tudo:
Resposta
(a)
(b)
(c)
(d)