Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Leis de Kirchhoff para Corrente Alternada

Ver Todos os Exercícios

Teoria

A gente viu que as Leis de Kirchhoff é válida para corrente alternada. Agora, vamos ver na prática a sua utilização para análise de circuitos CA. Para isso, vamos utilizar as técnicas de análise nodal e análise de malhas que serão executadas de maneira igual a quando estudamos circuitos CC.

Análise Nodal

Lembrando que a lei das correntes de Kirchhoff (LCK) é a base da análise nodal. Vamos fazer um exemplo passo-a-passo desse método em um circuito CA.

Então, vamos começar! No circuito abaixo, queremos determinar a corrente i utilizando análise nodal.

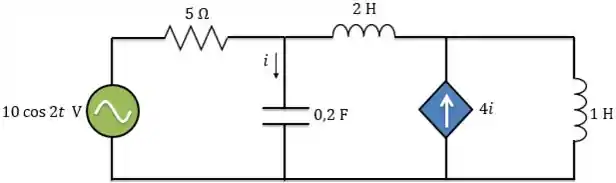
Passo 1:

De cara, temos que passar o circuito para o domínio da frequência, ou seja, para forma fasorial. Passando cada elemento, temos:

10 cos ⁡ 2 t       →       1 0 ∠ 0 °   ,         ω = 2   r a d / s

2   H       →       j ω L = j 4

1   H       →       j ω L = j 2

0,2   F       →   -   j 1 ω C   = - j 2,5

Logo, o circuito no domínio da frequência é:

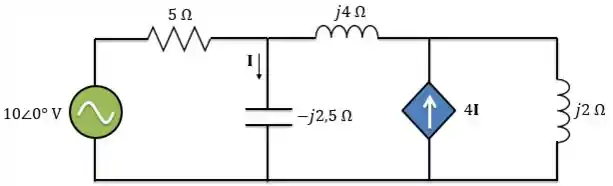
Passo 2:

Agora, vamos preparar o circuito para utilizar a análise nodal:

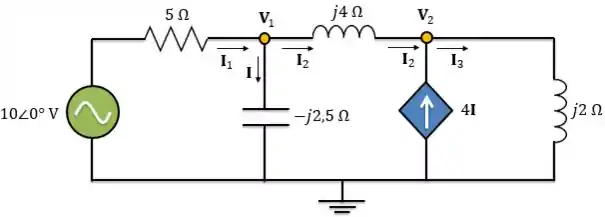
Aplicando a LCK ao nó 1:

I 1 = I + I 2

Como,

I 1 = 10 ∠ 0 ° - V 1 5   ;

I = V 1 - j 2,5   ;

I 2 = V 1 - V 2 j 4   ;

Substituindo,

10 ∠ 0 ° - V 1 5 = V 1 - j 2,5 + V 1 - V 2 j 4

Lembrando que

1 j = - j

Temos:

2 - 0,2 V 1 = j 0,4 V 1 - j 0,25 V 1 + j 0,25 V 2

0,2 + j 0,15 V 1 + j 0,25 V 2 = 2

Agora, aplicando a LCK ao nó 2:

I 2 + 4 I = I 3

Como,

I 3 = V 2 j 2

Logo,

V 1 - V 2 j 4 + 4 V 1 - j 2,5 = V 2 j 2

Simplificando a equação,

- j 0,25 V 1 + j 0,25 V 2 + j 1,6 V 1 = - j 0,5 V 2

j 1,35 V 1 + 0,75 V 2 = 0

1,35 V 1 + 0,75 V 2 = 0

Chegamos a um sistema:

0,2 + j 0,15 V 1 + j 0,25 V 2 = 2 1,35 V 1 + 0,75 V 2 = 0

Isolando V 2 na segunda equação e substituindo na primeira, temos:

0,2 + j 0,15 V 1 + j 0,25 - 1,8 V 1 = 2

0,2 + j 0,15 V 1 - j 0,45 V 1 = 2

0,2 - j 0,3 V 1 = 2

Passando para fórmula polar:

0,2 - j 0,3       →       0,36 ∠ - 56,31 °

Portanto,

V 1 = 2 0,36 ∠ - 56,31 °

V 1 = 5,55 ∠ 56,31 °   V

Logo, a corrente será:

I = V 1 - j 2,5

I = 5,55 ∠ 56,31 °   2,5 ∠ - 90 ° = 2,22 ∠ 146,31 °   A

Passo 3:

Agora é só voltar para o domínio do tempo:

i t = 2,22 cos ⁡ 2 t + 146,31 °   A

Análise de Malha

Assim como a LCK é a base da análise nodal, a lei das tensões de Kirchhoff (LTK) é a base para a análise de malha. Então, no circuito abaixo, vamos determinar a corrente i x utilizando análise de malha.

Passo 1:

Primeiro, temos que passar o circuito para o domínio da frequência. Passando cada elemento, temos:

5 cos ⁡ 4 t       →       5 ∠ 0 °   ,         ω = 4   r a d / s

20 cos ⁡ ( 4 t + 90 ° )       →       20 ∠ 90 °   ,         ω = 4   r a d / s

2   H       →       j ω L = j 8

0,5   F       →   -   j 1 ω C   = - j 0,5

0,25   F       →   -   j 1 ω C   = - j 1

Logo, o circuito no domínio da frequência é:

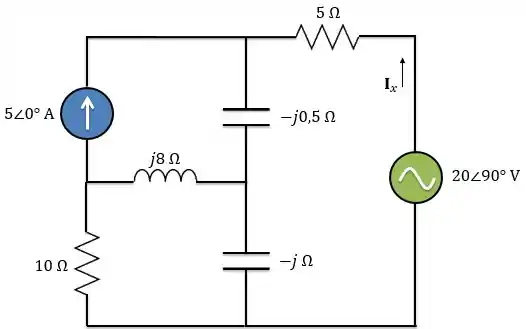
Passo 2:

Agora, vamos preparar o circuito para utilizar a análise de malha:

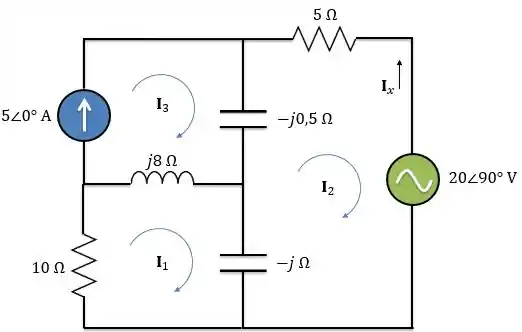
Aplicando a LTK na malha 1:

10 I 1 + j 8 I 1 - I 3 + - j I 1 - I 2 = 0

10 I 1 + j 8 I 1 - j 8 I 3 - j I 1 + j I 2 = 0

Se analisarmos a malha 3, vemos que

I 3 = 5

Substituindo e simplificando, temos:

10 + j 7 I 1 + j I 2 = j 40

Agora, aplicando LTK na malha 2:

- j I 2 - I 1 + - j 0,5 I 2 - I 3 + 5 I 2 + 20 ∠ 90 ° = 0

- j I 2 + j I 1 - j 0,5 I 2 + j 0,5 I 3 + 5 I 2 = - j 20

Como I 3 = 5 , temos:

j I 1 + 5 - j 1,5 I 2 = - j 20 - j 2,5

Chegamos a um sistema:

10 + j 7 I 1 + j I 2 = j 40 j I 1 + 5 - j 1,5 I 2 = - j 22,5

Isolando I 1 na primeira equação e substituindo na segunda, temos:

j j 40 - j I 2 10 + j 7 + 5 - j 1,5 I 2 = - j 22,5

Passando para forma polar:

1 ∠ 90 ° 40 ∠ 90 ° - I 2 ∠ 90 ° 12,2 ∠ 35 ° + 5,22 I 2 ∠ - 16,69 ° = 22,5 ∠ - 90 °

40 ∠ 180 �� 12,2 ∠ 35 ° - I 2 ∠ 180 ° 12,2 ∠ 35 ° + 5,22 I 2 ∠ - 16,69 ° = 22,5 ∠ - 90 °

3,28 ∠ 145 ° - 0,082 I 2 ∠ 145 ° + 5,22 I 2 ∠ - 16,69 ° = 22,5 ∠ - 90 °

I 2 5,22 ∠ - 16,69 ° - 0,082 ∠ 145 ° = 22,5 ∠ - 90 ° - ( 3,28 ∠ 145 ° )

Voltando para retangular:

I 2 5 - j 1,5 + 0,067 - j 0,047 = - j 22,5 + 2,68 - j 1,88

I 2 = 2,68 - j 24,38 5,067 - j 1,547  

Agora é passar para forma polar e efetuar a divisão:

I 2 = 24,53 ∠ - 83,72 ° 5,3 ∠ - 16,97 ° = 4,63 ∠ - 66,75 °   A

Como I x =   - I 2 , temos:

I x = -   4,63 ∠ - 66,75 ° = 4,63 ∠ 113,25 °   A

Passo 3:

Agora é só voltar para o domínio do tempo:

i x t = 4,63 cos ⁡ 4 t + 113,25 °   A

É isso! Missão cumprida!

Então, temos que seguir esses 3 passos para analisar o circuito em CA:

  1. Passar o circuito para o domínio da frequência;
  2. Resolver utilizando as técnicas que conhecemos (análise nodal, análise de malha, etc)
  3. Converter a resposta para o domínio do tempo.

Seguindo esses passos não tem erro! Separei exercícios para você fixar tudo isso. Agora é praticar.

Análise de Malha

Exercícios Resolvidos

Exercício Resolvido #1

Livro Sadiku, p.395, Problema 10.1

Determine i no circuito abaixo:

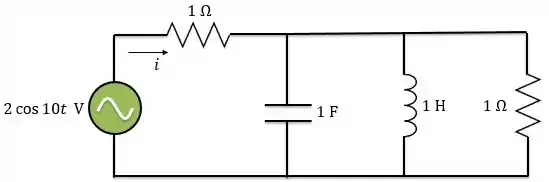
Passo 1

De cara, temos que passar o circuito para o domínio da frequência, ou seja, para forma fasorial. Passando cada elemento, temos:

2 cos ⁡ 10 t       →       2 ∠ 0 °   ,         ω = 10   r a d / s

1   H       →       j ω L = j 10

1   F       →   -   j 1 ω C   = - j 0,1

Logo, o circuito no domínio da frequência é:

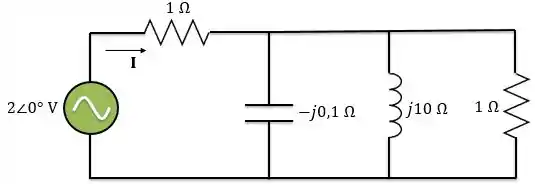
Passo 2

Agora, vamos preparar o circuito para utilizar a análise nodal:

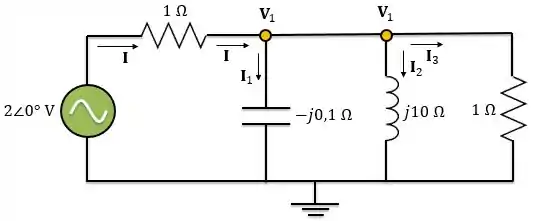
Aplicando a LCK ao nó:

I = I 1 + I 2 + I 3

Como,

I = 2 ∠ 0 ° - V 1 1   ;

I 1 = V 1 - j 0,1   ;

I 2 = V 1 j 10   ;

I 3 = V 1 1

Substituindo,

2 ∠ 0 ° - V 1 1 = V 1 - j 0,1 + V 1 j 10 + V 1 1

Lembrando que

1 j = - j

Temos:

2 - V 1 = j 10 V 1 - j 0,1 V 1 + V 1

2 V 1 + j 9,9 V 1 = 2

2 + j 9,9 V 1 = 2

V 1 = 2 2 + j 9,9

Passando para fórmula polar:

2 + j 9,9       →       r = 2 2 + 9,9 2 = 10,1   ;         ϕ = tan - 1 ⁡ 9,9 2 = 78,58 °       →     1 0 , 1 ∠ 78,58 °

Portanto,

V 1 = 2 10,1 ∠ 78,58 °

V 1 = 0,198 ∠ - 78,58 °   V

Passo 3

Como,

I = 2 ∠ 0 ° - V 1 1

Substituindo,

I = 2 ∠ 0 ° - 0,198 ∠ - 78,58 ° 1

Passando para forma retangular:

0,198 ∠ - 78,58 °       →       0,198 cos ⁡ - 78,58 ° + j 0,198 sen ⁡ - 78,58 ° = 0,039 - j 0,194

Logo,

I = 2 - 0,039 - j 0,194

I = 1,961 + j 0,194   A

Passando a corrente para forma polar:

1,961 + j 0,194       →       r = 1,961 2 + 0,194 2 = 1,97   ;       ϕ = tan - 1 ⁡ 0,194 1,961 = 5,65 °

Portanto,

I = 1,97 ∠ 5,65 °   A

Passo 4

Agora é só voltar para o domínio do tempo:

i t = 1,97 cos ⁡ 10 t + 5,65 °   A

Resposta

i t = 1,97 cos ⁡ 10 t + 5,65 °   A

Exercício Resolvido #2

Livro Sadiku, p.395, Problema 10.3

Determine v 0 no circuito abaixo:

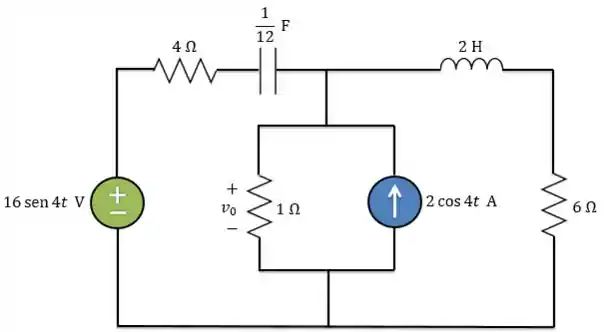
Passo 1

Primeiro, temos que passar o circuito para o domínio da frequência, ou seja, para forma fasorial. Como o a fonte de tensão está expressa em seno, antes de passar para forma fasorial precisamos escrever em termos de cosseno:

16 sen ⁡ 4 t = 16 cos ⁡ ( 4 t - 90 ° )

Passando cada elemento, temos:

16 cos ⁡ ( 4 t - 90 ° )       →       16 ∠ - 90 °   ,         ω = 4   r a d / s  

2 cos ⁡ 4 t       →       2 ∠ 0 °   ,         ω = 4   r a d / s

2   H       →       j ω L = j 8

1   F       →   -   j 1 ω C   = - j 3

Logo, redesenhando o circuito e passando para o domínio da frequência, temos:

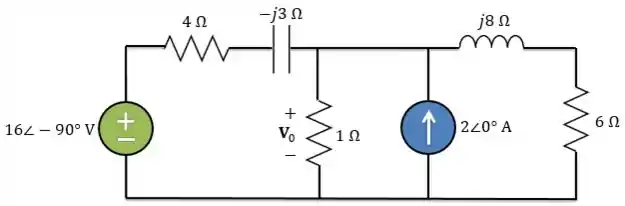
Passo 2

Agora, vamos preparar o circuito para utilizar a análise nodal:

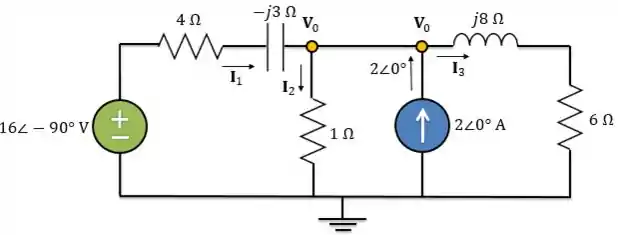Aplicando a LCK ao nó:

I 1 + 2 ∠ 0 ° = I 2 + I 3

Como,

I 1 = 16 ∠ - 90 ° - V 0 4 - j 3   ;

I 2 = V 0 1   ;

I 3 = V 0 6 + j 8

Substituindo,

16 ∠ - 90 ° - V 0 4 - j 3 + 2 ∠ 0 ° = V 0 1 + V 0 6 + j 8

16 ∠ - 90 ° 4 - j 3 + 2 ∠ 0 ° = V 0 1 + 1 6 + j 8 + 1 4 - j 3

Agora é só simplificar, para isso vamos precisar ficar passando os números complexos da forma polar para retangular e vice-versa.

16 ∠ - 90 ° 5 ∠ - 36,87 ° + 2 ∠ 0 ° = V 0 1 + 1 10 ∠ 53,13 ° + 1 5 ∠ - 36,87 °

3 , 2 ∠ - 53,13 ° + 2 ∠ 0 ° = V 0 1 + 0,1 ∠ - 53,13 ° + 0,2 ∠ 36,87 °

1,92 - j 2,56 + 2 = V 0 ( 1 + 0,06 - j 0,08 + 0,16 + j 0,12 )

V 0 = 3,92 - j 2,56 1,22 + j 0,04

V 0 = 4,68 ∠ - 33,15 ° 1,22 ∠ 1,88 °  

V 0 = 3,84 ∠ - 35,03 °     V

Passo 3

Agora é só voltar para o domínio do tempo:

v t = 3,84 cos ⁡ 4 t - 35,03 °   V

Resposta

v t = 3,84 cos ⁡ 4 t - 35,03 °   V

Exercício Resolvido #3

Livro Sadiku, p.395, Problema 10.7

Use a análise nodal para determinar V no circuito abaixo:

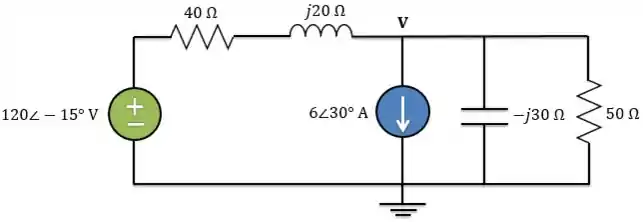
Passo 1

O circuito já está pronto para a gente trabalhar com fasores, pois já está no domínio da frequência. Além disso, precisamos determinar o fasor V . Logo, nosso resultado final não precisará ser escrito no domínio do tempo.

Passo 2

Agora, vamos preparar o circuito para utilizar a análise nodal:

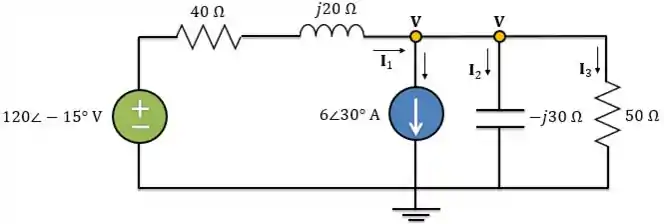
Aplicando a LCK ao nó:

I 1 = 6 ∠ 30 ° + I 2 + I 3

Como,

I 1 = ( 120 ∠ - 15 ° ) - V 40 + j 20   ;

I 2 = V - j 30   ;

I 3 = V 50

Substituindo,

( 120 ∠ - 15 ° ) - V 40 + j 20 = 6 ∠ 30 ° + V - j 30 + V 50

( 120 ∠ - 15 ° ) 40 + j 20 - 6 ∠ 30 ° = V 40 + j 20 + V - j 30 + V 50

( 120 ∠ - 15 ° ) 40 + j 20 - 6 ∠ 30 ° = V 1 40 + j 20 + 1 - j 30 + 1 50

Passo 3

Agora é só simplificar, para isso vamos precisar ficar passando os números complexos da forma polar para retangular e vice-versa.

120 ∠ - 15 ° 44,72 ∠ 26,56 ° - 6 ∠ 30 ° = V 1 44,72 ∠ 26,56 ° + 1 30 ∠ - 90 ° + 1 50

2,68 ∠ - 41,56 ° - 6 ∠ 30 ° = V 0,022 ∠ - 26,56 ° + 0,033 ∠ 90 ° + 0,02

2 - j 1,78 - ( 5,2 + j 3 ) = V 0,0197 - j 0,0098 + j 0,033 + 0,02

- ( 3,2 + j 4,78 ) = V ( 0,0397 + j 0,0232 )

V = - 3,2 + j 4,78 0,0397 + j 0,0232

V = - 3,2 + j 4,78 0,0397 + j 0,0232

V = - 5,75 ∠ 56,2 ° 0,046 ∠ 30,3 °

V = - 5,75 ∠ 56,2 ° 0,046 ∠ 30,3 °

V = - 125 ∠ 25,9 °     V

Passo 4

Agora, para terminar, precisamos deixar o fasor com módulo positivo. Para isso, basta somar ou subtrair 180 ° ao ângulo. Nesse caso, vamos subtrair:

V = 125 ∠ - 154,1 °     V

Resposta

V = 125 ∠ - 154 , 1 °     V

Exercício Resolvido #4

Livro Sadiku, p.395, Problema 10.6

Determine V x no circuito abaixo:

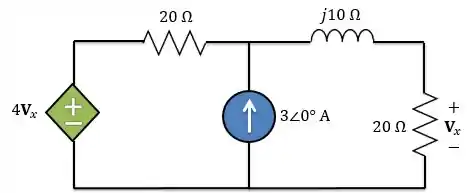
Passo 1

O circuito já está pronto para a gente trabalhar com fasores, pois já está no domínio da frequência. Além disso, precisamos determinar o fasor. Logo, nosso resultado final não precisará ser escrito no domínio do tempo.

Passo 2

Agora, vamos preparar o circuito para utilizar a análise nodal:

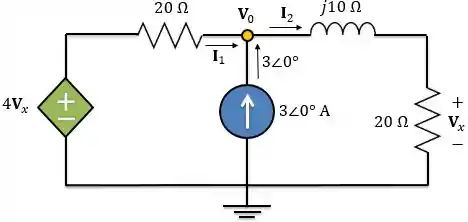
Aplicando a LCK ao nó:

I 1 + 3 ∠ 0 ° = I 2

Como,

I 1 = 4 V x - V 0 20   ;

I 2 = V 0 20 + j 10   ;

Substituindo,

4 V x - V 0 20 + 3 ∠ 0 ° = V 0 20 + j 10       i

Passo 3

Precisamos encontrar mais uma equação que relacione V x e V 0 para podemos encontrar o que queremos. Para isso, vamos utilizar divisor de tensão:

V x = 20 20 + j 10 V 0

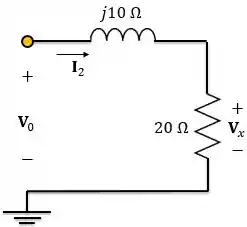
Logo,

V 0 = 20 + j 10 20 V x     ( i i )

Passo 4

Agora temos duas equações:

4 V x - V 0 20 + 3 ∠ 0 ° = V 0 20 + j 10       i

V 0 = 20 + j 10 20 V x     ( i i )

Substituindo i i em ( i ) :

4 V x 20 - 1 20 20 + j 10 20 V x + 3 = 1 20 + j 10 20 + j 10 20 V x

4 V x 20 - 20 + j 10 400 V x + 3 = V x 20

4 V x 20 - 20 + j 10 400 V x - V x 20 = - 3

V x 4 20 - 20 + j 10 400 - 1 20 = - 3

V x = - 3 0,15 - 0,056 ∠ 26,56 °

V x = - 3 0,15 - 0,05 + j 0,025

V x = - 3 0,1 - j 0,025

V x = - 3 0,103 ∠ - 14 °

V x = - 29,12 ∠ 14 °     V

Passo 5

Agora, para terminar, precisamos deixar o fasor com módulo positivo. Para isso, basta subtrair 180 ° ao ângulo:

V x = 29,12 ∠ - 166 °     V

Resposta

V x = 29,12 ∠ - 166 °     V

Exercício Resolvido #5

Livro Sadiku, p.397, Problema 10.25

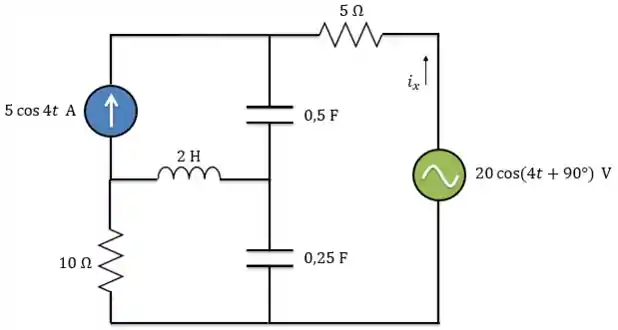
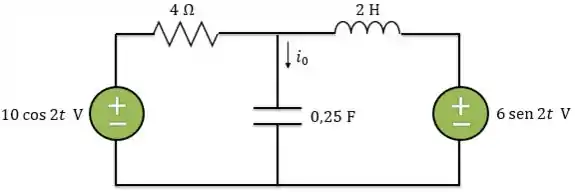
Determine i 0 no circuito abaixo usando a análise de malhas:

Passo 1

Primeiro, temos que passar o circuito para o domínio da frequência, ou seja, para forma fasorial. Como uma das fontes de tensão está expressa em seno, antes de passar para forma fasorial precisamos escrever em termos de cosseno:

6 sen ⁡ 2 t = 6 cos ⁡ ( 2 t - 90 ° )

Passando cada elemento, temos:

6 cos ⁡ ( 2 t - 90 ° )       →       6 ∠ - 90 °   ,         ω = 2   r a d / s  

10 cos ⁡ 2 t       →       10 ∠ 0 °   ,         ω = 2   r a d / s

2   H       →       j ω L = j 4

1   F       →   -   j 1 ω C   = - j 2

Logo, o circuito no domínio da frequência é:

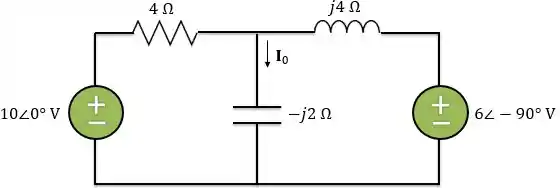
Passo 2

Agora, vamos preparar o circuito para utilizar a análise de malhas:

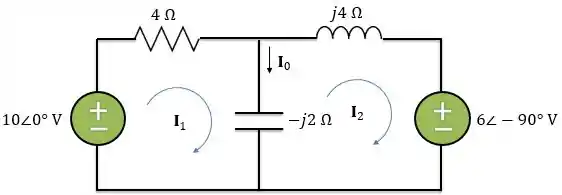
Aplicando a LTK na malha 1:

- 10 + 4 I 1 - j 2 I 1 - I 2 = 0

4 I 1 - j 2 I 1 + j 2 I 2 = 10

4 - j 2 I 1 + j 2 I 2 = 10

Agora, aplicando LTK na malha 2:

- j 6 - j 2 I 2 - I 1 + j 4 I 2 = 0

- j 2 I 2 + j 2 I 1 + j 4 I 2 = j 6

j 2 I 1 + j 2 I 2 = j 6

Dividindo toda equação por j 2 , temos:

I 1 + I 2 = 3

Passo 3

Chegamos a um sistema:

4 - j 2 I 1 + j 2 I 2 = 10 I 1 + I 2 = 3

Isolando I 2 na segunda equação e substituindo na primeira, temos:

4 - j 2 I 1 + j 2 ( 3 - I 1 ) = 10

4 - j 2 I 1 + j 6 - j 2 I 1 = 10

4 - j 4 I 1 = 10 - j 6

I 1 = 10 - j 6 4 - j 4

Passando para forma polar para efetuar a divisão:

I 1 = 11,66 ∠ - 30,96 ° 5,66 ∠ - 45 °

I 1 = 2,06 ∠ 14,04 °     A

Logo,

I 2 = 3 - I 1

I 2 = 3 - 2,06 ∠ 14,04 °

I 2 = 3 - ( 2 + j 0,5 )

I 2 = 1 - j 0,5     A

Analisando o circuito vemos que

I 0 = I 1 - I 2

Substituindo os valores que encontramos:

I 0 = 2 + j 0,5 - ( 1 - j 0,5 )

I 0 = 1 + j

I 0 = 1,414 ∠ 45 °     A

Passo 4

Agora é só voltar para o domínio do tempo. Lembrando que ω = 2   r a d / s , temos :

i t = 1,414 cos ⁡ 2 t + 45 °   A

Resposta

i t = 1,414 cos ⁡ 2 t + 45 °   A

Exercício Resolvido #6

Livro Sadiku, p.397, Problema 10.28

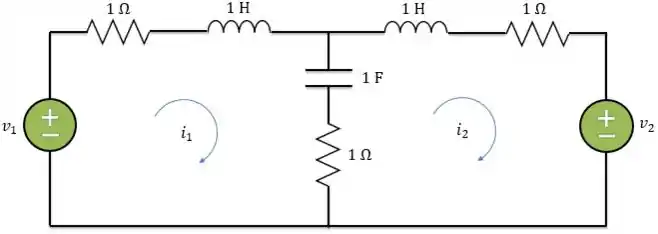
No circuito abaixo, determine as correntes de malha i 1 e i 2 . Seja v 1 = 10 cos ⁡ 4 t   V e v 2 = 20 cos ⁡ 4 t - 30 °   V .

Passo 1

Primeiro, temos que passar o circuito para o domínio da frequência. Passando cada elemento, temos:

10 cos ⁡ 4 t       →       10 ∠ 0 °   ,         ω = 4   r a d / s

20 cos ⁡ ( 4 t - 30 ° )       →       20 ∠ - 30 °   ,         ω = 4   r a d / s

1   H       →       j ω L = j 4

1   F       →   -   j 1 ω C   = - j 0,25

Logo, o circuito no domínio da frequência é:

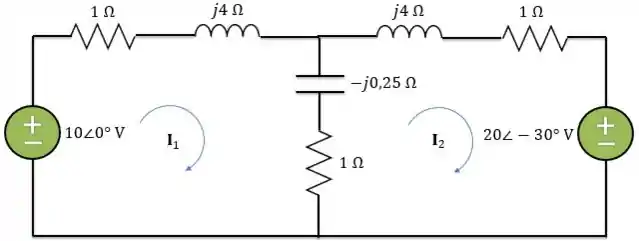
Passo 2

Aplicando a LTK na malha 1:

- 10 + I 1 + j 4 I 1 + 1 - j 0,25 I 1 - 1 - j 0,25 I 2 = 0

2 + j 3,75 I 1 - 1 - j 0,25 I 2 = 10

Aplicando a LTK na malha 2:

20 ∠ - 30 ° + 1 - j 0,25 I 2 - 1 - j 0,25 I 1 + 1 + j 4 I 2 = 0

- 1 - j 0,25 I 1 + 2 + j 3,75 I 2 = - 20 ∠ - 30 °

Passo 3

Então, precisamos resolver o sistema abaixo:

2 + j 3,75 I 1 - 1 - j 0,25 I 2 = 10 - 1 - j 0,25 I 1 + 2 + j 3,75 I 2 = - 20 ∠ - 30 °

Isolando I 1 na primeira equação, temos:

I 1 = 10 + 1 - j 0,25 I 2 2 + j 3,75  

I 1 = 10 + 1 - j 0,25 I 2 2 + j 3,75

I 1 = 10 2 + j 3,75 + 1 - j 0,25 2 + j 3,75 I 2

I 1 = 10 4,25 ∠ 61,93 ° + 1,03 ∠ - 14,04 ° 4,25 ∠ 61,93 ° I 2

I 1 = 2,35 ∠ - 61,93 ° + ( 0,242 ∠ - 75,97 ° ) I 2

Substituindo na segunda:

- 1 - j 0,25 ( 2,35 ∠ - 61,93 ° ) + 0,242 ∠ - 75,97 ° I 2 + 2 + j 3,75 I 2 = - 20 ∠ - 30 °

( - 1,03 ∠ - 14,04 ° ) ( 2,35 ∠ - 61,93 ° ) + 0,242 ∠ - 75,97 ° I 2 + 2 + j 3,75 I 2 = - 20 ∠ - 30 °

- 2,42 ∠ - 75.97 ° + ( - 0,249 ∠ - 90 ° ) I 2 + 2 + j 3,75 I 2 = - 20 ∠ - 30 °

0,249 j + 2 + j 3,75 I 2 = - 17,32 - j 10 + 0,587 - j 2,35

I 2 = - 16,73 + j 7,65 2 + j 4

I 2 = 18,4 ∠ 155,43 ° 4,47 ∠ 63,43 °

I 2 = 4,12 ∠ 92 °     A

Passo 4

Substituindo o valor que encontramos para a corrente I 2 para encontrarmos I 1 , temos:

I 1 = 2,35 ∠ - 61,93 ° + 0,242 ∠ - 75,97 ° 4,12 ∠ 92 °

I 1 = 1,1 - j 2,07 + 0,99 ∠ 16,03 °

I 1 = 1,1 - j 2,07 + 0,95 + j 0,273

I 1 = 2,05 - j 1,797

I 1 = 2,73 ∠ - 41,24 °     A

Passo 5

Agora é só voltar para o domínio do tempo:

i 1 t = 2,73 cos ⁡ 4 t - 41,24 °   A

i 2 t = 4,12 cos ⁡ 4 t + 92 °   A

Resposta

i 1 t = 2,73 cos ⁡ 4 t - 41,24 °   A

i 2 t = 4,12 cos ⁡ 4 t + 92 °   A

Exercício Resolvido #7

Livro Sadiku, p.397, Problema 10.30

Use análise de malhas para determinar v 0 no circuito abaixo. Seja v 1 = 120 cos ⁡ 100 t + 90 °   V e v 2 = 80 cos ⁡ 100 t   V

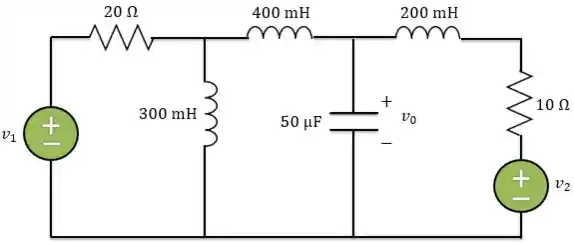
Passo 1

Primeiro, temos que passar o circuito para o domínio da frequência. Passando cada elemento, temos:

120 cos ⁡ ( 100 t + 90 ° )       →       120 ∠ 90 °   ,         ω = 100   r a d / s

80 cos ⁡ 100 t       →       80 ∠ 0 °   ,         ω = 100   r a d / s

400   m H       →       j ω L = j 40

300   m H       →       j ω L = j 30

200   m H       →       j ω L = j 20

50   µ F       →   -   j 1 ω C   = - j 200

Logo, o circuito no domínio da frequência é:

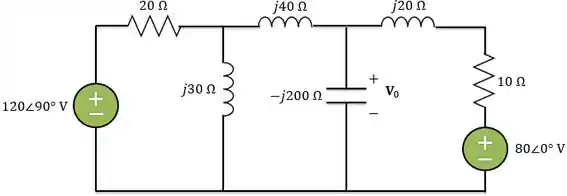
Passo 2

Agora, vamos preparar o circuito para utilizar a análise de malha:

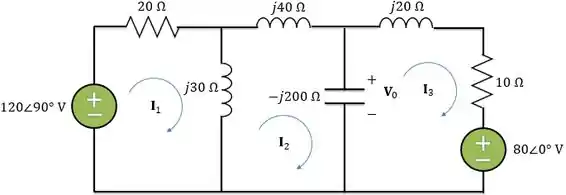
Pela lei de Ohm vemos que:

V 0 = - j 200 ( I 2 - I 3 )

Aplicando a LTK na malha 1:

- 120 ∠ 90 ° + 20 + j 30 I 1 - j 30 I 2 = 0

20 + j 30 I 1 - j 30 I 2 = j 120       ( i )

Aplicando a LTK na malha 2:

j 30 + j 40 - j 200 I 2 - j 30 I 1 - - j 200 I 3 = 0

- 30 I 1 - 130 I 2 + 200 I 3 = 0       ( i i )

Aplicando a LTK na malha 3:

- j 200 + j 20 + 10 I 3 - - 200 j I 2 + 80 ∠ 0 ° = 0

200 j I 2 + 10 - j 180 I 3 = - 80       ( i i i )

Passo 3

Então, precisamos resolver o sistema abaixo:

20 + j 30 I 1 - j 30 I 2 = j 120           ( i ) - 30 I 1 - 130 I 2 + 200 I 3 = 0               ( i i ) 200 j I 2 + 10 - j 180 I 3 = - 80   ( i i i )

Isolando I 1 na primeira equação, temos:

I 1 = j 120 + j 30 I 2 20 + j 30

I 1 = 120 ∠ 90 ° 36,05 ∠ 56,31 ° + 30 ∠ 90 ° 36,05 ∠ 56,31 ° I 2

I 1 = 3,33 ∠ 33,69 ° + 0,832 ∠ 33,69 °   I 2

Isolando I 3 na última equação, temos:

I 3 = - 80 - 200 j I 2 10 - j 180

I 3 = - 80 180,27 ∠ - 86,82 ° - 200 ∠ 90 ° 180,27 ∠ - 86,82 ° I 2

I 3 = - 80 180,27 ∠ - 86,82 ° - 200 ∠ 90 ° 180,27 ∠ - 86,82 ° I 2

I 3 = - 0,444 ∠ 86,82 ° - ( 1,11 ∠ 176,82 ° ) I 2

Substituindo I 1 e I 3 na equação ( i i ) , temos:

- 30 3,33 ∠ 33,69 ° + 0,832 ∠ 33,69 ° I 2 - 130 I 2 + 200 ( - 0,444 ∠ 86,82 ° - 1,11 ∠ 176,82 ° I 2 ) = 0

- 24,96 ∠ 33,69 ° I 2 - 130 I 2 - 222 ∠ 176,82 ° I 2 = 99,9 ∠ 33,69 ° + 88,8 ∠ 86,82 °

- 20,77 - j 13,84 - 130 + 221,66 - j 12,32 I 2 = 83,12 + j 55,41 + 4,93 + j 88,66

I 2 = 88,05 + j 144,07 70,89 - j 26,16

I 2 = 168,84 ∠ 58,57 ° 75,56 ∠ - 20,25 °

I 2 = 2,23 ∠ 78,82 °   A

Logo, na forma retangular I 2 será:

I 2 = 0,432 + j 2,187   A

Passo 4

Agora, vamos calcular I 3 utilizando o valor que encontramos para I 2 .

I 3 = - 0,444 ∠ 86,82 ° - ( 1,11 ∠ 176,82 ° ) I 2

I 3 = - 0,444 ∠ 86,82 ° - ( 1,11 ∠ 176,82 ° ) ( 2,23 ∠ 78,82 ° )

I 3 = - 0,0246 - j 0,443 - 2,475 ∠ 255,64 °

I 3 = - 0,0246 - j 0,443 + 0,614 + j 2,397

I 3 = 0,589 + j 1,954   A

Passo 5

Como já encontramos os valores de I 2 e I 3 , vamos substituí-los na equação abaixo:

V 0 = - j 200 ( I 2 - I 3 )

V 0 = - j 200 0,432 + j 2,187   - 0,589 + j 1,954

V 0 = - j 200 - 0,157 + j 0,233

V 0 = 200 ∠ - 90 ° 0,281 ∠ 123,97 °

V 0 = 56,2 ∠ 33,97 °   V

Passo 6

Para terminar, precisamos voltar para o domínio do tempo. Lembrando que ω = 100   r a d / s , temos:

v 0 t = 56,2 cos ⁡ 100 t + 33,97 °   V

Resposta

v 0 t = 56,2 cos ⁡ 100 t + 33,97 °   V

Exercício Resolvido #8

Livro Sadiku, Exemplo 10.2

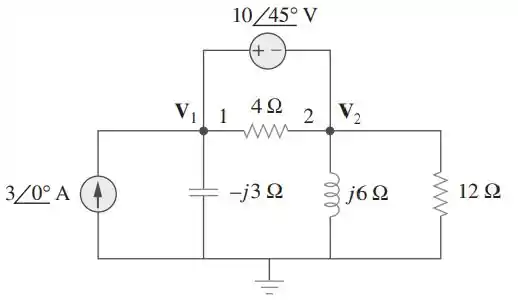
Calcule V 1 e V 2 no circuito da figura.

Passo 1

Vamos começar analisando os nós 1 e 2. Nós aí vemos que existe uma fonte de tensão entre dois nós, ou seja, formam um supernó como o da figura:

Passo 2

Agora, vamos aplicar a LKC a esse supernó, e chegamos em:

3   =   V 1 - j 3 +   V 2 j 6 +   V 2 12

ou

36 = j 4 V 1 + ( 1 - j 2 ) V 2

Passo 3

Agora, vamos analisar a fonte de tensão que está ligada entre os nós 1 e 2, de modo que

V 1 = V 2 + 10 ∠ 45 °

Substituindo esse V 1 na equação do Passo 2, achamos o V 2 :

36 - 40 ∠ 135 ° = ( 1 + j 2 ) V 2   ⇒ V 2 = 31.41 ∠ - 87.18 ° V

(Note que transformamos o j 4 V 2 em polar   4 ∠ 90 ° )

Agora, achamos o V 1 :

V 1 = V 2 + 10 ∠ 45 ° = 25.78 ∠ - 70.48 °

Resposta

V 1 = 25.78 ∠ - 70.48 ° V

V 2 = 31.41 ∠ - 87.18 ° V

Exercício Resolvido #9

Livro Sadiku, Problema 10.5

Determine i o no circuito da Figura

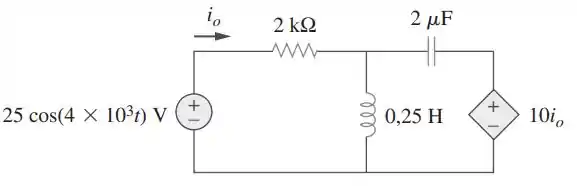
Passo 1

Vamos começar passando as nossas impedâncias para o domínio da frequência:

Analisando nossa fonte, vemos que ω = 4 × 10 - 3

Para o indutor com indutância de 0.25 H :

j ω L   =   j ( 4 × 10 - 3 )0.25

j ω L   =   j 1000

Para o capacitor com capacitância de 2 μ F :

1 j ω C   =   1 j ( 4 × 10 3 ) ( 2 μ F )

1 j ω C   =   1 j ( 10 3 ) ( 8 × 10 - 6 F )

1 j ω C   =   - j 1000 8

1 j ω C   =   - j 125

Passo 2

Agora vamos redesenhar o circuito:

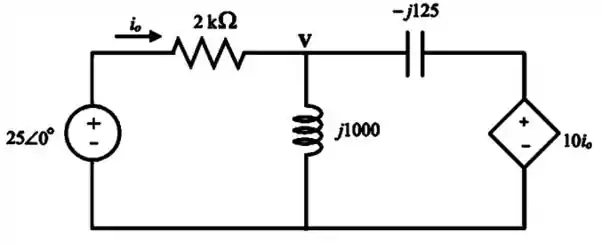
Passo 3

Vamos aplicar a Lei das Correntes de Kirchhoff ao nó V.

V j 1000 + V - 10 i o - j 125 - i o = 0

V j 1000 - V j 125 + 10 i o j 125 = i o

V ( 1 j 1000 - 1 j 125 ) - 10 i o j 125 = i o

V ( j 7 × 10 - 3 ) = ( 125 + j 10 ) i o 125

V = ( 125 + j 10 ) i o 125 ( j 7 × 10 - 3 )

V = ( 125 + j 10 ) i o j 0.875

V = ( 11.42 - j 142.8 ) i o

Passo 4

Agora, vamos calcular a corrente i o utilizando a Primeira Lei de Ohm:

i o = 25 ∠ 0 ° - V 2 k Ω

i o = 25 ∠ 0 ° - ( 11.42 - j 142.8 ) i o 2 k Ω

i o ( 2 k Ω ) = 25 - ( 11.42 - j 142.8 ) i o

i o ( 2000 + 11.42 - j 142.8 ) = 25

i o = 25 ( 2011.42 - j 142.8 )

i o = 0.012 + j 0.0008777

i o = 0.012 ∠ 4.179 °

Resposta

i o = 0.012 ∠ 4.179 °

Exercício Resolvido #10

Livro Sadiku, Problema 10.20

Se v s ( t ) = V m s e n ω t   e v o ( t ) = A s e n ( ω t + ϕ ) ,deduza as expressões para A e ϕ .

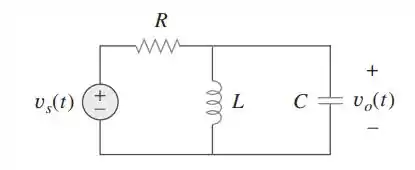
Passo 1

Aqui, vamos começar desenhando nosso circuito novamente no domínio da frequência e mostrando nossa tensão na forma fasorial. Perceba que o resistor continua sendo R, o indutor passa a ser j ω L e o capacitor passa a ser 1 j ω C

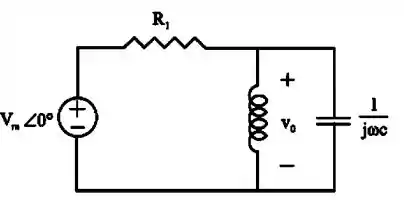
Passo 2

Agora, vamos calcular a impedância em paralelo:

Z = j ω L / / 1 j ω C

Z = L C j ω L + 1 j ω C = j ω L 1 - ω 2 L C

Em seguida, a gente acha a nossa tensão V o que é aquela em cima do indutor (ou em cima do capacitor, as duas são iguais pois estão em paralelo)

V o   =   V m   Z R + Z

V o   =   V m   j ω L 1 - ω 2 L C R + j ω L 1 - ω 2 L C

V o   = j ω L   × V m R ( 1 - ω 2 L C ) + j ω L

V o   = ω L V m R ( 1 - ω 2 L C ) 2 + ω L 2   ∠ ( 90 ° - t a n - 1 ω L R ( 1 - ω 2 L C ) )

Passo 3

Então, agora basta comparar com os dados do enunciado. Como temos v o ( t ) = A s e n ( ω t + ϕ ) , isso é a tensão que achamos só que no domínio do tempo. Se colocar no domínio da frequência, teremos V o   = A ∠ ϕ ° .

Comparando…

V o   = ω l V m R ( 1 - ω 2 L C ) 2 + ω L 2   ∠ ( 90 ° - t a n - 1 ω L R ( 1 - ω 2 L C ) )   =   A ∠ ϕ °

A   = ω L V m R ( 1 - ω 2 L C ) 2 + ω L 2

  ϕ = 90 ° - t a n - 1 ω L R ( 1 - ω 2 L C )

Resposta

A   = ω L V m R ( 1 - ω 2 L C ) 2 + ω L 2

  ϕ = 90 ° - t a n - 1 ω L R ( 1 - ω 2 L C )

Exercícios de Livros Relacionados

O fasor corrente Ib, no circuito da Figura P9.36, é 25 ∠0 º º mA.. a) Determine Ia, Ic e Ig. b) Se v = 1.500 rad/s, determine as expressões para i a(t), i c (t) e i g(t).
No circuito da Figura 10.46, a corrente i(t) é: 10 cos ⁡ tA b) 10 s e ntA c) 5 cos ⁡ tA d) 5s e ntA e) 4.472 cos ⁡ t - 63.43 ° A
Usando a Figura 10.51, elabore um problema para ajudar outros estudantes a entender melhor a análise nodal.
Use o PSpice ou MultiSim para determinar V o no circuito da Figura 10.124. Suponha v = 1r a d / s .
Usando a Figura 10.127 , elabore um problema para ajudar outros estudantes a entender melhor como realizar a análise C A com o PSpice ou MultiSim.