Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Circuito RLC sem fonte

Ver Todos os Exercícios

Teoria

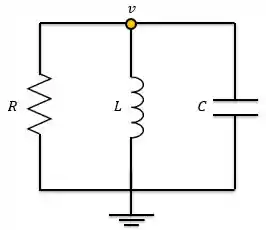
Até agora a gente sabe como resolver circuitos com resistores associados com capacitor e circuitos de resistores com Indutor. Mas e se fosse o circuito abaixo? Como encontraríamos tensões e correntes?

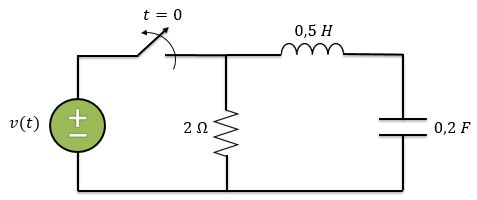
É isso que vamos aprender. Estudaremos circuitos que possuem resistores, capacitores e indutores. Esses circuitos são conhecidos como circuitos de segunda ordem, pois as equações diferenciais que encontraremos para descrevê-los terão segundas derivadas.

Determinação dos valores iniciais e finais

O primeiro passo para determinar a corrente e a tensão de circuitos de segunda ordem é determinar as condições iniciais e finais da tensão do capacitor v C , da corrente no indutor i L e de suas respectivas derivadas. Vamos fazer um exemplo para ficar mais claro.

No circuito abaixo, a chave ficou fechada por um longo tempo e em t = 0 ela se abre. Queremos encontrar os valores iniciais e finais, ou seja, determinar v C 0 + , i L 0 + , d v C ( 0 + ) / d t , d i L ( 0 + ) / d t , i L ∞ e v C ∞ .

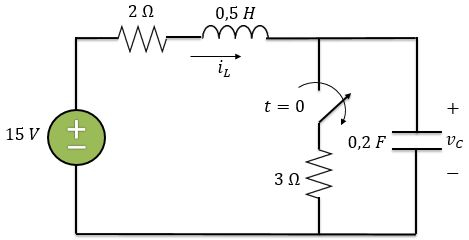
Bora começar! Como a chave estava fechada por um longo tempo antes de t = 0 , o circuito já estava em seu regime permanente, ou seja, já podemos considerar o indutor funcionando como curto-circuito e o capacitor como um circuito aberto.

Logo, para o instante exatamente antes da chave se abrir ( t = 0 - ) , a gente pode considerar o circuito assim:

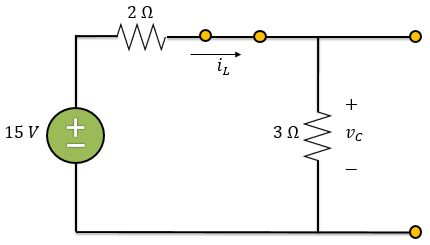
Como a corrente só circula por caminhos fechados, pela lei de Ohm, temos:

i L 0 - = 15 2 + 3 = 3   A  

Logo,

v C 0 - = 3 i L 0 - = 9   V

Lembrando que a corrente no indutor e a tensão no capacitor não variam instantaneamente,

i L 0 + = i L 0 - = 3   A

e

v C 0 + = v C 0 - = 9   V

Agora, vamos analisar o circuito quando a chave abre. Em t = 0 + , podemos considerar o seguinte circuito:

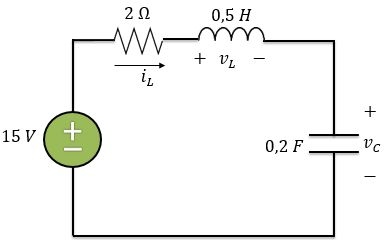
Como o circuito está em série, a corrente é a mesma para todo o circuito, ou seja, a corrente no indutor é igual à corrente no capacitor. Logo, no capacitor temos:

i L 0 + = 0,2 d v C 0 + d t

3 = 0,2 d v C 0 + d t

d v C 0 + d t = 3 0,2 = 15   V / s

Vamos agora encontrar d i L ( 0 + ) / d t . Para isso, vamos aplicar a LTK no circuito.

- 15 + 2 i L 0 + + v L 0 + + v C 0 + = 0

Simplificando,

v L 0 + = 15 - 6 - 9 = 0

Como,

v L 0 + = 0,5 d i L 0 + d t

0 = 0,5 d i L 0 + d t

Logo,

d i L 0 + d t = 0   A / s  

Falta encontrarmos i L ∞ e v C ∞ . Quando t → ∞ , o circuito atinge o regime permanente mais uma vez e o indutor funciona como um curto-circuito e o capacitor como um circuito aberto. Logo, o circuito fica assim:

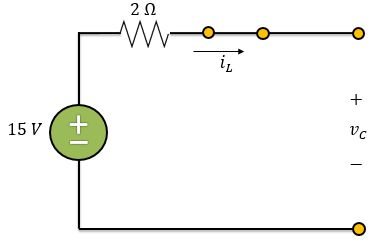
Como o circuito acima está aberto, não há circulação de corrente e, consequentemente, não há queda de tensão no resistor. Portanto:

i L ∞ = 0   A         e       v C ∞ = 15   V

Pronto! Descobrimos todos os valores iniciais e finais desse circuito.

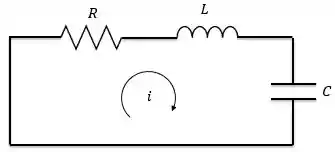
Circuito RLC série sem fonte

Agora vamos analisar a resposta natural do circuito RLC série sem fonte, mostrado no circuito abaixo. O circuito está inicialmente energizado, sendo que V 0   é a tensão inicial do capacitor e I 0 a corrente inicial do indutor.

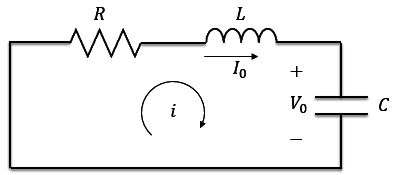
Aplicando a LTK no circuito, temos:

R i + L d i d t + 1 C ∫ - ∞ t i   d t = 0

Vamos eliminar a integral derivando a equação em relação a t .

R d i d t + L d 2 i d t 2 + 1 C i = 0

Agora, vamos dividir os termos por L e arrumar a equação.

d 2 i d t 2 + R L d i d t + i L C = 0

Chegamos na equação diferencial de segunda ordem. Para resolver essa equação, primeiro vamos obter a equação característica:

r 2 + R L r + 1 L C = 0

Resolvendo a equação do segundo grau, temos as duas raízes

r 1 = - R 2 L + R 2 L 2 - 1 L C

r 2 = - R 2 L - R 2 L 2 - 1 L C

É muito comum essas raízes serem escritas assim:

r 1 = - α + α 2 - ω 0 2

r 2 = - α - α 2 - ω 0 2

Onde,

α = R 2 L               e             ω 0 = 1 L C

Chamamos α de fator de amortecimento e ω 0 de frequência de ressonância ou de frequência natural não-amortecida.

Beleza! Até agora tá show. Mas como vai ser a solução da EDO de segunda ordem em função desses parâmetros?

Teremos três tipos de solução:

  1. Se α > ω 0 , temos o caso superamortecido;
  2. Se α = ω 0 , temos o caso de amortecimento crítico;
  3. Se α < ω 0 , temos o caso subamortecido.

Vamos agora analisar cada caso desse separadamente.

Superamortecido → α > ω 0

Analisando as raízes

r 1 = - α + α 2 - ω 0 2

r 2 = - α - α 2 - ω 0 2

Quando α > ω 0 , que é equivalente a:

R 2 L > 1 L C

C > 4 L R 2

As raízes r 1 e r 2 serão reais, negativas e distintas. Logo, a solução da EDO será:

i t = A e r 1 t + B e r 2 t  

Sendo A e B constantes.

Logo, a corrente vai decair ao longo do tempo e vai se aproximando de zero, como no gráfico abaixo:

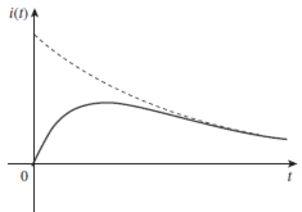
Amortecimento crítico → α = ω 0

Analisando as raízes

r 1 = - α + α 2 - ω 0 2

r 2 = - α - α 2 - ω 0 2

Quando α = ω 0 , que é equivalente a C = 4 L / R 2 , as raízes r 1 e r 2 serão reais e iguais:

r 1 = r 2 = - α = R 2 L

Logo, a solução da EDO de segunda ordem para raízes iguais será:

i t = A e - α t + B t e - α t  

i t = A + B t e - α t

Sendo A e B constantes.

Logo, a resposta natural para esse caso pode ser caracterizada como o gráfico abaixo:

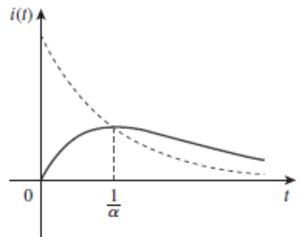
Subamortecido → α < ω 0

Analisando as raízes

r 1 = - α + α 2 - ω 0 2

r 2 = - α - α 2 - ω 0 2

Quando α < ω 0 , que é equivalente a C < 4 L / R 2 , as raízes r 1 e r 2 terão raiz quadrada de número negativo:

r 1 = - α + - ω 0 2 - α 2 = - α + j ω d

r 2 = - α - - ω 0 2 - α 2 = - α - j ω d

Onde j = - 1 e ω d = ω 0 2 - α 2 , que é chamada de frequência natural amortecida.

Logo, a solução da EDO de segunda ordem para o caso subamortecido será:

i t = A e - ( α - j ω d ) t + B e - ( α + j ω d ) t

i t = e - α t A e j ω d t + B e - j ω d t

Chegamos a uma solução, mas esse tanto de exponenciais dificulta a nossa análise de como é essa resposta natural. Por isso, a gente usa a identidade de Euler:

e j θ = cos ⁡ θ + j sin ⁡ θ ,

e - j θ = cos ⁡ θ - j sin ⁡ θ

Portanto, a nossa solução fica assim:

i t = e - α t [ A ( cos ⁡ ω d t + j sin ⁡ ω d t ) + B cos ⁡ ω d t - j sin ⁡ ω d t )

i t = e - α t [ A + B cos ⁡ ω d t + j A - B sin ⁡ ω d ]

Substituindo as constantes A + B pela constante D e j A - B pela constante F , temos

i t = e - α t ( D cos ⁡ ω d t + F sin ⁡ ω d t )

Logo, vemos a presença de funções seno e cosseno, mostrando que a resposta natural para este caso decresce exponencialmente e é oscilatória. Como podemos ver no gráfico abaixo:

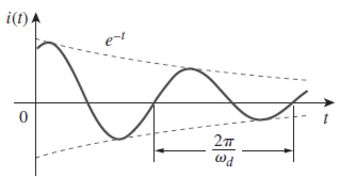
Antes de estudarmos o circuito RLC paralelo sem fonte, vamos fazer um exemplo para entender melhor o que estudamos.

Vamos calcular as raízes do polinômio característico do circuito abaixo e ver qual o tipo de resposta natural ele tem.

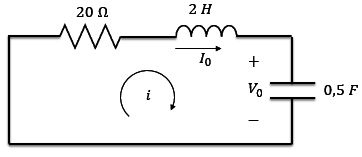
O primeiro passo é encontrar fator de amortecimento α e a frequência natural não-amortecida ω 0 .

α = R 2 L = 20 2 2 = 5

ω 0 = 1 L C = 1 2 × 0,5 = 1

Como α > ω 0 , a resposta é superamortecida.

As raízes são

r 1 = - α + α 2 - ω 0 2

r 1 = - 5 + 25 - 1 = - 0,101

e

r 2 = - α - α 2 - ω 0 2

r 2 = - 5 - 5 2 - 1 = - 9,899

Pelos valores encontrados para as raízes, também podemos concluir que o circuito tem resposta superamortecida, já que as raízes são reais negativas e diferentes.

Circuito RLC paralelo sem fonte

Vamos considerar agora o circuito RLC paralelo sem fonte abaixo, em que o circuito está inicialmente energizado. Sendo V 0   a tensão inicial do capacitor e I 0 a corrente inicial do indutor, tem-se:

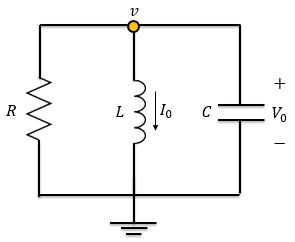
Os três elementos do circuito têm a mesma tensão v , porque estão ligados em paralelo. Aplicando LCK ao nó, temos:

v R + 1 L ∫ - ∞ t v   d t + C d v d t = 0

Vamos eliminar a integral derivando a equação em relação a t :

d 2 v d t 2 + 1 R C d v d t + 1 L C v = 0

Chegamos na equação diferencial de segunda ordem. Então, vamos obter a equação característica:

r 2 + 1 R C r + 1 L C = 0

Resolvendo a equação do segundo grau, temos as duas raízes

r 1 = - 1 2 R C + 1 2 R C 2 - 1 L C

r 2 = - 1 2 R C - 1 2 R C 2 - 1 L C

Podendo ser escritas assim:

r 1 = - α + α 2 - ω 0 2

r 2 = - α - α 2 - ω 0 2

Onde,

α = 1 2 R C               e             ω 0 = 1 L C

Mais uma vez teremos três tipos de solução. Vamos agora analisar cada caso separadamente.

Superamortecido → α > ω 0

Analisando as raízes

r 1 = - α + α 2 - ω 0 2

r 2 = - α - α 2 - ω 0 2

Quando α > ω 0 , que é equivalente a

1 2 R C > 1 L C

L > 4 R 2 C

As raízes r 1 e r 2 serão reais negativas e distintas. Logo, a solução da EDO será

v t = A e r 1 t + B e r 2 t  

Sendo A e B constantes.

Amortecimento crítico → α = ω 0

Analisando as raízes

r 1 = - α + α 2 - ω 0 2

r 2 = - α - α 2 - ω 0 2

Quando α = ω 0 , que é equivalente a L = 4 R 2 C ,   as raízes r 1 e r 2 serão reais e iguais:

r 1 = r 2 = - �� = - 1 2 R C = - 1 L C

Logo, a solução da EDO de segunda ordem para raízes iguais será:

v t = A e - α t + B t e - α t  

v t = A + B t e - α t

Sendo A e B constantes.

Subamortecido → α < ω 0

Analisando as raízes

r 1 = - α + α 2 - ω 0 2

r 2 = - α - α 2 - ω 0 2

Quando α < ω 0 , que é equivalente a C < 4 L / R 2 , as raízes r 1 e r 2 terão raiz quadrada de número negativo:

r 1 = - α + - ω 0 2 - α 2 = - α + j ω d

r 2 = - α - - ω 0 2 - α 2 = - α - j ω d

Onde j = - 1 e ω d = ω 0 2 - α 2 , que é chamada de frequência natural amortecida.

Logo, a solução da EDO de segunda ordem para o caso subamortecido será:

v t = e - α t ( A cos ⁡ ω d t + B sin ⁡ ω d t )

Lembrando que todas as constantes são determinadas pelas nossas condições finais e iniciais.

Agora é exercitar!

Circuito RLC série sem fonte

Circuito RLC paralelo sem fonte

Exercícios Resolvidos

Exercício Resolvido #1

Livro Sadiku, p.320, Problema 8.7

Um circuito R L C em série possui R = 20   k Ω ,   L = 0,2   m H   e   C = 5   µ F . Que tipo de amortecimento é apresentado pelo circuito?

Passo 1

De acordo com o enunciado, temos o seguinte circuito:

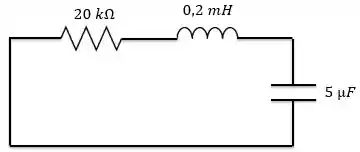
Passo 2

Agora vamos encontrar o fator de amortecimento α e a frequência natural não-amortecida ω 0 .

α = R 2 L

α = 20 × 10 3 2 0,2 × 10 - 3 = 50 × 10 6

e

ω 0 = 1 L C

ω 0 = 1 0 , 2 × 10 - 3 5 × 10 - 6 = 31622,77

Como α > ω 0 , a resposta é superamortecida.

Resposta

Superamortecido

Exercício Resolvido #2

Livro Sadiku, p.321, Problema 8.12

Se R = 50 Ω ,   L = 1,5   H , qual valor de C tornará um circuito RLC em série:

( a ) com amortecimento supercrítico

( b ) com amortecimento crítico

c com subamortecimento

Passo 1

Em um circuito R L C série sabemos que:

α = R 2 L           e         ω 0 = 1 L C  

Passo 2

Para o caso superamortecido, temos a condição de que α > ω 0 .

Logo,

R 2 L > 1 L C

C > 4 L R 2

Substituindo os valores do resistor e do indutor,

C > 4 1,5 50 2

C > 0,0024   F

Passo 3

Para o caso do circuito RLC em série com amortecimento crítico, temos a condição de α = ω 0 .

Logo,

R 2 L = 1 L C

C = 4 L R 2

C = 4 1,5 50 2

C = 0,0024   F

Passo 4

E para o caso de subamortecimento, temos que α < ω 0 .

Logo,

R 2 L < 1 L C

C < 4 L R 2

C < 4 1,5 50 2

C < 0,0024   F

Resposta

a     C > 0,0024   F

b     C = 0,0024   F

a     C < 0,0024   F

Exercício Resolvido #3

Elaboração própria

Dado o circuito abaixo, diga o tipo de amortecimento:

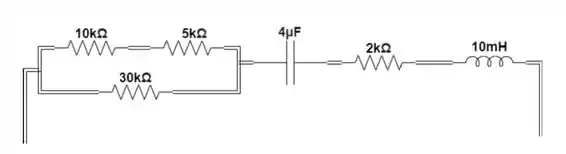
Passo 1

Primeiro devemos lembrar as fórmulas de α e ω :

α =   R 2 L

e ω =   1 L C

Passo 2

Para calcular o R e q faremos a relação série entre 10 k Ω e 5 k Ω :

R 1 = 10 k + 5 k = 15 k Ω

Depois esse resistor estará em paralelo com o resistor de 30 k Ω :

R 2 = R 1 * 30 k R 1 + 30 k

R 2 = 15 k * 30 k 15 k + 30 k = 10 k Ω

E por fim teremos uma associação série com o resistor de 2 k Ω :

R e q =   R 2 + 2 k = 10 k   + 2 k   =   12 k Ω  

Passo 3

Calculo de α :

α = R 2 L = 12 k 2 * 10 m = 600 * 10 3

Passo 4

Calculo de ω :

ω =   1 L C = 1 4 * 10 - 6 * 10 * 10 - 3 = 5000

Passo 5

Como α >   ω , sabemos que se trata de um circuito superamortecido.

Resposta

Circuito superamortecido.

Exercício Resolvido #4

Livro Sadiku, p.321, Problema 8.13

Para o circuito abaixo, calcule o valor de R necessário para se obter uma resposta com amortecimento crítico.

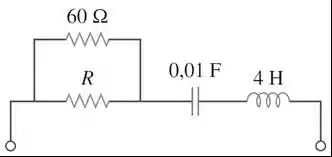
Passo 1

Para que o amortecimento seja crítico, temos a condição de que α = ω 0 . Então, primeiro temos que calcular α e ω 0 . Em um circuito R L C série sabemos que:

α = R 2 L           e         ω 0 = 1 L C  

Passo 2

Como os resistores estão associados em paralelo, precisamos calcular a resistência equivalente.

R e q = 60   ×   R 60 + R

Passo 3

Logo, o fator de amortecimento será

α = R e q 2 L

Como L = 4   H ,

α = R e q 2 4 = R e q 8

Passo 4

Agora, vamos calcular a frequência natural não amortecida ω 0 .

ω 0 = 1 4 × 0,01

ω 0 = 5  

Passo 5

Como no amortecimento crítico α = ω 0 , temos

R e q 8 = 5

R e q = 40   Ω

Passo 6

Agora que temos o valor da resistência equivalente é só substituir para encontrar o valor de R .

R e q = 60   ×   R 60 + R

40 = 60   ×   R 60 + R

Logo,

60 R = 2400 + 40 R

20 R = 2400

R = 120   Ω

Resposta

R = 120   Ω

Exercício Resolvido #5

Livro Sadiku, p.322, Problema 8.23

Para o circuito abaixo, que valor de C é necessário para tornar a resposta subamortecida com fator de amortecimento unitário α = 1 ?

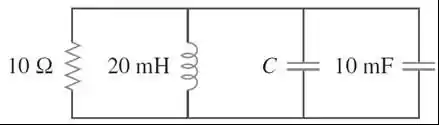
Passo 1

Para que o amortecimento seja subamortecido, temos a condição de que α < ω 0 e em um circuito R L C paralelo sabemos que:

α = 1 2 R C           e         ω 0 = 1 L C    

Passo 2

Como os capacitores estão associados em paralelo, precisamos calcular a capacitância equivalente. Lembrando que quando os capacitores estão associados em paralelo, a capacitância equivalente é a soma dos valores de cada capacitor.

C e q = C + 0,01

Passo 3

Logo, como fator de amortecimento é unitário

α = 1 2 R C e q = 1

Como R = 10   Ω ,

1 = 1 2 ( 10 ) C e q

C e q = 1 20 = 0,05   F

Passo 4

Agora, vamos calcular a frequência natural não amortecida ω 0 .

ω 0 = 1 L C e q

ω 0 = 1 0,02 × 0,05

ω 0 = 31,62

Portanto, α < ω 0 , ou seja, a capacitância equivalente calculada está de acordo com a condição subamortecida.

Passo 5

Substituindo o valor de C e q encontramos o valor do capacitor que queremos.

C e q = C + 0,01

0,05 = C + 0,01

C = 0,04   F

C = 40   m F

Resposta

C = 40   m F

Exercício Resolvido #6

Livro Sadiku, p.320, Problema 8.9

A corrente em um circuito R L C é descrita por

d 2 i d t 2 + 10 d i d t + 25 i = 0

Se i 0 = 10   A e d i ( 0 ) / d t = 0 determine i ( t ) para t > 0 .

Passo 1

Como o enunciado falou da corrente em um circuito R L C , significa que a mesma corrente passa por todos os elementos. Portanto, o circuito é um R L C série.

Passo 2

O enunciado disse que a corrente é descrita assim

d 2 i d t 2 + 10 d i d t + 25 i = 0

Vamos encontrar a solução de EDO de segunda ordem. Ela possui a seguinte equação característica:

r 2 + 10 r + 25 = 0

Logo,

r 1,2 = - 10 ± 10 2 - 4 × 1 × 25 2 ( 1 )

Então,

r 1 = - 10 + 100 - 100 2 = - 5

r 2 = - 10 - 100 - 100 2 = - 5

Passo 3

Temos duas raízes reais e iguais, r 1 = r 2 = - α = - 5 . Logo, para esse caso a solução da EDO é

i t = A + B t e - α t

Substituindo o valor de α

i t = A + B t e - 5 t

Passo 4

Agora, precisamos encontrar os valores das constantes A e B . Para isso, vamos utilizar as nossas condições iniciais

i 0 = 10   A

d i 0 d t = 0

Da primeira condição,

i 0 = A + B 0 e - 5 ( 0 ) = 10

A = 10

Passo 5

Calculando a derivada de i ( t ) , temos:

d i t d t = B e - 5 t + A + B t - 5 e - 5 t

Usando a nossa segunda condição inicial,

d i 0 d t = B e - 5 0 + A + B 0 - 5 e - 5 0 = 0

B - 5 A = 0

B = 5 10

B = 50

Passo 6

Portanto, substituindo os valores das constantes, nossa solução final será

i t = 10 + 50 t e - 5 t   A

Resposta

i t = 10 + 50 t e - 5 t   A

Exercício Resolvido #7

Livro Sadiku, p.320, Problema 8.9

A equação diferencial que descreve a tensão em um circuito R L C é

d 2 v d t 2 + 5 d v d t + 4 v = 0

Dado que v 0 = 0 e d v ( 0 ) / d t = 10   V / s , obtenha v ( t ) .

Passo 1

Como o enunciado falou da tensão em um circuito R L C , significa que todos os elementos têm a mesma tensão. Portanto, o circuito é um R L C paralelo.

Passo 2

O enunciado disse que a tensão no circuito é descrita assim

d 2 v d t 2 + 5 d v d t + 4 v = 0

Vamos encontrar a solução de EDO de segunda ordem. Ela possui a seguinte equação característica:

r 2 + 5 r + 4 = 0

Logo,

r 1,2 = - 5 ± 5 2 - 4 × 1 × 4 2 ( 1 )

Então,

r 1 = - 5 + 25 - 16 2

r 1 = - 5 + 3 2 = - 1

e

r 2 = - 5 - 25 - 16 2

r 2 = - 5 - 3 2 = - 4

Passo 3

Temos duas raízes reais negativas e distintas. Logo, para esse caso a solução da EDO é

v t = A e r 1 t + B e r 2 t

Substituindo os valores das raízes

v t = A e - t + B e - 4 t

Passo 4

Agora, precisamos encontrar os valores das constantes A e B . Para isso, vamos utilizar as nossas condições iniciais:

v 0 = 0

d v 0 d t = 10

Da primeira condição,

v 0 = A e - ( 0 ) + B e - 4 ( 0 ) = 0

A + B = 0

Passo 5

Calculando a derivada de v ( t ) , temos:

d v t d t = - A e - t - 4 B e - 4 t

Usando a nossa segunda condição inicial,

d v 0 d t = - A e - ( 0 ) - 4 B e - 4 ( 0 ) = 10

- A - 4 B = 10

Passo 6

Chegamos no seguinte sistema:

A + B = 0   - A - 4 B = 10

Isolando B na primeira equação e substituindo na segunda, temos

- A - 4 - A = 10

3 A = 10

A = 10 3

Logo,

B = - A = - 10 3

Passo 7

Portanto, substituindo os valores das constantes, nossa solução final será:

v t = 10 3 e - t - 10 3 e - 4 t     V

Resposta

v t = 10 3 ( e - t - e - 4 t )     V

Exercício Resolvido #8

Livro Sadiku, p.321, Problema 8.16

Determine i t para t > 0 no circuito abaixo.

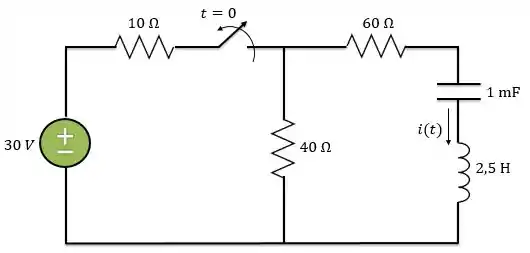
Passo 1

Vamos considerar que a chave estava fechada por um longo tempo antes de t = 0 . Logo, o circuito já estava em seu regime permanente, ou seja, já podemos considerar o indutor funcionando como curto circuito e o capacitor como um circuito aberto.

Passo 2

Logo, para o instante exatamente antes da chave se abrir ( t = 0 - ) , a gente pode considerar o circuito assim:

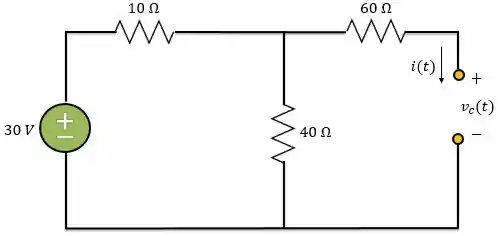
Como o circuito está aberto, não há circulação de corrente.

i 0 - = 0

Além disso, a tensão nos terminais do capacitor v c será a tensão nos terminais do resistor de 40   Ω .

v c 0 - = 40 40 + 10 × 30

v c 0 - = 24   V

Passo 3

Agora, vamos analisar o circuito quando a chave abre. Em t = 0 + , podemos considerar o seguinte circuito:

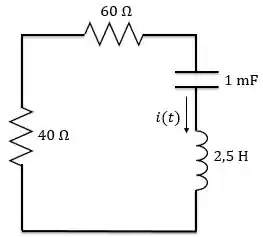
Esse circuito nós conhecemos! É o R L C série sem fonte!

Sendo R a soma dos resistores, já que estão em série.

Temos duas maneiras de encontrar a expressão para corrente i ( t ) . Vamos fazer das duas formas e você escolhe depois a que considerar melhor.

Aplicando a LTK no circuito, temos:

R i + L d i d t + 1 C ∫ - ∞ t i   d t = 0

Vamos eliminar a integral derivando a equação em relação a t .

R d i d t + L d 2 i d t 2 + 1 C i = 0

Agora, vamos dividir os termos por L e arrumar a equação.

d 2 i d t 2 + R L d i d t + i L C = 0

Substituindo os valores dos elementos, temos:

d 2 i d t 2 + 100 2,5 d i d t + i ( 0,001 ) ( 2,5 ) = 0

d 2 i d t 2 + 40 d i d t + 400 i = 0

Passo 4

Chegamos na equação diferencial de segunda ordem. Para resolver essa equação, primeiro vamos obter a equação característica:

r 2 + 40 r + 400 = 0

Resolvendo a equação do segundo grau, temos as duas raízes

r 1 = - 40 + 40 2 - 1600 2

r 1 = - 40 + 0 2

r 1 = - 20

e

r 2 = - 40 - 0 2

r 2 = - 20

Portanto, temos duas raízes reais, iguais e negativas:

r 1 = r 2 = - 20

Para esse caso a solução da EDO é

i t = A + B t e r 1 t

i t = A + B t e - 20 t

Essa é a primeira maneira!

Passo 5

Agora, vamos fazer de uma outra maneira mais rápida. Sabemos que em um circuito R L C série sem fontes:

α = R 2 L               e             ω 0 = 1 L C

Substituindo os valores dos elementos, temos:

α = 100 2 × 2,5 = 20

e

ω 0 = 1 ( 0,001 ) ( 2,5 ) = 20

Como α = ω 0 , temos o caso de amortecimento crítico e para esse caso a expressão da corrente é:

i t = A + B t e - α t

Substituindo o valor de α ,

i t = A + B t e - 20 t

Pronto! Essa é a segunda maneira.

Passo 6

Agora, precisamos encontrar os valores das constantes A e B . Como se trata de uma EDO de segunda ordem, precisamos da condição inicial da corrente i ( 0 + ) e de sua derivada d i ( 0 + ) / d t .

Nós já calculamos que:

i 0 - = 0

Como no indutor a corrente não varia instantaneamente, então:

i 0 - = i 0 + = 0

Portanto,

i 0 + = A + B ( 0 ) e - 20 ( 0 )

A = 0

Como o circuito é serie, a corrente é a mesma para todo o circuito e como no capacitor a tensão não pode variar instantaneamente:

v c 0 - = v c 0 + = 24   V

Logo, no indutor temos:

v L 0 + = L d i ( 0 + ) d t

Aplicando a LTK no circuito, temos:

R i 0 + + v c 0 + + v L 0 + = 0

v L 0 + = - v c 0 + - R i ( 0 + )

v L 0 + = - 24 - 100 0

v L 0 + = - 24   V

Isolando d i ( 0 + ) / d t ,

d i 0 + d t = 1 2,5 ( - 24 )

d i 0 + d t = - 9,6

Passo 7

Agora, vamos derivar a nossa expressão para a corrente do circuito.

i t = A + B t e - 20 t

Já sabemos que A = 0 . Logo,

i t = B t e - 20 t

Então, pela regra do produto, temos:

d i t d t = B e - 20 t + B t e - 20 t ( - 20 )

d i t d t = B e - 20 t - 20 B t e - 20 t

Usando a condição inicial para a derivada da corrente:

d i 0 + d t = B e - 20 ( 0 ) - 20 B 0 e - 20 0 = - 9,6

B = - 9,6

Passo 8

Portanto, substituindo os valores das constantes, nossa solução final será:

i t = 0 + ( - 9,6 ) t e - 20 t

i t = - 9,6 t e - 20 t     A

Resposta

i t = - 9,6 t e - 20 t     A

Exercício Resolvido #9

Livro Sadiku, p.321, Problema 8.14

A chave do circuito abaixo muda da posição A para B em t = 0 (observe atentamente que a chave deve se conectar ao ponto B antes de ela desfazer a conexão em A , um interruptor). Fazendo v 0 = 0 ,   determine v ( t ) para t > 0 .

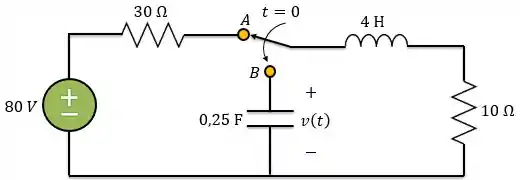
Passo 1

Vamos considerar que a chave estava na posição A por um longo tempo antes de t = 0 . Logo, o circuito já estava em seu regime permanente, ou seja, já podemos considerar o indutor funcionando como curto-circuito e o capacitor como um circuito aberto.

Passo 2

Logo, para o instante exatamente antes da chave se abrir ( t = 0 - ) , a gente pode considerar o circuito assim:

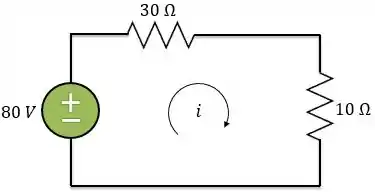
Logo, pela lei de Ohm a corrente será

i 0 - = 80 40

i 0 + = 2   A

Passo 3

Agora, vamos analisar o circuito quando a chave muda para posição B . Em t = 0 + , podemos considerar o seguinte circuito:

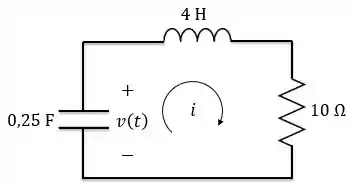
Repare que v e i não estão de acordo com a convenção de sinais dos elementos passivos, lembra? Então, para ficar mais fácil da gente resolver, vamos inverter a polaridade da tensão e chama-la de v 1 .

Onde,

v t = - v 1 ( t )

Logo, teremos o seguinte circuito:

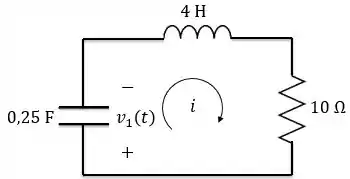
Esse circuito nós conhecemos! É o R L C série sem fonte. Aplicando a LTK no circuito, temos:

R i + L d i d t + 1 C ∫ - ∞ t i   d t = 0

Vamos eliminar a integral derivando a equação em relação a t .

R d i d t + L d 2 i d t 2 + 1 C i = 0

Agora, vamos dividir os termos por L e arrumar a equação.

d 2 i d t 2 + R L d i d t + i L C = 0

Substituindo os valores dos elementos, temos:

d 2 i d t 2 + 10 4 d i d t + i ( 0,25 ) ( 4 ) = 0

d 2 i d t 2 + 2,5 d i d t + i = 0

Passo 4

Chegamos na equação diferencial de segunda ordem. Para resolver essa equação, primeiro vamos obter a equação característica:

r 2 + 2,5 r + 1 = 0

Resolvendo a equação do segundo grau, temos as duas raízes

r 1 = - 2 , 5 - 2,5 2 - 4 2

r 1 = - 2,5 - 1,5 2

r 1 = - 2

e

r 2 = - 2,5 + 1,5 2

r 2 = - 0,5

Temos duas raízes reais negativas e distintas. Logo, para esse caso a solução da EDO é

i t = A e r 1 t + B e r 2 t

Substituindo os valores das raízes

i t = A e - 2 t + B e - 0,5 t

Passo 5

Encontramos uma expressão para a corrente do circuito, mas o que queremos determinar é a tensão no capacitor v 1 t para t > 0 . Sabemos que no capacitor

v 1 t = 1 C ∫ 0 t i   d t

Logo,

v 1 t = 1 0,25 ∫ 0 t A e - 2 t ' + B e - 0,5 t '   d t '

Resolvendo a integral por substituição simples, temos:

v 1 t = 4 A e - 2 t - 2 + B e - 0,5 t - 0,5

v 1 t = - 2 A e - 2 t - 8 B e - 0,5 t

Passo 6

Agora, precisamos encontrar os valores das constantes A e B . Como se trata de uma EDO de segunda ordem, precisamos da condição inicial da tensão v ( 0 + ) e de sua derivada d v ( 0 + ) / d t .

O enunciado nos disse que v 0 = 0 . Como no capacitor a tensão não varia instantaneamente:

v 1 0 + = 0

Portanto,

v 1 0 + = - 2 A e - 2 0 - 8 B e - 0,5 ( 0 )

- 2 A - 8 B = 0

Como o circuito é serie, a corrente é a mesma para todo o circuito e como no indutor a corrente não pode variar instantaneamente:

i 0 - = i 0 + = 2

Logo, no capacitor temos:

i 0 + = 0,25 d v 0 + d t

2 = 0,25 d v 0 + d t

d v 1 0 + d t = 8   V / s

Derivando v t ,   temos

d v 1 t d t = 4 A e - 2 t + 4 B e - 0,5 t

Então,

d v 1 0 + d t = 4 A e - 2 0 + 4 B e - 0,5 ( 0 )

4 A + 4 B = 8

Passo 7

Chegamos no seguinte sistema:

- 2 A - 8 B = 0   4 A + 4 B = 8

Multiplicando a primeira equação por dois e somando com a segunda, temos:

- 12 B = 8

B = - 8 12 = - 0,667

Logo,

A = - 8 - 0.667 2 = 2,667

Passo 8

Portanto, substituindo os valores das constantes, nossa solução final será:

v 1 t = - 2 ( 2,667 ) e - 2 t - 8 ( - 0,667 ) e - 0,5 t

v 1 t = - 5,33 e - 2 t + 5,33 e - 0,5 t     V

Como,

v t = - v 1 ( t )

v t = 5,33 e - 2 t - 5,33 e - 0,5 t     V

Resposta

v t = 5,33 e - 2 t - 5,33 e - 0,5 t     V

Exercício Resolvido #10

Livro Sadiku, p.322, Problema 8.24

A chave do circuito abaixo muda da posição A para B em t = 0 (observe atentamente que a chave tem de se conectar ao ponto B antes de ela desfazer a conexão em A , um interruptor). Determine i ( t ) para t > 0 .

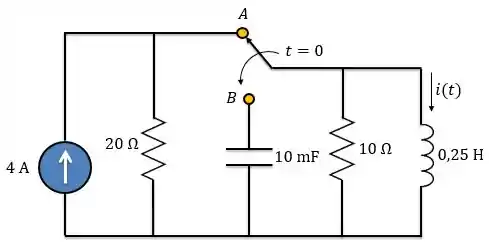
Passo 1

Vamos considerar que a chave estava na posição A por um longo tempo antes de t = 0 . Logo, o circuito já estava em seu regime permanente, ou seja, já podemos considerar o indutor funcionando como curto-circuito.

Passo 2

Logo, para instante exatamente antes da chave se abrir ( t = 0 - ) , a gente pode considerar o circuito assim:

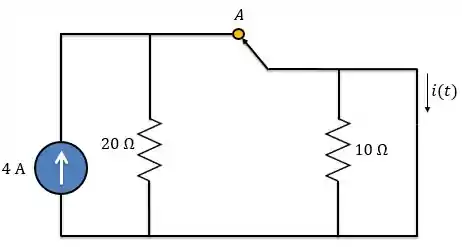
Como a corrente sempre escolhe o caminho mais fácil para ela circular, toda a corrente fornecida pela fonte de corrente passará pelo curto-circuito (indutor).

i 0 - = 4   A

Além disso, o capacitor está desconectado do circuito, logo não tem tensão em seus terminais.

v 0 - = 0

Passo 3

Agora, vamos analisar o circuito quando a chave muda para posição B . Em t = 0 + , podemos considerar o seguinte circuito:

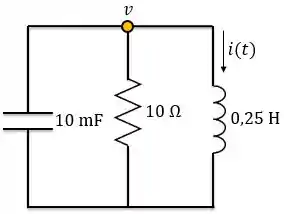
Esse circuito nós conhecemos bem. É o R L C paralelo sem fonte. Encontraremos a expressão da tensão nesse circuito utilizando α e ω 0 . Sabemos que para esse circuito

α = 1 2 R C               e             ω 0 = 1 L C

Passo 4

Substituindo os valores dos elementos do circuito, temos:

α = 1 2 10 0,01

α = 5

e

ω 0 = 1 0,25 0,01

ω 0 = 20

Passo 5

Como α < ω 0 , temos o caso de resposta subamortecida e vimos na teoria que sua solução é:

v t = e - α t ( A cos ⁡ ω d t + B sin ⁡ ω d t )

Sendo

ω d = ω 0 2 - α 2

ω d = ( 20 2 - 5 2 = 19,365

Substituindo esses valores, temos:

v t = e - 5 t ( A cos ⁡ 19,365 t + B sin ⁡ 19,365 t )

Passo 6

Encontramos uma expressão para a tensão do circuito, mas o que queremos determinar é a corrente no indutor i t para t > 0 . Sabemos que no indutor:

i t = 1 L ∫ 0 t v   d t

Logo,

i t = 1 0,25 ∫ 0 t e - 5 t ' ( A cos ⁡ 19,365 t ' + B sin ⁡ 19,365 t ' )   d t '

Mas não precisamos fazer essa integral, ainda bem né? Vou te explicar o porquê.

Como a nossa expressão para v ( t ) é formada por exponenciais, senos e cossenos, só as constantes sofrerão alterações e se tornarão em novas constantes. Logo, podemos dizer que a corrente i ( t ) será:

i t = e - 5 t ( D cos ⁡ 19,365 t + F sin ⁡ 19,365 t )

Onde D e F , são as novas constantes.

Passo 7

Agora, precisamos encontrar os valores das constantes D e F . Como se trata de uma EDO de segunda ordem, precisamos da condição inicial da corrente i ( 0 + ) e de sua primeira derivada d i ( 0 + ) / d t .

Nós calculamos i 0 - = 4 . Como no indutor a corrente não varia instantaneamente:

i 0 + = 4

Portanto,

i 0 + = e - 5 0 D cos ⁡ 19,365 0 + F sin ⁡ 19,365 0

Como, s i n ⁡ ( 0 ) = 0 e cos ⁡ 0 = 1 , temos:

i 0 + = D = 4

D = 4

Como o circuito é paralelo, a tensão v é a mesma para todo o circuito e como no capacitor a tensão não pode variar instantaneamente

v 0 - = v 0 + = 0

Logo, no indutor temos:

v 0 + = 0,25 d i 0 + d t

0 = 0,25 d i 0 + d t

d i 0 + d t = 0   A / s

Passo 8

Derivando i t ,   temos

d i t d t = d d t [ e - 5 t D cos ⁡ 19,365 t + F sin ⁡ 19,365 t )

Então, pela regra do produto:

d i t d t = - 5 e - 5 t ( D cos ⁡ 19,365 t + F sin ⁡ 19,365 t ) + e - 5 t ( - 19,365 D sin ⁡ 19,365 t + 19,365 F cos ⁡ 19,365 t )

Logo,

d i 0 + d t = - 5 D + 19,365 F = 0

Como D = 4 ,

- 5 ( 4 ) + 19,365 F = 0

F = 20 19,365

F = 1,033

Passo 9

Portanto, substituindo os valores das constantes, nossa solução final será

i t = e - 5 t ( 4 cos ⁡ 19,365 t + ( 1,033 ) sin ⁡ 19,365 t )

i t = e - 5 t ( 4 cos ⁡ 19,365 t + 1,033 sin ⁡ 19,365 t )   A

Resposta

i t = e - 5 t ( 4 cos ⁡ 19,365 t + 1,033 sin ⁡ 19,365 t )   A

Exercícios de Livros Relacionados

Um circuito RLC em paralelo possui L = 2 H e C = 0,25 F. O valor de R que produzirá um fator de amortecimento unitário é:(a) 0,5 Ω (b) 1 Ω (c) 2 Ω (d) 4 Ω
A equação que descreve a tensão em um circuito RLC é d 2 v d t 2 + 5 d v d t + 4 v = 0 Se v(0) = 0, dv(0)/dt = 10 V/s, obtenha v(t).
Sabe-se que a corrente no circuito da Figura P6.35 é io = 2e-5.000t(cos 1.000t + 5 sen 1.000t) Apara t $ 0+. Determine v1(0+) e v2(0+).
Para o circuito da Figura 8.58, a corrente inicial no indutor (em t = 0) é:(a) 0 A (b) 2 A (c) 6 A (d) 12 A
Obtenha v ( t ) para t0 no circuito da Figura 8.73.