Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Circuito RLC com fonte

Ver Todos os Exercícios

Teoria

Resposta ao degrau do circuito RLC série

Fala aí, beleza? No circuito abaixo queremos encontrar como resposta a tensão no capacitor v ( t ) . Como faríamos?

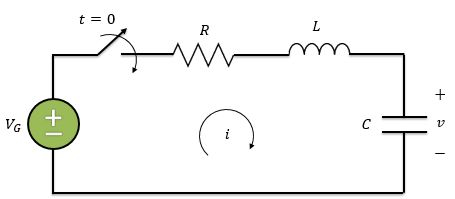
Em t = 0 a chave se fecha e é aplicado ao circuito subitamente a tensão V G . Lembrando que a resposta ao degrau é obtida por uma súbita aplicação de tensão ou corrente pela fonte, a gente pode entender o circuito acima também dessa maneira aqui:

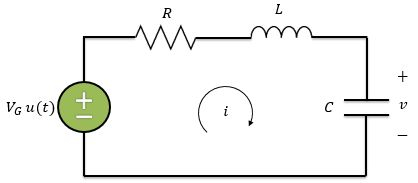
Onde u ( t ) é a função degrau unitário, que tem a seguinte a forma abaixo:

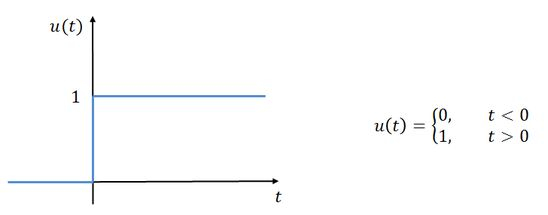
O que queremos, então, é encontrar a tensão no capacitor v ( t ) , sabendo que em t = 0 é aplicado subitamente um degrau de tensão no valor de V G . Para isso, vamos seguir esses passos:

1º PASSO:

Vamos aplicar a LTK no circuito, para t > 0 ,

R i + L d i d t + v = V G

Como, no capacitor

i = C d v d t

Substituindo i , temos

R C d v d t + L d C d v d t d t + v = V G

Arrumando essa bagunça,

L C d 2 v d t 2 + R C d v d t + v = V G

Dividindo todos os termos por L C ,

d 2 v d t 2 + R L d v d t + v L C = V G L C

2º PASSO:

Chegamos a uma EDO de segunda ordem não homogênea. A solução geral dessa equação é composta pela solução particular mais a solução da homogênea.

A solução da homogênea também é chamada de resposta natural do circuito, porque é como se a gente tivesse desligado a fonte V G = 0 . Já a solução particular da EDO é chamada de resposta forçada do circuito, porque é como se o circuito atingisse o regime permanente sofrendo a ação da fonte.

v t = v h ( t ) + v p ( t )

Primeiro, vamos resolver a homogênea:

d 2 v h d t 2 + R L d v h d t + v h L C = 0

Nós já resolvemos essa EDO quando estudamos o caso sem fontes no tópico anterior e vimos que dependendo do valor dos elementos temos três tipos de resposta:

Caso Superamortecido → α > ω 0 :

v h t = A e r 1 t + B e r 2 t

Caso de Amortecimento crítico → α = ω 0 :

v h t = ( A + B t ) e - α t

Caso Subamortecido → α < ω 0 :

v h t = e - α t ( A c o s   ω d t + B s i n   ω d t )

3º PASSO:

Agora, precisamos encontrar a solução particular.

d 2 v p d t 2 + R L d v p d t + v p L C = V G L C

Como V G / L C é uma constante, a solução particular deve ser também uma constante:

v p t = B ,

sendo B uma constante.

Substituindo, temos:

d 2 ( B ) d t 2 + R L d ( B ) d t + ( B ) L C = V G L C

Como a derivada de uma constante é zero:

B L C = V G L C

B = V G

v p t = V G

Também podemos encontrar v p analisando o circuito no regime permanente, ou seja, quando t → ∞ .

No regime permanente, o indutor pode ser considerado um curto-circuito e o capacitor um circuito aberto. Logo, o circuito pode ser considerado assim:

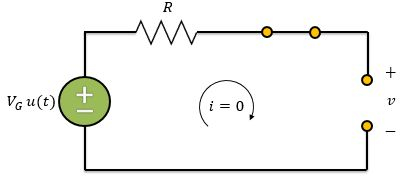
Portanto, como o circuito está aberto, a corrente é zero. Consequentemente, não há queda de tensão no resistor e a tensão v é a própria tensão da fonte.

Logo, a resposta forçada do circuito será

v p t = v ∞ = V G

4º PASSO:

Portanto, as soluções gerais para cada caso serão:

v t = V G + A e r 1 t + B e r 2 t     →     S u p e r a m o r t e c i d o

v t = V G + A + B t e - α t     →     A m o r t e c i m e n t o   c r í t i c o

v t = V G + e - α t A c o s   ω d t + B s i n   ω d t     →     S u b a m o r t e c i d o

Onde, no circuito R L C série

α = R 2 L   ,           ω 0 = 1 L C ,         ω d = ω 0 2 - α 2      

e as raízes da equação das características são

r 1,2 = - α ± α 2 - ω 0 2  

Lembrando que A e B são constantes que determinamos a partir das nossas condições iniciais: v ( 0 ) e d v ( 0 ) / d t .

Ficou confuso? Vamos fazer um exemplo numérico para clarear!

Vamos encontrar v ( t ) no circuito abaixo:

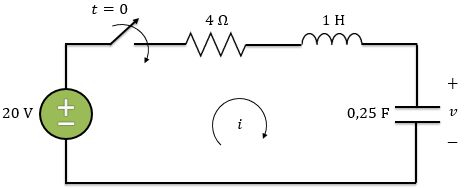
Acabamos de ver que para encontrarmos v ( t ) em um circuito R L C série com fonte, precisamos resolver a EDO de segunda ordem não homogênea. Além disso, a solução geral para v ( t ) possui duas parcelas.

v = v h + v p

A resposta natural depende de cada caso. Então, primeiro vamos ver qual o caso do nosso circuito.

Para t > 0 ,   a chave se fecha e em um circuito R L C série sabemos que

α = R 2 L               e               ω 0 = 1 L C

Logo, substituindo os valores:

α = 4 2 = 2

ω 0 = 1 1 × 0,25 = 2  

Como α = ω 0 , nossa resposta natural é criticamente amortecida e será:

v h t = A + B t e - α t

Substituindo o valor de α ,

v h t = A + B t e - 2 t

Agora, vamos encontrar a resposta forçada pela fonte de tensão. No regime permanente, o circuito pode ser considerado assim:

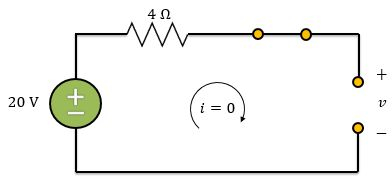
Logo,

v p = 20   V

Portanto, nossa solução completa é

v t = 20 + A + B t e - 2 t

Estamos quase acabando! Para terminar, precisamos encontrar o valor das constantes A e B . Para isso vamos precisar das nossas condições iniciais: v ( 0 + ) e d v ( 0 + ) / d t .

Para t < 0 , a fonte de tensão estava desligada e o capacitor e indutor sem energia armazenada. Logo,

v 0 - = 0

i 0 - = 0

Como no capacitor a tensão não pode variar instantaneamente,

v 0 - = v 0 + = 0

Portanto,

v 0 + = 20 + A + B 0 e - 2 0 = 0

20 + A = 0

A = - 20

Além disso, a corrente no indutor não pode variar instantaneamente e ela é a mesma do capacitor.

i 0 + = 0,25 d v 0 + d t = 0

d v 0 + d t = 0

Derivando v ( t ) em relação ao tempo, temos

d v d t = B e - 2 t + A + B t e - 2 t - 2

d v 0 + d t = B - 2 A = 0

B = - 40

Logo, a solução completa será

v t = 20 + - 20 - 40 t e - 2 t     V

Resposta ao degrau do circuito RLC paralelo

Agora, vamos estudar a resposta ao degrau no R L C paralelo. A gente vai ver que, para encontrar a resposta desse circuito, o procedimento é praticamente o mesmo que utilizamos no circuito série.

No circuito abaixo, queremos encontrar como resposta a corrente no indutor i ( t ) .

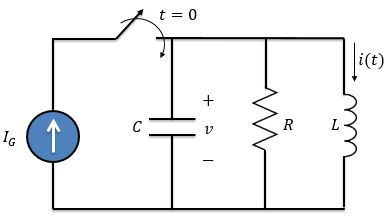
Vamos começar! Queremos encontrar a corrente no indutor i ( t ) , sabendo que em t = 0 é aplicado subitamente um degrau de corrente no valor de I G . Para isso, vamos seguir esses passos:

1º PASSO:

Vamos aplicar a LCK no circuito, para t > 0 ,

C d v d t + v R + i = I G

Como, no indutor

v = L d i d t

Substituindo v e dividindo todos os termos por L C , temos

d 2 i d t 2 + 1 R C d i d t + i L C = I G L C

2º PASSO:

Chegamos a mais uma EDO de segunda ordem não homogênea. A solução dela também é composta pela solução particular mais a solução da EDO homogênea associada.

i t = i h ( t ) + i p ( t )

Assim como no caso do circuito série, a solução da homogênea também é chamada de resposta natural do circuito e a solução particular da EDO é chamada de resposta forçada do circuito.

Primeiro, vamos encontrar a solução particular.

d 2 i p d t 2 + 1 R C d i p d t + i p L C = I G L C

Como I G / L C é uma constante, a solução particular deve ser também uma constante:

i p t = B ,

sendo B uma constante.

Substituindo, temos:

d 2 ( B ) d t 2 + 1 R C d ( B ) d t + ( B ) L C = I G L C

Como a derivada de uma constante é zero:

B L C = I G L C

B = I G

i p t = I G

Assim como no circuito série, também podemos encontrar i p analisando o circuito no regime permanente, ou seja, quando t → ∞ .

i p t = i ∞ = I G

3º PASSO:

Agora, vamos resolver a EDO homogênea:

d 2 i h d t 2 + 1 R C d i h d t + i h L C = 0

Essa EDO apesenta a mesma equação característica da EDO do circuito R L C paralelo sem fontes que vimos no tópico anterior. Logo, a resposta natural é a mesma que calculamos no caso sem fontes e vimos que, dependendo do valor dos elementos, temos três tipos de resposta.

4º PASSO:

Portanto, as soluções gerais para cada caso serão:

i t = I G + A e r 1 t + B e r 2 t     →     S u p e r a m o r t e c i d o

i t = I G + A + B t e - α t     →     A m o r t e c i m e n t o   c r í t i c o

i t = I G + e - α t A c o s   ω d t + B s i n   ω d t     →     S u b a m o r t e c i d o

Onde, no circuito R L C paralelo

α = 1 2 R C   ,             ω 0 = 1 L C   ,             ω d = ω 0 2 - α 2        

e

r 1,2 = - α ± α 2 - ω 0 2  

Sempre lembrando que A e B são constantes que determinamos a partir das nossas condições iniciais: i ( 0 ) e d i ( 0 ) / d t .

Generalização

Agora que você já está fera em circuitos R L C série e paralelo, podemos aplicar o que vimos até aqui a qualquer circuito de segunda ordem.

Seguindo esses quatro passos mágicos abaixo, podemos determinar a resposta x ( t ) ao degrau, que pode ser tensão ou corrente, para qualquer circuito de segunda ordem.

  1. Determinar as condições iniciais x 0 e d x ( 0 ) / d t e o valor final x ∞ ;
  2. Determinar a resposta natural do circuito x h t desligando as fontes independentes e aplicando a LCK ou LTK para obter a EDO de segunda ordem, pela qual calcularemos as raízes da equação característica;
  3. Calcular a resposta forçada do circuito através de

    4. x p ( t ) = x ( ∞ )

  4. A resposta final será a soma da resposta natural com a resposta forçada

x t = x h t + x p t

Tendo x t , determinar as constantes a partir das condições iniciais x 0 e d x ( 0 ) / d t .

Para você ver que eu não estou mentindo, vamos encontrar a tensão v ( t ) para t > 0 no circuito abaixo.

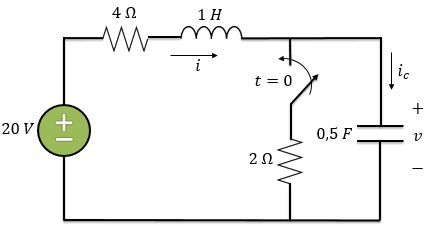
Como podemos ver, esse circuito não é um circuito R L C série nem paralelo, é um circuito de segunda ordem qualquer.

Vamos seguir nossos quatro passos.

1º PASSO:

Vamos determinar nossas condições iniciais e finais. Para t = 0 - , a chave está aberta e o circuito já atingiu o regime permanente. Então, podemos considerar o indutor um curto-circuito e o capacitor um circuito aberto.

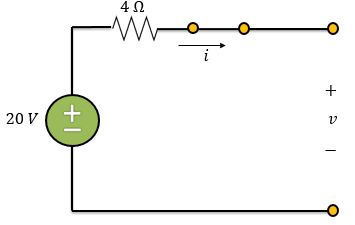
Como circuito está aberto, não há circulação de corrente e, consequentemente, não há queda de tensão no resistor. Logo,

v 0 - = 20   V

i 0 - = 0

Em t = 0 + , a chave é fechada.

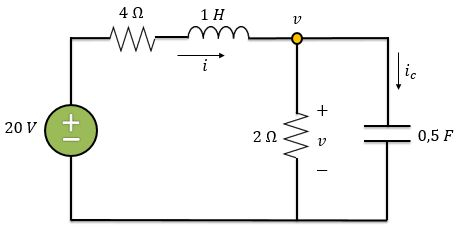
Como a tensão no capacitor não pode variar instantaneamente, assim como a corrente no indutor, temos que

v 0 + = v 0 - = 20   V

i 0 + = i 0 - = 0

Ainda precisamos determinar d v ( 0 + ) / d t . Sabemos que no capacitor

i c = C d v d t

Logo,

d v d t = i c 0,5

Aplicando LCK ao nó do circuito,

i 0 + = v 0 + 2 + i c ( 0 + )

0 = 20 2 + i c 0 +

i c 0 + = - 10   A

Portanto,

d v 0 + d t = - 20   V / s

Agora, precisamos encontrar o valor final. Isso ocorre quando t → ∞ e podemos considerar um novo regime permanente.

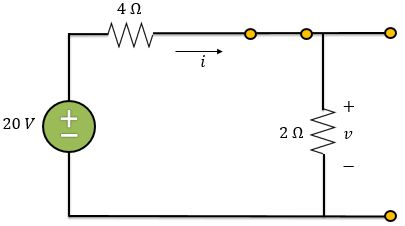
Aplicando divisor de tensão,

v ∞ = 2 4 + 2 × 20 = 6,667   V

2º PASSO:

Agora, vamos determinar a resposta natural para o circuito em t > 0 . Desligando a fonte de tensão, temos o circuito abaixo

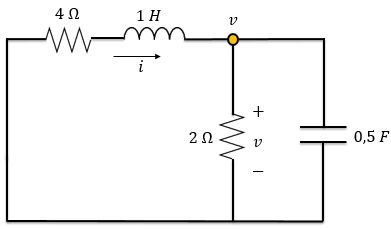
Lembrando que desligar a fonte de tensão é substituí-la por um curto-circuito.

Aplicando LCK ao nó do circuito acima,

i = v 2 + 1 2 d v d t

E aplicando LTK na malha da esquerda,

4 i + 1 d i d t + v = 0

Como a gente está querendo determinar a tensão v ( t ) , vamos substituir i da primeira equação na segunda.

2 v + 2 d v d t + 1 2 d v d t   + 1 2 d 2 v d t 2 + v = 0

Arrumando os termos,

d 2 v d t 2 + 5 d v d t + 6 v = 0

A equação característica para essa equação é

r 2 + 5 r + 6 = 0

Resolvendo a equação, chegamos as raízes

r 1 = - 2       e       r 2 = - 3

Logo, a resposta natural é

v t = A e - 2 t + B e - 3 t

3º PASSO:

Já determinamos o valor final da tensão. Logo a resposta forçada é

v p t = v ∞ = 6,667   V

4º PASSO:

Portanto, nossa solução completa é

v t = v h t + v p t

v t = 6,667 + A e - 2 t + B e - 3 t

Agora, precisamos determinar o valor de cada constante. Faremos isso, usando nossas condições iniciais.

v 0 + = 6,667 + A e - 2 0 + B e - 3 0 = 20

A + B = 13,333

Derivando v t , temos

d v d t = - 2 A e - 2 t - 3 B e - 3 t

Logo,

d v 0 + d t = - 2 A e - 2 0 - 3 B e - 3 0 = - 20

- 2 A - 3 B = - 20

Resolvendo o sistema abaixo,

A + B = 13,333 - 2 A - 3 B = - 20

Temos, A = 20 e B = - 6,667 .

Portanto, a solução completa é

v t = 6,667 + 20 e - 2 t - 6,667 e - 3 t     V

Resposta ao degrau do circuito RLC paralelo

Generalização

Exercícios Resolvidos

Exercício Resolvido #1

Livro Sadiku, p.322, Problema 8.26

A resposta a um degrau de um circuito R L C é descrita por

d 2 i d t 2 + 2 d i d t + 5 i = 10

Dado que i 0 = 2 e d i ( 0 ) / d t = 4 , determine i ( t ) .

Passo 1

O enunciado forneceu para a gente a expressão para a corrente e suas condições iniciais. Então, para encontrarmos i ( t ) precisamos resolver a EDO de segunda ordem não homogênea.

d 2 i d t 2 + 2 d i d t + 5 i = 10

Passo 2

A solução dessa EDO terá duas parcelas: uma referente à resposta natural e outra referente à resposta forçada.

i t = i h t + i p t

Primeiro, vamos encontrar a resposta natural, que é a solução da EDO homogênea associada a EDO do nosso circuito.

d 2 i h d t 2 + 2 d i h d t + 5 i h = 0

Passo 3

Essa EDO tem a seguinte equação característica,

r 2 + 2 r + 5 = 0

Vamos encontrar as raízes dessa equação.

r 1,2 = - 2 ± 2 2 - 20 2

r 1,2 = - 1 ± j 2

Passo 4

Encontramos raízes imaginárias. Para esse caso, a solução geral é:

i h t = e - α t ( A cos ⁡ ω d t + B sin ⁡ ω d t )

Onde,

r 1,2 = - α ± j ω d

Logo, para a nossa EDO

- α = - 1                 e                   ω d = 2

Então, nossa solução homogênea será:

i h t = e - t ( A cos ⁡ 2 t + B sin ⁡ 2 t )

Passo 5

Agora, vamos encontrar a solução particular, que é a resposta forçada do circuito.

d 2 i p d t 2 + 2 d i p d t + 5 i p = 10

Como 10 é uma constante, a solução particular deve ser também uma constante:

i p t = C ,

sendo C uma constante.

Substituindo, temos:

d 2 ( C ) d t 2 + 2 d ( C ) d t + 5 ( C ) = 10

Como a derivada de uma constante é zero:

5 C = 10

C = 2

Logo,

i p t = 2

Passo 6

Agora que encontramos a resposta natural e a forçada é só somar as duas.

i t = i h t + i p t

Portanto, a solução completa para a EDO de segunda ordem é

i t = e - t ( A cos ⁡ 2 t + B sin ⁡ 2 t ) + 2

Passo 7

Para terminar, precisamos encontrar o valor das constantes A e B . Para isso, vamos utilizar as condições iniciais.

i 0 = 2

e - 0 ( A cos ⁡ 2 0 + B sin ⁡ 2 ( 0 ) ) + 2 = 2

A + 2 = 2

A = 0

Para encontrarmos B , vamos derivar i ( t ) para usarmos a outra condição inicial. Já sabemos que A = 0 , então

i t = e - t ( B sin ⁡ 2 t ) + 2

Derivando,

d i d t = - e - t ( B sin ⁡ 2 t ) + e - t B ( 2 ) cos ⁡ 2 t

Logo,

d i 0 d t = 2 B

Como o enunciado nos disse que

d i 0 d t = 4

Temos,

2 B = 4

B = 2

Passo 8

Portanto, substituindo os valores encontrados para as constantes, a solução completa para a EDO de segunda ordem é

i t = e - t ( ( 0 ) cos ⁡ 2 t + ( 2 ) sin ⁡ 2 t ) + 2

i t = 2 e - t sin ⁡ 2 t + 2       A

Resposta

i t = 2 e - t sin ⁡ 2 t + 2       A

Exercício Resolvido #2

Livro Sadiku, p.322, Problema 8.27

Uma tensão de ramo em um circuito R L C é descrita por

d 2 v d t 2 + 4 d v d t + 8 v = 24

Se as condições iniciais forem v 0 = 0 = d v ( 0 ) / d t , determine v ( t ) .

Passo 1

O enunciado forneceu para a gente qual a expressão para a tensão e suas condições iniciais. Então, para encontrarmos v ( t ) precisamos resolver a EDO de segunda ordem não homogênea.

d 2 v d t 2 + 4 d v d t + 8 v = 24

Passo 2

A solução dessa EDO terá duas parcelas: uma referente à resposta natural e outra referente à resposta forçada.

v t = v h t + v p t

Primeiro, vamos encontrar a resposta natural, que é a solução da EDO homogênea associada a EDO do nosso circuito.

d 2 v h d t 2 + 4 d i h d t + 8 v h = 0

Passo 3

Essa EDO tem a seguinte equação característica,

r 2 + 4 r + 8 = 0

Vamos encontrar as raízes dessa equação.

r 1,2 = - 4 ± 4 2 - 32 2

r 1,2 = - 2 ± j 2

Passo 4

Encontramos raízes imaginárias. Para esse caso, a solução geral é

v h t = e - α t ( A cos ⁡ ω d t + B sin ⁡ ω d t )

Onde,

r 1,2 = - α ± j ω d

Logo, para a nossa EDO

- α = - 2               e                   ω d = 2

Então, nossa solução homogênea será

v h t = e - 2 t ( A cos ⁡ 2 t + B sin ⁡ 2 t )

Passo 5

Agora, vamos encontrar a solução particular, que é a resposta forçada do circuito.

d 2 v p d t 2 + 4 d v p d t + 8 v p = 24

Como 24 é uma constante, a solução particular deve ser também uma constante:

v p t = C ,

sendo B uma constante.

Substituindo, temos:

d 2 ( C ) d t 2 + 4 d ( C ) d t + 8 ( C ) = 24

Como a derivada de uma constante é zero:

8 C = 24

C = 3

Logo,

v p t = 3

Passo 6

Agora que encontramos a resposta natural e a forçada é só somar as duas.

v t = v h t + v p t

Portanto, a solução completa para a EDO de segunda ordem é

v t = e - 2 t ( A cos ⁡ 2 t + B sin ⁡ 2 t ) + 3

Passo 7

Para terminar, precisamos encontrar o valor das constantes A e B . Para isso, vamos utilizar as condições iniciais.

v 0 = 0

e - 2 0 ( A cos ⁡ 2 0 + B sin ⁡ 2 ( 0 ) ) + 3 = 0

A + 3 = 0

A = - 3

Para encontrarmos B , vamos derivar v ( t ) para usarmos a outra condição inicial. Já sabemos que A = - 3 , então

v t = e - 2 t ( - 3 cos ⁡ 2 t + B sin ⁡ 2 t ) + 3

Derivando,

d v d t = - 2 e - 2 t ( - 3 cos ⁡ 2 t + B sin ⁡ 2 t ) + e - 2 t ( 3 ( 2 ) sin ⁡ 2 t + B ( 2 ) cos ⁡ 2 t )

Logo,

d v 0 d t = 6 + 2 B

Como o enunciado nos disse que

d v 0 d t = 0

Temos,

6 + 2 B = 0

B = - 3

Passo 8

Portanto, substituindo os valores encontrados para as constantes, a solução completa para a EDO de segunda ordem é

v t = e - 2 t ( - 3 cos ⁡ 2 t - 3 sin ⁡ 2 t ) + 3

v t = - 3 e - 2 t ( cos ⁡ 2 t + sin ⁡ 2 t ) + 3       V

Resposta

v t = - 3 e - 2 t ( cos ⁡ 2 t + sin ⁡ 2 t ) + 3       V

Exercício Resolvido #3

Livro Sadiku, p.324, Problema 8.53

Após estar aberta por um dia, a chave do circuito abaixo é fechada em t = 0 . Determine a equação diferencial que descreve i t ,   t > 0 .

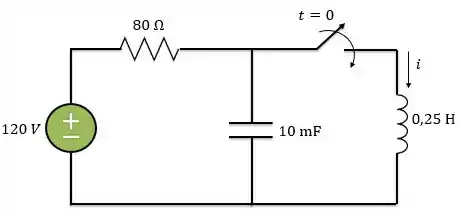
Passo 1

Nesse exercício não precisamos encontrar como se comporta a corrente para t > 0 . Precisamos encontrar a EDO de segunda ordem que descreve essa corrente.

Nós vimos que é possível encontrar i ( t ) sem precisarmos encontrar a EDO antes. Mas na realidade, como vimos na teoria, tudo parte de uma EDO de segunda ordem não homogênea. A partir dela chegamos nos casos de amortecimento e nas soluções gerais.

Passo 2

Para começar, vamos aplicar a LCK ao nó do circuito abaixo.

i 1 = i c + i

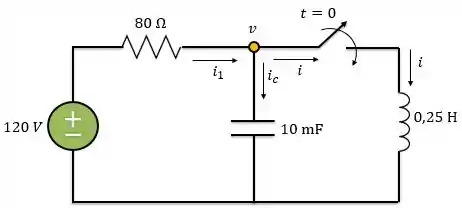
Pela lei de Ohm,

i 1 = 120 - v 80

i c = 0,01 d v d t

Substituindo,

120 - v 80 = 0,01 d v d t + i

Arrumando a equação, temos

120 - v = 0,8 d v d t + 80 i

120 = v + 0,8 d v d t + 80 i     ( 1 )

Passo 3

Como o indutor está em paralelo com o capacitor, eles possuem a mesma tensão v . Portanto, no indutor

v = 0,25 d i d t     ( 2 )

Como queremos encontrar uma EDO para a corrente, vamos substituir a equação ( 2 ) em ( 1 ) .

120 = 0,25 d i d t + 0,8 0,25 d 2 i d t 2 + 80 i

Arrumando a EDO,

0,2 d 2 i d t 2 + 0,25 d i d t + 80 i = 120

Para terminar, dividindo todos os termos por 0,2 ,

d 2 i d t 2 + 1,25 d i d t + 400 i = 600

Resposta

d 2 i d t 2 + 1,25 d i d t + 400 i = 600

Exercício Resolvido #4

Introdução a análise de circuitos - Robert L Boylestad – Ed. 12 – Exercício 11.43

Determine as correntes de estado estacionário I 1 e I 2 para o circuito na figura:

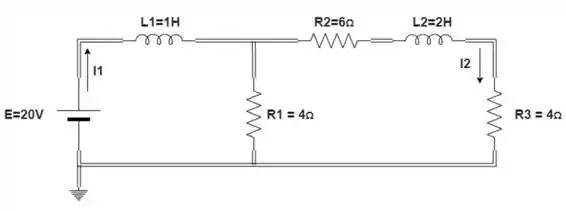
Passo 1

Substituir o indutor L 1 por um curto-circuito, por onde passa a corrente I 1 e substituir o indutor L 2 por um curto circuito por onde passa a corrente I 2 .

Passo 2

Assim temos um circuito simples, onde R 2 está em série com o resistor R 3 e estão em paralelo com o resistor R 1 .

Vamos calcular a resistência equivalente do circuito para calcular a corrente total que sai da fonte I 1 .

R 4 =   R 2 + R 3 = 6 + 4 = 10 Ω

R e q = 4 * 10 4 + 10 = 2,86 Ω

Passo 3

A corrente total I 1 é dada por:

I 1 = E R e q = 20 2,86 = 6,99 A

Passo 4

A corrente total I 2 é calculada através do divisor de corrente entre os ramos do circuito:

I 2 = I 1 * 4 10 + 4 =   6,99 * 4 14 = 2 A

Resposta

I 1 =   6,99 A

I 2 =   2 A

Exercício Resolvido #5

Introdução a análise de circuitos - Robert L Boylestad – Ed. 12 – Exercício 11.45

Determine as correntes e as tensões de estado estacionário para o circuito na figura após a chave ser fechada.

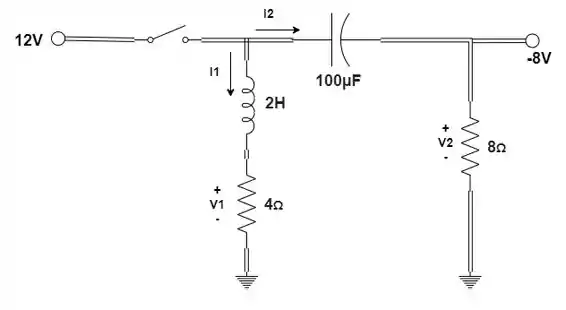
Passo 1

Após a chave ser fechada e o circuito entrar em estado estacionário, podemos substituir os indutores por um curto circuito e o capacitor por um circuito aberto.

Passo 2

Logo a corrente não circula pelo capacitor e assim

I 2 = 0 A

Passo 3

O circuito se torna apenas a fonte de 12 V em série com o resistor de 4 Ω . Assim a corrente se resume a:

I 1 = 12 4 = 3 A

Passo 4

A tensão V 1 é calculada pela multiplicação do resistor pela corrente que circula por ele:

V 1 = 4 * 3 = 12 V

Passo 5

Por outro lado, o resistor 8 Ω está em paralelo com a fonte de tensão de - 8 V , logo possui a mesma tensão da fonte:

V 2 =   - 8 V

Resposta

I 1 = 3 A

I 2 = 0 A

V 1 = 12 V

V 1 = - 8 V

Exercício Resolvido #6

Introdução a análise de circuitos - Robert L Boylestad – Ed. 12 – Exercício 11.41 Adaptada

Considerando o circuito na figura:

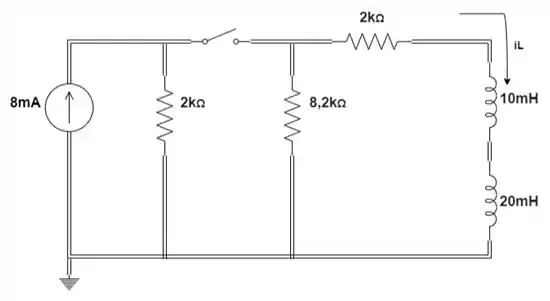
  1. Escreva a expressão matemática para a corrente i L se a chave for fechada em t = 0s.

Passo 1

Primeiro vamos converter a fonte de corrente em paralelo com o resistor em uma fonte de tensão em série com o resistor:

E = 8 m * 2 k = 16 V

Passo 2

Depois vamos converter a associação dos dois indutores em série:

L e q =   L 1 + L 2 = 10 m + 20 m = 30 m H

Passo 3

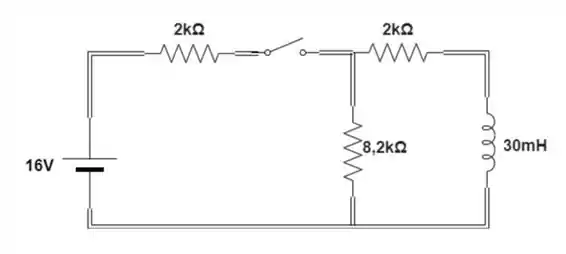
Passo 4

Após a chave fechar devemos calaular o equivalente Thévenin entre os terminais do indutor equivalente.

Primeiro a resistência equivalente ao substituir a fonte de tensão por um curto circuito:

R t h = 2 k * 8,2 k 2 k + 8,2 k + 2 k = 3,6 1 k Ω

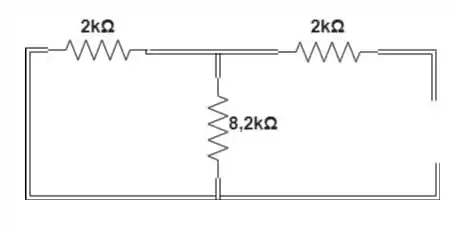
Passo 5

Calcular a tensão Thévenin entre os terminais do indutor:

E t h = 8,2 k 8,2 k + 2 k * 16 = 12,86 V

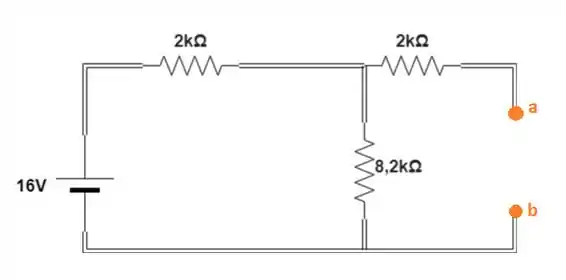
Passo 6

Agora podemos calcular a constante de tempo de carregamento do circuito τ :

τ =   L R =   30 m 3,61 k = 8,31 μ s

Passo 7

A corrente segue a seguinte fórmula para o carregamento:

i L =   E R ( 1 - e - t τ )

i L =   12,86 3,61 k ( 1 - e - t 8,31 μ )

i L =   3,56 ( 1 - e - t 8,31 μ ) m A

Resposta

i L =   3,56 ( 1 - e - t 8,31 μ ) m A

Exercício Resolvido #7

Livro Sadiku, p.324, Problema 8.45

No circuito abaixo, determine v t e i ( t ) para t > 0 . Suponha v 0 = 0   V e i 0 = 1   A .

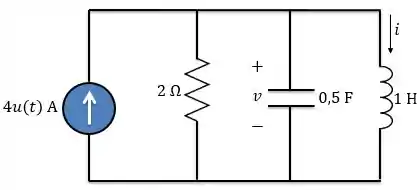
Passo 1

Esse é um circuito R L C paralelo clássico. O enunciado já nos deu de bandeja duas condições iniciais. Primeiro vamos determinar a corrente i ( t ) . Então, precisamos encontrar a condição inicial da derivada da corrente.

Passo 2

Como o circuito é paralelo, a tensão é a mesma para todos os elementos. Logo, no indutor

v = L d i d t

Em t = 0 + , como a tensão no capacitor não pode variar instantaneamente,

v 0 + = v 0 - = 0

Portanto,

v 0 + = 1 d i ( 0 + ) d t = 0

d i 0 + d t = 0

Passo 3

Agora que encontramos as condições iniciais, vamos encontrar os parâmetros α e ω 0 , para sabermos qual o tipo de amortecimento do circuito.

Sabemos que no circuito R L C paralelo

α = 1 2 R C = 1 2 2 0,5 = 0,5

ω 0 = 1 L C = 1 0,5 = 2

Como α < ω 0 , temos o caso de subamortecimento. Onde sua solução geral é

i t = I G + e - α t A c o s   ω d t + B s i n   ω d t

Onde, I G é a corrente da fonte e ω d = ω 0 2 - α 2 .

I G = 4   A

ω d = 2 - 0,25 = 1,323

Então, para esse circuito a corrente tem a seguinte expressão:

i t = 4 + e - 0,5 t A   c o s   1,323 t + B s i n   1,323 t

Passo 4

Agora, precisamos determinar o valor de cada constante. Faremos isso, usando nossas condições iniciais.

i t = 4 + e - 0,5 t A c o s   1,323 0 + B s i n   1,323 ( 0 ) = 1

4 + A = 1

A = - 3

Derivando i t , temos

d i d t = - 0,5 e - 0,5 t A c o s   1,323 t + B s i n   1,323 t + e - 0,5 t 1,323 ( - A sin ⁡ 1,323 t + B cos ⁡ 1,323 t )  

Logo,

d i 0 + d t - 0,5 A + 1,323 B = 0

B = 0,5 - 3 1,323 = - 1,134

Portanto, substituindo os valores das constantes, a solução completa final é

i t = 4 + e - 0,5 t - 3 c o s   1,323 t - 1,134 s i n   1,323 t     A

Passo 5

Agora que já encontramos a corrente que passa pelo indutor, vamos encontrar a tensão v ( t ) .

A gente já sabe que v ( t ) é a mesma para todos os elementos do circuito.

Como no indutor,

v = L d i d t

Basta derivarmos a corrente i ( t ) e multiplicá-la pelo valor do indutor. Nós acabamos de derivar a corrente no passo anterior e vimos que:

d i d t = - 0,5 e - 0,5 t A c o s   1,323 t + B s i n   1,323 t + e - 0,5 t 1,323 ( - A sin ⁡ 1,323 t + B cos ⁡ 1,323 t )

Substituindo o valor de cada constante:

d i d t = - 0,5 e - 0,5 t - 3 c o s   1,323 t - 1,134 s i n   1,323 t + e - 0,5 t 1,323 ( 3 sin ⁡ 1,323 t - 1,134 cos ⁡ 1,323 t )

d i d t = 1,5 e - 0,5 t c o s   1,323 t + 0,567 e - 0,5 t s i n   1,323 t + ( 3,969 e - 0,5 t sin ⁡ 1,323 t - 1,5 e - 0,5 t cos ⁡ 1,323 t )

d i ( t ) d t = 4,536 e - 0,5 t sin ⁡ 1,323 t

Como, L = 1   H

v t = d i ( t ) d t = 4,536 e - 0,5 t sin ⁡ 1,323 t     V

Resposta

i t = 4 + e - 0,5 t - 3 c o s   1,323 t - 1,134 s i n   1,323 t     A

v t = 4,536 e - 0,5 t sin ⁡ 1,323 t     V

Exercício Resolvido #8

Livro Sadiku, p.322, Problema 8.33

Determine v t para t > 0 no circuito abaixo.

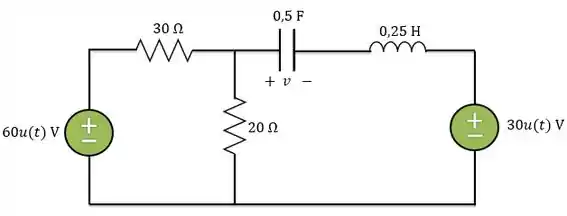
Passo 1

Como a gente pode ver, esse circuito não é um circuito R L C série nem paralelo, é um circuito de segunda ordem qualquer. Antes de mais nada, vamos determinar nossas condições iniciais e finais para a tensão v .

Para t = 0 - , as fontes de tensão valem zero, já que para t < 0 ,   u t = 0 . Ou seja, podemos considerar que não há energia armazenada no circuito.

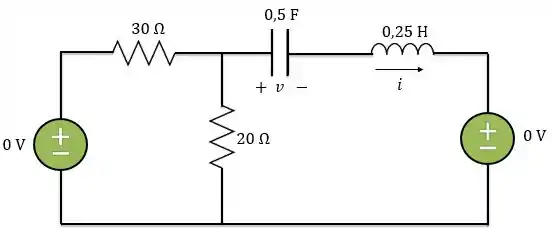
Logo,

v 0 - = 0

i 0 - = 0

Passo 2

Como a tensão no capacitor não pode variar instantaneamente, assim como a corrente no indutor, temos que

v 0 + = v 0 - = 0

i 0 + = i 0 - = 0

Ainda precisamos determinar d v ( 0 + ) / d t . Sabemos que no capacitor

i c = C d v d t

Como o capacitor e o indutor estão em série, a corrente neles é a mesma. Logo,

i c 0 + = i 0 + = 0

Portanto,

d v 0 + d t = i 0 + 0,5

d v 0 + d t = 0 0,5 = 0

Passo 3

Agora, precisamos encontrar o valor final da tensão no capacitor. Isso ocorre quando t → ∞ e podemos considerar que o circuito atingiu o regime permanente, no qual o indutor pode ser considerado um curto-circuito e o capacitor um circuito-aberto.

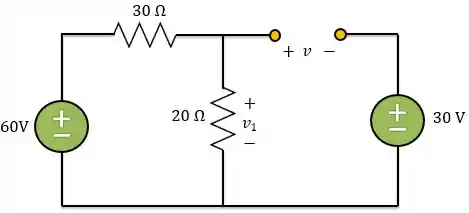
Aplicando LTK, na malha da direita, temos

- v 1 ∞ + v ∞ + 30 = 0

v ∞ = v 1 ∞ - 30

Aplicando divisor de tensão, encontramos a tensão v 1 :

v 1 ∞ = 20 20 + 30 × 60

v 1 ( ∞ ) = 24   V

Logo, o valor final da tensão no capacitor é:

v ∞ = 24 - 30 = - 6   V

Esse valor final é a resposta forçada do circuito,

v p t = v ∞ = - 6   V

Passo 4

Pronto, encontramos todas os nossos valores iniciais e a resposta forçada. Agora, vamos encontrar a resposta natural v h ( t ) para t > 0 . Para isso, precisamos desligar todas as fontes independentes do circuito.

Lembrando que desligar uma fonte de tensão é o mesmo que considerá-la um curto-circuito. Logo, teremos o circuito abaixo:

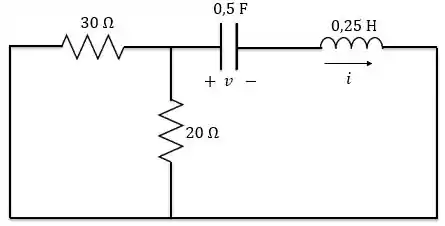
Fazendo a associação dos resistores em paralelo, temos

R e q = 20   ×   30 20 + 30 = 12   Ω

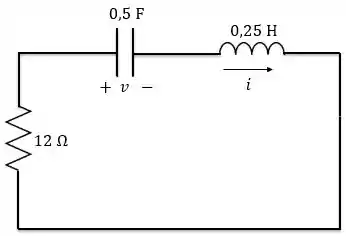
Olha que maravilha! Chegamos ao circuito R L C série sem fontes e nele sabemos que:

α = R 2 L = 12 0,5 = 24

ω 0 = 1 L C = 1 ( 0,25 ) ( 0,5 ) = 2,828

Como α > ω 0 , temos o caso superamortecido. Esse caso tem a seguinte solução geral:

v h t = A e r 1 t + B e r 2 t

Onde as raízes são,

r 1,2 = - α ± α 2 - ω 0 2

Substituindo os valores de α e ω 0 , temos

r 1,2 = - 24 ± 24 2 - 2,838 2

Logo,

r 1 = - 0,168

r 2 = - 47,83

Portanto, nossa resposta natural é

v h t = A e - 0,168 t + B e - 47,83 t

Passo 5

A solução completa é a soma da resposta natural com a resposta forçada.

v t = v h t + v p t

v t = A e - 0,168 t + B e - 47,83 t - 6

Agora, precisamos determinar o valor de cada constante. Faremos isso, usando nossas condições iniciais.

v 0 + = A e - 0,168 0 + B e - 47,83 0 - 6 = 0

A + B = 6

Derivando v t , temos

d v d t = - 0,168 A e - 0,168 t - 47,83 B e - 47,83 t

Logo,

d v 0 + d t = - 0,168 A e - 0,168 ( 0 ) - 47,83 B e - 47,83 ( 0 ) = 0

- 0,168 A - 47,83 B = 0

Resolvendo o sistema abaixo,

A + B = 6 - 0,168 A - 47,83 B = 0

Isolando A na primeira equação e substituindo na segunda, temos

- 0,168 6 - B - 47,83 B = 0

- 1,008 + 0,168 B - 47,83 B = 0

- 47,66 = 1,008

B = - 0,021

Logo,

A = 6 - ( - 0,021 ) = 6,021

Portanto, a solução completa final é:

v t = 6,021 e - 0,168 t - 0,021 e - 47,83 t - 6       V

Resposta

v t = 6,021 e - 0,168 t - 0,021 e - 47,83 t - 6       V

Exercício Resolvido #9

Livro Sadiku, p.322, Problema 8.33

Determine v t para t > 0 no circuito abaixo.

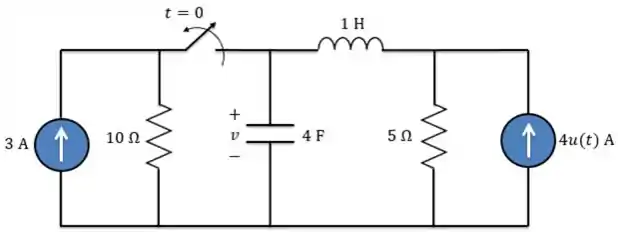
Passo 1

Antes de mais nada, vamos determinar nossas condições iniciais e finais para a tensão v .

Para t = 0 - , a chave está fechada e o circuito já atingiu o regime permanente. Então, podemos considerar o indutor um curto-circuito e o capacitor um circuito aberto.

Além disso, a fonte de corrente da esquerda vale zero, já que para t < 0 ,   u t = 0 . Ou seja, podemos considerá-la desligada.

Passo 2

Então, para t = 0 - , analisamos o circuito abaixo.

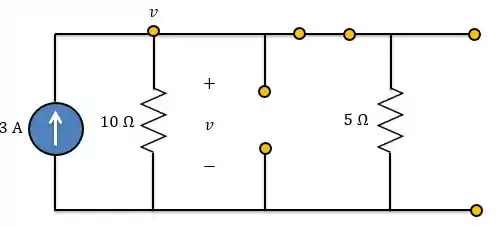
Redesenhando

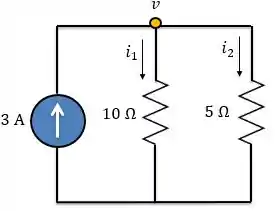
Aplicando LCK ao nó,

3 = i 1 + i 2

3 = v ( 0 - ) 10 + v ( 0 - ) 5

3 v 0 - = 30

v 0 - = 10   V

Se repararmos, i 2 é a corrente que passa pelo indutor e seu valor será

i 2 0 - = 10 5 = 2   A

Passo 3

Precisamos encontrar a condição inicial para a derivada da tensão. Em t = 0 + , a chave é aberta e temos o seguinte circuito.

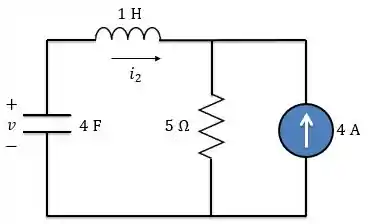
Agora vamos fazer uma coisa que vai facilitar muito: usar transformação de fontes. A fonte de corrente que está em paralelo com o resistor vai se transformar numa fonte de tensão em série com o resistor. Lembra disso?

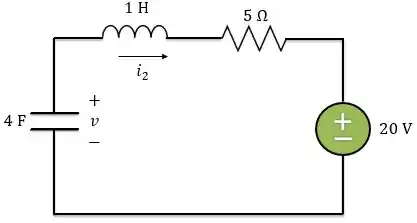
O circuito acima nós conhecemos bem! É o circuito R L C série.

Lembrando que a fonte de tensão tem valor de 20   V , porque quando realizamos a transformação de fontes temos que respeitar a lei de Ohm

V = 5 × 4 = 20   V

Passo 4

Como a tensão no capacitor não pode variar instantaneamente, assim como a corrente no indutor, temos que

v 0 + = v 0 - = 10   V

i 2 0 + = i 2 0 - = 2   A

Ainda precisamos determinar d v ( 0 + ) / d t . Sabemos que no capacitor

i c = C d v d t

Como o circuito é série, a corrente em todos os elementos é a mesma. Logo,

i c 0 + = i 2 0 + = 2   A

Temos que tomar cuidado agora. Veja que a corrente i 2 está no sentido contrário a convenção de sinais em elementos passivos no capacitor. Logo,

i 2 = - C d v d t

Portanto,

d v 0 + d t = - i 2 0 + 4  

d v 0 + d t = - 2 4 = - 0,5   V / s

Passo 5

Agora, precisamos encontrar o valor final. Isso ocorre quando t → ∞ e podemos considerar um novo regime permanente, no qual mais uma vez o indutor pode ser considerado um curto-circuito e o capacitor um circuito-aberto.

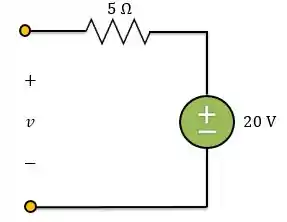
Como o circuito está aberto, não há circulação de corrente e, consequentemente, queda de tensão no resistor. Portanto, a tensão v será a própria tensão da fonte.

v ∞ = 20   V

Passo 6

Pronto, encontramos todas os nossos valores iniciais e finais. Agora, vamos encontrar a expressão para v ( t ) para t > 0 .

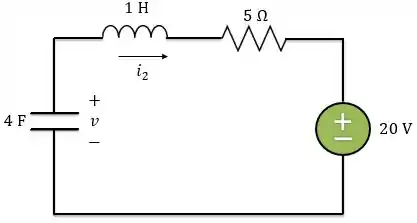
Como o circuito é R L C série sabemos que

α = R 2 L = 5 2 = 2,5

ω 0 = 1 L C = 1 4 = 0,5

Como α > ω 0 , temos o caso superamortecido. Esse caso tem a seguinte solução geral.

v t = v ( ∞ ) + A e r 1 t + B e r 2 t

Onde as raízes são,

r 1,2 = - α ± α 2 - ω 0 2

Substituindo os valores de α e ω 0 , temos

r 1,2 = - 2,5 ± 2,5 2 - 0 , 5 2

Logo,

r 1 = - 0,0505

r 2 = - 4,949

Portanto, nossa solução completa é

v t = 20 + A e - 0,0505 t + B e - 4,949 t

Passo 7

Agora, precisamos determinar o valor de cada constante. Faremos isso, usando nossas condições iniciais.

v 0 + = 20 + A e - 0,0505 ( 0 ) + B e - 4,949 ( 0 ) = 10

A + B = - 10

Derivando v t , temos

d v d t = - 0,0505 A e - 0,0505 t - 4,949 B e - 4,949 t

Logo,

d v 0 + d t = - 0,0505 A e - 0,0505 ( 0 ) - 4,949 B e - 4,949 ( 0 ) = - 0,5

- 0,0505 A - 4,949 B = - 0,5

Resolvendo o sistema abaixo,

A + B = - 10 - 0,0505 A - 4,949 B = - 0,5

Isolando A na primeira equação e substituindo na segunda, temos

- 0,0505 - 10 - B - 4,949 B = - 0,5

0,505 + 0,0505 B - 4,949 B = - 0,5

- 4,8985 B = - 1,005

B = 0,205

Logo,

A = - 10 - 0,205 = - 10,205

Portanto, a solução completa final é

v t = 20 - 10,205 e - 0,0505 t + 0,205 e - 4,949 t     V

Resposta

v t = 20 - 10,205 e - 0,0505 t + 0,205 e - 4,949 t     V

Exercício Resolvido #10

Livro Sadiku, p.324, Problema 8.50

Para o circuito abaixo, determine i ( t ) para t > 0 .

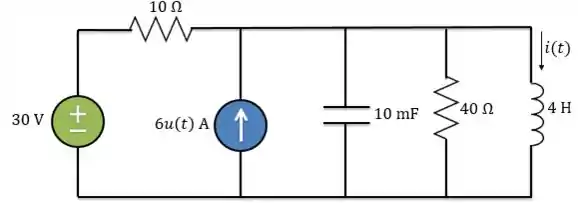
Passo 1

Antes de mais nada, vamos determinar nossas condições iniciais e finais para a corrente i .

Em t = 0 - , o circuito já atingiu o regime permanente. Então, podemos considerar o indutor um curto-circuito e o capacitor um circuito aberto.

Além disso, a fonte de corrente vale zero, já que para t < 0 ,   u t = 0 . Ou seja, podemos considerá-la desligada.

Passo 2

Então, para t = 0 - , analisamos o circuito abaixo.

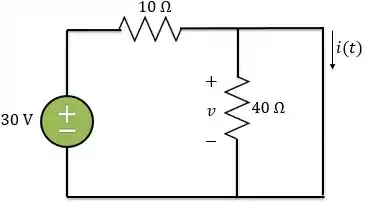
A corrente fornecida pela fonte passará toda pelo curto circuito. Logo, não passará corrente pelo resistor de 40   Ω . Logo, pela lei de Ohm,

i 0 - = 30 10 = 3   A

v 0 - = 0

Passo 3

Precisamos encontrar a condição inicial para a derivada da corrente. Em t = 0 + , a fonte de corrente passa a funcionar e vale 6   A . Então, a gente tem esse circuito aí.

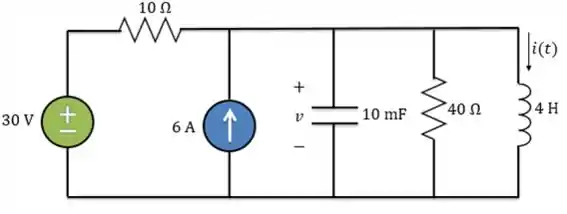
Como a tensão no capacitor não pode variar instantaneamente, assim como a corrente no indutor, temos que

v 0 + = v 0 - = 0   V

i 0 + = i 0 - = 3   A

Como o circuito é paralelo, a tensão é a mesma para todos os elementos. Logo, no indutor

v = L d i d t

Em t = 0 + , como a tensão no capacitor não pode variar instantaneamente,

v 0 + = v 0 - = 0

Portanto,

v 0 + = 4 d i ( 0 + ) d t = 0

d i 0 + d t = 0

Passo 4

Agora, nós vamos fazer uma coisa que vai nos facilitar muito. Vamos usar transformação de fontes. A fonte de tensão que está em série com o resistor vai se transformar numa fonte de corrente em paralelo com o resistor. Lembra disso?

Quando realizamos a transformação de fontes temos que respeitar a lei de Ohm. Logo o valor da fonte de corrente será

I = V R = 30 10 = 3   A

Logo, nosso circuito ficará assim,

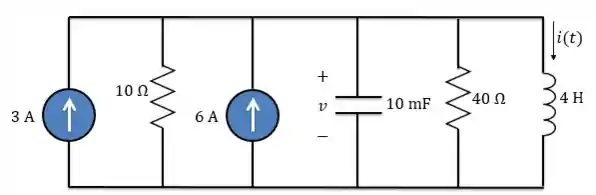
Ainda podemos reduzir mais o circuito, já que temos dois resistores em paralelo e duas fontes de corrente também em paralelo.

Então, somando o valor das fontes e calculando a resistência equivalente

R e q = 10 × 40 10 + 40 = 8   Ω

Chegamos ao circuito abaixo.

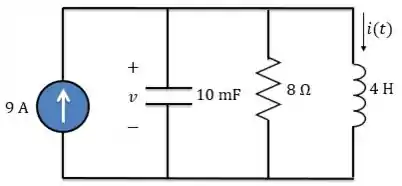
Esse circuito nós conhecemos bem! É o circuito R L C Paralelo.

Passo 5

Agora, vamos encontrar os parâmetros α e ω 0 , para sabermos qual o tipo de amortecimento do circuito.

Sabemos que no circuito R L C paralelo

α = 1 2 R C = 1 2 8 0,01 = 6,25

ω 0 = 1 L C = 1 ( 4 ) ( 0,01 ) = 5

Como α > ω 0 , temos o caso de superamortecimento. Onde sua solução geral é

i t = I G + A e r 1 t + B e r 2 t

Onde, I G é a corrente da fonte e

r 1,2 = - α ± α 2 - ω 0 2

Portanto,

I G = 9   A

r 1 = - 6,25 + 6,25 2 - 5 2

r 1 = - 6,25 + 3,75 = - 2,5

e

r 2 = - 6,25 - 3,75 = - 10

Então, para esse circuito a corrente tem a seguinte expressão

i t = 9 + A e - 2,5 t + B e - 10 t

Passo 6

Agora, precisamos determinar o valor de cada constante. Faremos isso, usando nossas condições iniciais.

i 0 + = 3   A                 e                 d i 0 + d t = 0

Logo,

i 0 + = 9 + A e - 2,5 ( 0 ) + B e - 10 ( 0 ) = 3

9 + A + B = 3

A + B = - 6

Derivando i t , temos

d i d t = - 2,5 A e - 2,5 t - 10 B e - 10 t

Logo,

d i 0 + d t = - 2,5 A e - 2,5 ( 0 ) - 10 B e - 10 ( 0 ) = 0

- 2,5 A - 10 B = 0

Resolvendo o sistema abaixo,

A + B = - 6 - 2,5 A - 10 B = 0

Isolando A na primeira equação e substituindo na segunda, temos

- 2,5 - 6 - B - 10 B = 0

15 + 2,5 B - 10 B = 0

- 7,5 B = - 15

B = 2

Logo,

A = - 6 - 2 = - 8

Portanto, a solução completa final é

i t = 9 - 8 e - 2,5 t + 2 e - 10 t         A

Resposta

i t = 9 - 8 e - 2,5 t + 2 e - 10 t         A

Exercícios de Livros Relacionados

Para o circuito da Figura 8.65, determine:(a) v 0 +ei ( 0 + ) (b) d v ( 0 + ) / d ted i ( 0 + ) / d t (c) v ∞ei ( ∞ )
Calcule v para t0 , se o circuito está em regime permanente em t = 0 - ,
Referindo-se ao circuito da Figura 8.66, determine:(a) i ( 0 + ) e v ( 0 + ) (b) d i ( 0 + ) / d t e d v ( 0 + ) / d t (c) i ( ∞ ) e v ( ∞ )
Usando a Figura 8.9 3 , elabore um problema para ajudar outros estudantes a entenderem melhor a resposta a um degrau de um circuito R L C em paralelo.
Obtenha v(t) e i(t) para t0 no circuito da Figura 8.84.