Circuito com Transformadores no Modelo Série
Produzido por Alexandre NunesTeoria
Agora que estamos feras em sistema PU e sabemos refletir tensão, corrente e impedância a partir da relação de transformação do transformador, vamos dar um passo adiante e estudar sistemas um pouco mais complexos.
A gente vai estudar sistemas com um ou mais transformadores que alimentam uma determinada carga, podendo ter fator de potência indutivo ou capacitivo e aprender a calcular a regulação de tensão do transformador. Vem comigo!
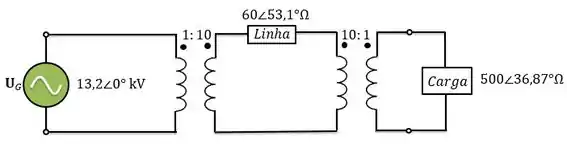
No sistema abaixo, a fonte alimenta um transformador de através de uma linha de transmissão. A impedância série do circuito equivalente do transformador referida para o lado de baixa é . O transformador está conectado com uma carga de com fator de potência igual a atrasado que possui tensão de .
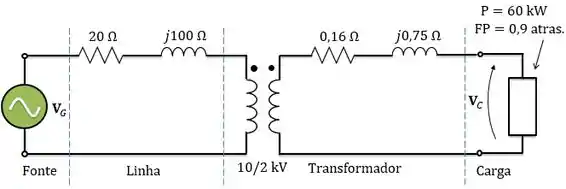
Nossa missão é calcular a tensão da fonte e a regulação de tensão do sistema e a sua eficiência. Vamos por partes.
Passo 1:
Primeiro vamos encontrar a tensão na fonte. Podemos fazer isso de duas maneiras, passando o sistema para o sistema pu ou passando todo o sistema para o secundário do transformador através da relação de transformação. Vamos fazer pela segunda maneira.
A relação de transformação desse transformador é
Passo 2:
A tensão da fonte refletida para o secundário do transformador será:
Já a impedância da linha refletida será:
Passo 3:
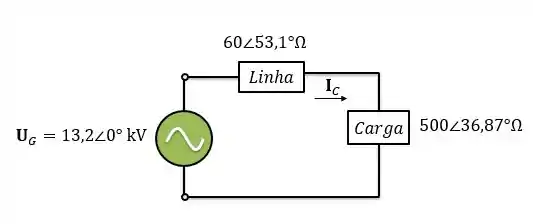
Então, temos o seguinte modelo com todas as grandezas refletidas para o secundário:
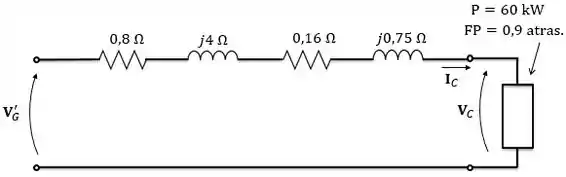
Vamos considerar que a tensão da carga está na referência, ou seja, seu ângulo é zero:
Como o transformador alimenta uma carga com e atrasado, podemos encontrar o conjugado da corrente na carga.
Como,
E
Além disso, o ângulo da potência complexa é o ângulo do fator de potência. Como o fator de potência é atrasado, a carga é predominantemente indutiva e seu ângulo é positivo.
Então, calculando a corrente da carga:
Passo 4:
Agora é aplicar a lei das tensões de Kirchhoff na malha do circuito:
Passo 5:
Encontramos a tensão da fonte refletida para o secundário, temos que refleti-la para o primário:
Regulação de tensão
A regulação de tensão é definida como a variação de tensão no secundário quando se passa da condição sem carga para carga total ou plena carga. Ela é calculada pela seguinte fórmula:
Pela fórmula, a gente nota que para o cálculo da regulação só se utiliza os módulos das tensões.
No nosso circuito, quando a carga está ligada, a tensão nos terminais do secundário é igual à tensão que está sendo aplicada na carga. Logo,
Agora, vamos analisar a condição sem carga. Quando não há carga conectada ao secundário, ou seja, quando o transformador está a vazio, a gente considera, para o cálculo da regulação de tensão, que a tensão da entrada do sistema permanece constante. Então, temos o circuito abaixo:
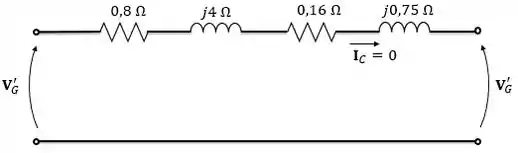
Como o circuito está aberto, não tem circulação de corrente, logo não há queda de tensão nas impedâncias do circuito e toda a tensão refletida do primário é aplicada nos terminais do secundário. Logo,
Então, a regulação de tensão desse sistema será:
Antes de continuar e calcular o rendimento do sistema temos que tomar cuidado, pois a regulação de tensão do sistema nem sempre é a regulação de tensão do transformador.
Nesse exemplo, queríamos determinar a regulação de tensão do sistema que é constituído pelo transformador mais a linha de transmissão.
Se quiséssemos calcular a regulação de tensão apenas do transformador, teríamos que considerar a tensão após a queda de tensão na impedância da linha. Se liga no circuito abaixo:
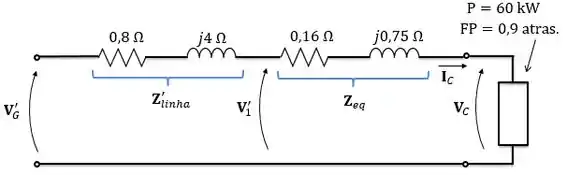
Então, a tensão do primário refletida seria:
Então, a regulação de tensão do transformador será:
Eficiência ou rendimento
O rendimento de um sistema ou de um transformador é definido como sendo
Em que a potência de entrada é a soma da potência de saída somado com as perdas na linha de transmissão e no enrolamento do transformador.
Da mesma forma que a regulação de tensão, se queremos calcular o rendimento do sistema, devemos considerar a perda de todos os elementos do sistema (linha de transmissão + transformador).
Nosso sistema é esse:
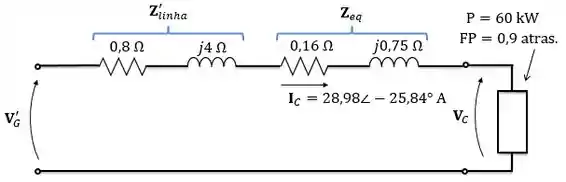
A potência de saída é a potência ativa na carga, ou seja,
Já as perdas estão relacionadas às resistências da linha e do transformador. Logo,
Então, a potência de entrada será:
Logo, o rendimento do sistema será:
Pronto! Missão cumprida!
Também podemos resolver sistemas com transformadores utilizando o sistema PU. Normalmente quando um sistema possui mais de um transformador, nós resolvemos em pu.
Como vimos no tópico de sistema PU, não precisamos ficar refletindo o circuito para um lado ou o outro dos transformadores. A gente trabalha sem se preocupar com isso e depois basta multiplicarmos pelas bases que determinamos para encontrar os valores em e .
Agora vamos destruir os exercícios!
Regulação de tensão
Eficiência ou rendimento
Exercícios Resolvidos
Exercício Resolvido #1
Livro Chapman, p. 144, Problema 2.2
Um sistema de potência monofásico está mostrado na figura abaixo. A fonte de potência alimenta um transformador de e por meio de uma impedância de alimentador de . A impedância em série equivalente do transformador, referida ao seu lado de baixa tensão, é . A carga no transformador é com FP atrasado e .
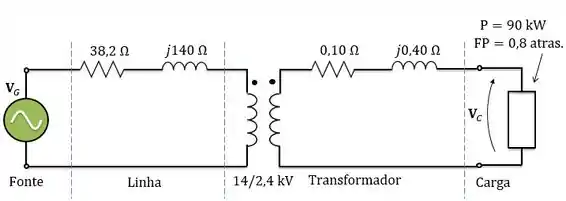
Qual é a tensão na fonte de potência do sistema?
Qual é a regulação do transformador?
Qual é a eficiência do sistema de potência?
Passo 1
Na letra o que ele quer saber é o valor da tensão da fonte. Então, primeiro temos que achar a relação de transformação:
Passo 2
A impedância da linha refletida para o secundário será:
Passo 3
Lembrando que:
Assim:
Como foi dito que o FP está atrasado, significa que a corrente está atrasada da tensão e, portanto, o ângulo do FP é positivo (carga predominantemente indutiva).
Então, calculando a potência aparente na carga:
Logo,
Passo 4
Agora já podemos encontrar o conjugado da corrente na carga:
Vamos considerar que a tensão da carga está na referência, ou seja, seu ângulo é zero:
Logo, calculando a corrente na carga:
Logo, a corrente na carga será:
Passo 5
Pela Lei das Tensões de Kircchoff, teremos que:
Passo 6
Como a tensão calculada no passo anterior é a tensão da fonte referida para o secundário, temos que voltar com ela para o primário novamente para encontrarmos o valor da tensão da fonte real:
Passo 7
Para calcularmos a regulação de tensão apenas do transformador, temos que considerar a tensão após a queda de tensão na impedância da linha:
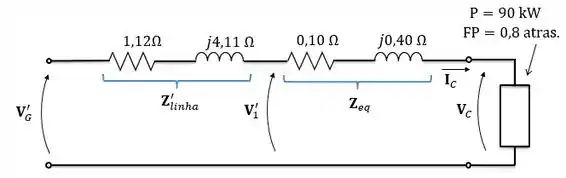
Passo 8
Portanto, a regulação de tensão do transformador será:
Passo 9
A eficiência do sistema de potência vai ser:
A potência de saída é aquela que chega à carga. Ou seja:
Para o cálculo da potência de entrada, temos que levar em consideração as perdas. Logo:
As perdas estão relacionadas às resistências da linha e do transformador. Logo,
Logo:
A eficiência do transformador será, então:
Resposta
Exercício Resolvido #2
Livro Chapman, p. 145, problema 2.3 (adaptada)
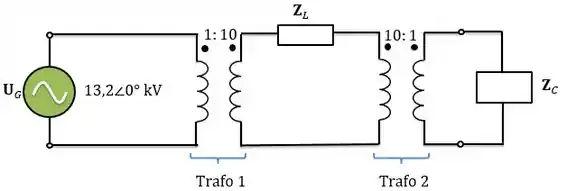
Considere um sistema de potência simples consistindo em uma fonte ideal de tensão, um transformador elevador ideal, uma linha de transmissão, um transformador abaixador ideal e uma carga. A tensão da fonte é A impedância da linha de transmissão é e a impedância da carga é .
Assuma que os transformadores não estão presentes no circuito. Qual é a tensão da carga e a eficiência do sistema?
Assuma que o transformador é um transformador elevador e que o transformadoré um transformador abaixador . Qual é a tensão da carga e a eficiência do sistema?
Passo 1
Na letra ele pede para desconsiderar os dois transformadores. Então o circuito será:

Pela Lei de Ohm, a corrente na carga será:
Logo, a tensão da carga será:
Passo 2
Para calcular a eficiência do sistema, fazemos:
Lembrando que as perdas ocorrem da linha de transmissão, a potência de entrada será:
Logo, a eficiência será:
Passo 3
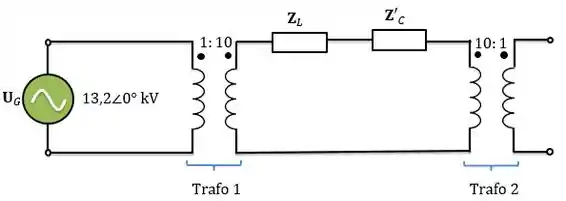
Na letra ele se refere ao circuito abaixo: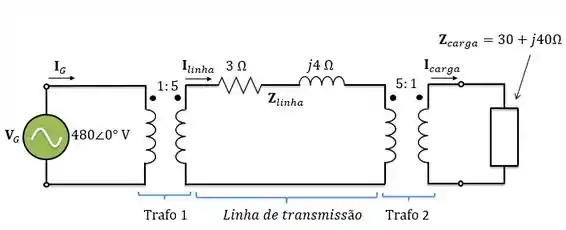
Como a gente quer saber a tensão em cima da carga, vamos refletir tudo para o primário do transformador 1.
A relação de transformação do transformador 1 é:
A relação de transformação do transformador 2 é:
Refletindo a carga do secundário para o primário do transformador 2:
Até então o circuito está assim:
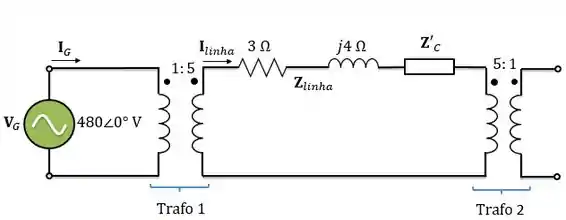
Agora, temos que refletir a impedância da carga novamente, mas desta vez para o primário do transformador 1 . Então:
Substituindo a equação na equação :
Logo:
Esse resultado é interessante, porque diz que a impedância do secundário do transformador 2 é igual à impedância refletida para o primário do transformador 1. Mas por que isso aconteceu?
Se a gente notar, as relações de transformação têm valores inversos. Isso faz com que, no final de tudo, elas simplifiquem. Então:
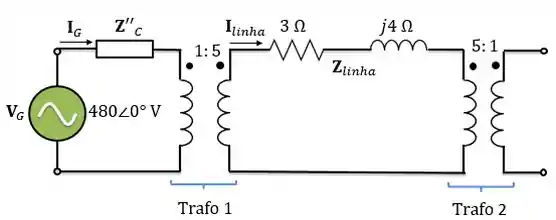
Passo 4
Agora falta a gente refletir a impedância da linha do secundário para o primário do transformador 1. Então:
Passo 5
Para calcularmos a corrente que circula no circuito abaixo, utilizamos a Lei de Ohm:
Passo 6
Logo, a tensão na carga será:
Passo 7
Agora vamos calcular a eficiência do sistema:
A potência de entrada tem que levar em consideração as perdas na linha de transmissão:
Portanto, a eficiência será:
Resposta
Exercício Resolvido #3
Lista professor João Salvador, UFRJ, Ex. 3
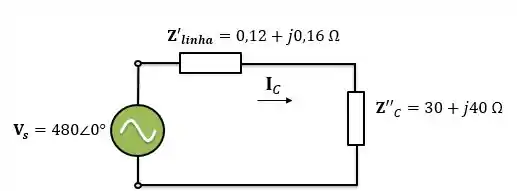
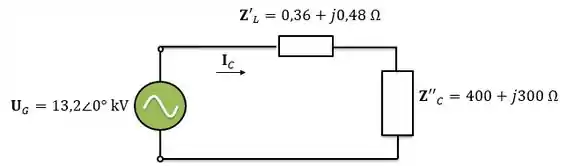
Um gerador monofásico de alimenta uma carga através de uma linha de transmissão. A impedância da carga é e da linha é .
Se um gerador for conectado diretamente à carga como no circuito abaixo, qual é a razão entre a tensão da carga e a tensão gerada ? Quais os valores das perdas do sistema?
Se dois transformadores forem colocados no sistema conforme o circuito abaixo, qual será o valor da nova razão entre as tensões da carga e do gerador? Quais os valores das perdas no sistema agora? (Os transformadores podem ser considerados ideais)
Passo 1
Para fazer letra primeiro temos que encontrar a corrente do circuito:
Pela Lei de Ohm, a corrente na carga será:
Passo 2
A tensão da carga será:
Passo 3
A razão entre a tensão da carga e do gerador será:
Isso significa que a tensão da carga é da tensão do gerador.
Passo 4
As perdas do sistema serão causadas pela resistência da linha de transmissão. Então:
A resistência da linha será:
Logo:
Passo 5
Para a letra precisaremos calcular a nova tensão em cima da carga.
Como a gente quer saber a tensão em cima da carga, vamos refletir tudo para o primário do transformador 1.
A relação de transformação do transformador 1 é:
A relação de transformação do transformador 2 é:
Refletindo a carga do secundário para o primário do transformador 2:
Até então o circuito está assim:
Agora, temos que refletir a impedância da carga novamente, mas desta vez para o primário do transformador 1 . Então:
Substituindo a equação na equação :
Logo:
Esse resultado é interessante, porque diz que a impedância do secundário do transformador 2 é igual à impedância refletida para o primário do transformador 1. Mas por que isso aconteceu?
Se a gente notar, as relações de transformação têm valores inversos. Isso faz com que, no final de tudo, elas simplifiquem. Então:
Ou, ainda:
Passo 6
Agora falta a gente refletir a impedância da linha do secundário para o primário do transformador 1. Então:
Ou, ainda:
Passo 7
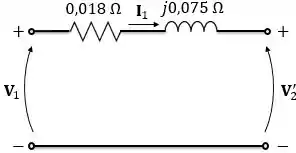
Depois de fazer todas as reflexões necessárias, temos o seguinte circuito:
Pela Lei de Ohm, a corrente do circuito será:
Passo 8
Portanto, a nova tensão na carga será:
Passo 9
Após a conexão dos dois transformadores no circuito, a nova razão entre as tensões da carga e da fonte será:
Isso significa que a tensão da carga é da tensão do gerador.
Passo 10
As perdas do sistema serão causadas pela resistência da linha de transmissão. Então:
Resposta
Exercício Resolvido #4
Livro Chapman – p.145 – Problema 2.8 (adaptado)
Um transformador monofásico de e tem uma resistência por unidade de e uma reatância por unidade de (dados tomados da placa do transformador).
Encontre o circuito equivalente, referido ao lado de baixa tensão desse transformador.
Calcule a regulação de tensão do transformador, para uma corrente de plena carga com um fator de potência de atrasado.
Passo 1
Pelo enunciado:
Como estamos trabalhando com pu, temos que encontrar o valor base das grandezas. Vamos dividir esse sistema em dois trechos (o lado do primário e o lado do secundário do transformador) e determinar as grandezas base de cada região.
Os valores em pu foram obtidos da placa do transformador. Logo, os valores bases são os valores nominais do transformador. Como a potência base é a mesma para todo o sistema.
Já para a tensão, cada lado tem uma tensão base:
Passo 2
Com esses valores bases a gente já consegue determinar os valores base para a impedância e corrente dos trechos.
Já para o trecho 2:
Passo 3
Na letra , temos que determinar o circuito equivalente referido ao lado de baixa. Então, vamos multiplicar o valor da reatância e impedância, em pu, por seus valores base do trecho 1 para encontrarmos o seu valor real em ohms, já referido ao lado de baixa (primário).
Então,
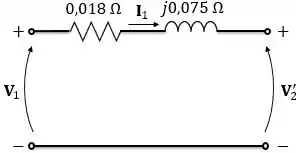
Logo, o circuito equivalente referido ao primário desse transformador será:
Passo 4
Na letra , o atrasado. Logo, a carga é predominantemente indutiva e a corrente está atrasada em relação à tensão.
Como, o ângulo será:
De acordo com o enunciado, a corrente do lado de baixa é igual à corrente nominal:
Como ela está atrasada em relação à tensão seu ângulo será negativo.
Passo 5
Utilizando a Lei das tensões de Kircchoff no circuito do primário, temos:
Considerando que está na referência, temos:
Passo 6
A regulação de tensão é dada pela relação:
A tensão a vazio é aquela quando não há carga conectada nos terminais do secundário, ou seja, não há corrente circulando e, consequentemente, não tem queda de tensão na impedância equivalente do transformador.
Logo, consideremos que toda a tensão do primário é aplicada no secundário.
Já a tensão com carga é a tensão aplicada no secundário do transformador quando a carga está conectada. Como o circuito está referido ao primário:
Então, a regulação de tensão do transformador para a carga com fator de potência unitário será:
Resposta
Exercício Resolvido #5
Lista Prof. João Salvador - UFRJ - Ex.1
No circuito abaixo, os transformadores são ideais. Calcule:
As correntes do gerador , da linha e da carga ;
A tensão na carga ;
A potência complexa entregue à carga;
As perdas na linha de transmissão.
Utilize como tensão base 480V e potência base 10kVA para a região do gerador.
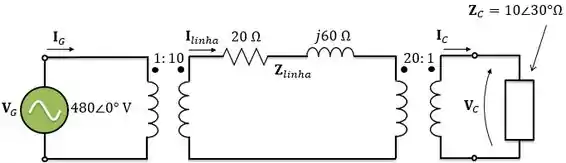
Passo 1
Como esse sistema possui mais de um transformador, vamos resolver esse exercício utilizando o sistema PU. A gente vai trabalhar sem se preocupar em refletir o circuito para um dos lados dos transformadores e depois basta multiplicarmos pelas bases que determinamos para encontrar os valores em e .
Então, como vamos trabalhar em pu, temos que encontrar o valor base das grandezas. Vamos dividir esse sistema em três regiões e determinar as grandezas base de cada região.
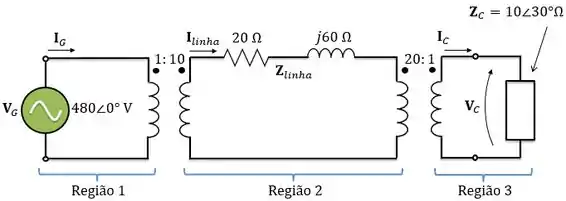
Passo 2
Para região 1 (gerador) o enunciado disse os valores de base escolhidos para esse sistema são e . Então,
Com esses valores bases a gente já consegue determinar os valores base para a impedância e corrente da região 1.
Para região 2, a potência base é a mesma, já que a gente escolhe uma para todo o circuito.
Como a relação de transformação do transformador 1 é 1:10,
A tensão base na região 2 tem que respeitar essa relação de transformação.
Então, a corrente e impedância base dessa região são:
Passo 3
A relação de transformação do segundo transformador é 20:1,
Então, respeitando a relação de transformação, a tensão base na região 3 será:
Então, a corrente e impedância base dessa região são:
Passo 4
Agora que os valores bases estão calculados, vamos passar nosso circuito inicial para pu. Para isso, pegamos o valor de cada grandeza que temos em nosso circuito e dividimos por seu respectivo valor base.
Da região 1, temos a tensão por unidade do gerador:
Da região 2, calculamos a impedância por unidade da linha:
Já da região 3, calculamos a impedância da carga em pu:
Passo 5
Agora, vamos desenhar o circuito equivalente por unidade desse sistema.
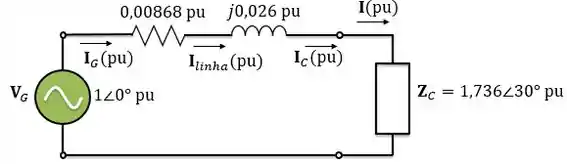
Observe que, em pu, o valor para a corrente é o mesmo em todos os trechos do sistema:
Vamos calcular essa corrente. Pela lei de Ohm:
Passo 6
Agora, precisamos encontrar as correntes em cada região do circuito em ampère. Para isso, temos que multiplicar o valor em pu pelo valor base de cada região onde está a corrente.
Então, a corrente no gerador será:
Já a corrente da linha será:
Agora, calculando a corrente da carga:
Passo 7
Na letra , temos que calcular a tensão que está sendo aplicada na carga. Logo, pela lei de Ohm:
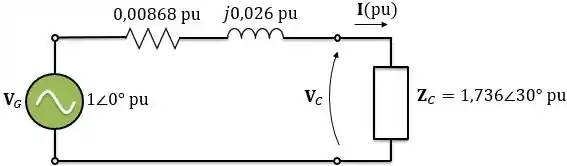
Como a carga está na região 3, o valor base da tensão da carga é . Logo, a tensão na carga em volts será:
Passo 8
Pela definição, a potência complexa entregue à carga é
Passo 9
Na letra , temos que calcular as perdas na linha de transmissão. As perdas estão relacionadas à parte resistiva da linha. Logo,
Resposta
Exercício Resolvido #6
Lista Prof. João Salvador - UFRJ - Ex.2
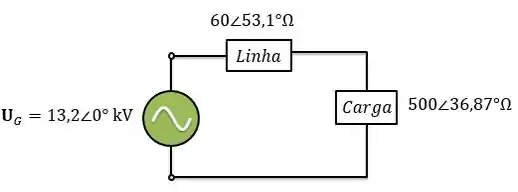
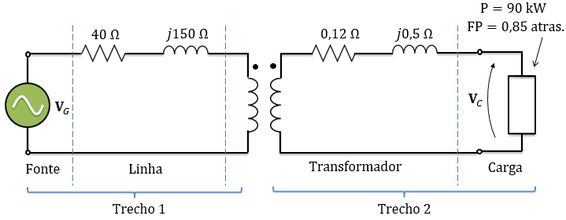
Considere o circuito abaixo. A fonte alimenta um transformador através de uma linha de transmissão. A impedância série do circuito equivalente do transformador referida ao lado de menor tensão é . A carga que está conectada ao transformador é de com fator de potência igual a atrasado, e a tensão entre seus terminais é igual a . Pergunta-se:
Qual a tensão da fonte (fasor)?
Qual é a regulação de tensão do transformador?
Qual é a eficiência total desse sistema?
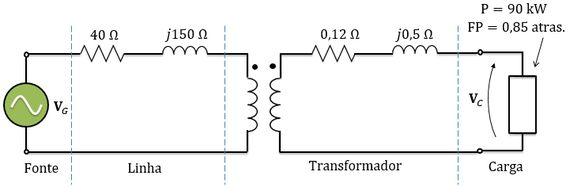
Passo 1
Já fizemos um exercício muito parecido com esse, mas, agora, vamos resolver esse exercício de uma outra maneira. Vamos resolvê-lo utilizando sistema PU.
Então, como vamos trabalhar em pu, temos que encontrar o valor base das grandezas. Podemos dividir esse sistema em dois trechos. O trecho que é o lado do primário do transformador e o trecho que corresponde ao lado do secundário.
Passo 2
Vamos escolher como bases os valores nominais do transformador. Logo a potência base escolhida para todo o sistema será:
Além disso, cada trecho vai ter uma tensão base:
Com esses valores bases a gente já consegue determinar os valores base para a impedância e corrente das duas regiões.
Passo 3
Agora que os valores bases estão calculados, vamos passar nosso circuito inicial para pu. Para isso, pegamos o valor de cada grandeza que temos em nosso circuito e dividimos por seu respectivo valor base.
Da trecho 1, calculamos a impedância por unidade da linha:
Já do trecho 2, calculamos a impedância série do circuito equivalente do transformador em pu:
Além disso, vamos considerar que a tensão da carga está na referência, ou seja, seu ângulo é zero:
Como o transformador alimenta uma carga com e atrasado, podemos encontrar o conjugado da corrente na carga.
Como,
E
Além disso, o ângulo da potência complexa é o ângulo do fator de potência. Como o fator de potência é atrasado, a carga é predominantemente indutiva e seu ângulo é positivo.
Então, calculando a corrente da carga:
Então, passando a tensão e a corrente da carga para pu:
Passo 4
Agora, vamos desenhar o circuito equivalente por unidade desse sistema.
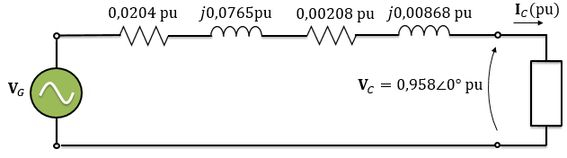
Agora é aplicar a lei das tensões de Kirchhoff na malha do circuito:
Encontramos a tensão do gerador em pu. Agora, precisamos passá-la para volts. Para isso, temos que multiplicar o valor em pu pelo valor base da tensão do gerador.
Como o gerador está no primeiro trecho, sua tensão base é . Logo,
Passo 5
Na letra , temos que tomar cuidado, pois temos que calcular a regulação de tensão do transformador e não a regulação de tensão do sistema (linha + transformador).
Então, como queremos calcular a regulação de tensão apenas do transformador, temos que considerar a tensão após a queda de tensão na impedância da linha. Se liga no circuito abaixo:
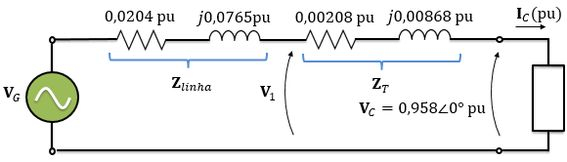
Então, a tensão do primário, em pu, será:
A regulação de tensão é calculada pela seguinte fórmula:
No nosso circuito, quando a carga está ligada, a tensão nos terminais do secundário é igual à tensão que está sendo aplicada na carga. Logo,
Já a tensão a vazio, é a tensão quando retiramos a carga, ou seja, não há corrente e, consequentemente, não tem queda de tensão na impedância equivalente do transformador. Logo, consideremos que toda a tensão do primário é aplicada no secundário.
Então, a regulação de tensão desse transformador será:
Passo 6
O rendimento de um sistema é definido como sendo
Em que a potência de entrada é a soma da potência de saída somado com as perdas na linha de transmissão e no enrolamento do transformador.
Da mesma forma que a regulação de tensão, se queremos calcular o rendimento do sistema, devemos considerar a perda de todos os elementos do sistema (linha de transmissão + transformador).
Nosso sistema é esse:
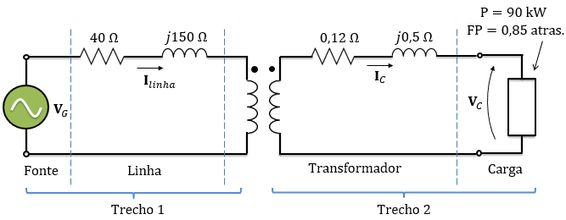
A potência de saída é a potência ativa na carga, ou seja,
Já as perdas estão relacionadas às resistências da linha e do transformador. Logo,
Então, precisamos calcular em ampéres. Como esta corrente está no trecho 1, temos:
Logo, nossas perdas serão:
Então, a potência de entrada ser��:
Finalmente, o rendimento do sistema será:
Resposta
Exercício Resolvido #7
Lista Prof. João Salvador - UFRJ - Ex.8
Medidas feitas em um transformador de , conduziram aos seguintes valores para a reatância e resistência série equivalentes referidas ao secundário (lado de baixa tensão):
A corrente de uma carga conectada ao lado de BT é igual à corrente nominal do transformador. Calcule a tensão na saída (secundário), a regulação de tensão e o rendimento do transformador quando o fator de potência da carga for igual a:
Passo 1
Antes de começar a fazer a questão, vamos desenhar o esquema do circuito:
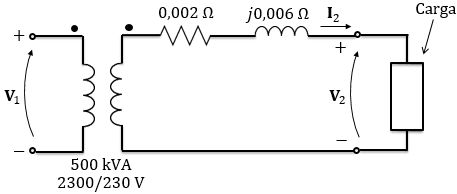
Vamos refletir a tensão do primário para o secundário para simplificarmos o circuito. A relação de transformação desse transformador é:
Então, a tensão do primário refletida para o secundário será:
Nesse exercício, vamos considerar sempre que a tensão na carga está na referência e que a tensão no primário terá uma defasagem de um ângulo em relação a ela, ou seja:
Logo, o circuito referido ao secundário será:
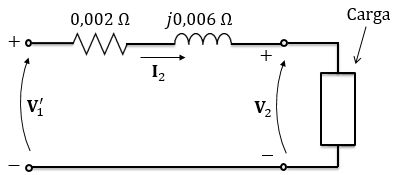
Passo 2
Lembrando que o . Se o , então , o que implica que tensão e corrente estão em fase e a carga é puramente resistiva.
De acordo com o enunciado, a corrente do lado de baixa é igual à corrente nominal:
Utilizando a Lei das tensões de Kircchoff no circuito do secundário, temos:
Passando para forma retangular:
Igualando a parte imaginária do termo à esquerda da equação com a parte imaginária do termo à direita:
Logo, o ângulo será:
Agora, igualando as partes reais:
Passo 3
A regulação de tensão é dada pela relação:
A tensão a vazio é aquela quando não há carga conectada nos terminais do secundário, ou seja, não há corrente circulando pelo secundário e, consequentemente, não tem queda de tensão na impedância equivalente do transformador.
Logo, consideremos que toda a tensão refletida do primário é aplicada no secundário.
Já a tensão com carga é a tensão aplicada no secundário do transformador quando a carga está conectada, ou seja:
Então, a regulação de tensão do transformador para a carga com fator de potência unitário será:
Passo 4
O rendimento de um transformador é definido como sendo
Em que a potência de entrada é a soma da potência de saída somado com as perdas na linha de transmissão e no enrolamento do transformador.
A potência de saída é a potência ativa na carga, ou seja,
Já as perdas estão relacionadas às resistências do transformador. Logo,
Então, a potência de entrada será:
Finalmente, calculando o rendimento:
Passo 5
Agora, o atrasado. Logo, a carga é predominantemente indutiva e a corrente está atrasada em relação à tensão.
Como, o ângulo será:
De acordo com o enunciado, a corrente do lado de baixa é igual à corrente nominal:
Só que agora seu ângulo não é zero. Como ela está atrasada em relação à tensão seu ângulo será negativo.
Passo 6
Utilizando a Lei das tensões de Kircchoff no circuito do secundário, temos:
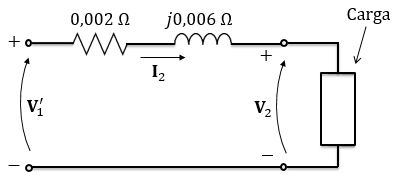
Passando para forma retangular:
Igualando a parte imaginária do termo à esquerda da equação com a parte imaginária do termo à direita:
Logo, o ângulo será:
Agora, igualando as partes reais:
Passo 7
Então, a regulação de tensão do transformador para a carga com atrasado será:
Passo 8
Sabemos que a formula do rendimento é essa:
Em que a potência de entrada é a soma da potência de saída somado com as perdas na linha de transmissão e no enrolamento do transformador.
A potência de saída é a potência ativa na carga, ou seja,
Já as perdas estão relacionadas às resistências do transformador. Logo,
Então, a potência de entrada será:
Finalmente, calculando o rendimento:
Passo 9
Na letra , o adiantado. Logo, a carga é predominantemente capacitiva e a corrente está adiantada em relação à tensão.
Como, o ângulo será:
De acordo com o enunciado, a corrente do lado de baixa é igual à corrente nominal:
Só que agora seu ângulo não é zero. Como a corrente está adiantada em relação à tensão seu ângulo será positivo.
Passo 10
Utilizando a Lei das tensões de Kircchoff no circuito do secundário, temos:
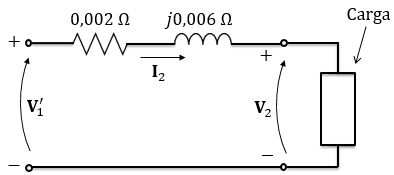
Passando para forma retangular:
Igualando a parte imaginária do termo à esquerda da equação com a parte imaginária do termo à direita:
Logo, o ângulo será:
Agora, igualando as partes reais:
Passo 11
Então, a regulação de tensão do transformador para a carga com adiantado será:
Não se espante com o sinal de menos! A regulação de tensão para cargas predominantemente capacitivas pode dar valor negativo.
Passo 12
Sabemos que a formula do rendimento é essa:
Como,
A potência de saída é a potência ativa na carga, ou seja,
Já as perdas estão relacionadas às resistências do transformador. Logo,
Então, a potência de entrada será:
Finalmente, calculando o rendimento: