Sistema por Unidade
Produzido por Alexandre NunesTeoria
Já pensou como seria mais rápido se não precisássemos transformar corrente, tensões e impedâncias do primário para o secundário e vice-versa?
Então! Com o Sistema por Unidade (PU) a gente pode resolver circuitos com transformadores sem se preocupar com as relações de transformação.
Está duvidando? Vou te provar com um exemplo! Primeiro vamos resolvê-lo da maneira tradicional e depois trabalhando com PU.
No circuito abaixo, temos um gerador de alimentando um transformador de , com impedância equivalente referida ao primário. O secundário desse transformador alimenta uma carga de . Nossa missão é encontrar as correntes do primário e do secundário desse transformador.
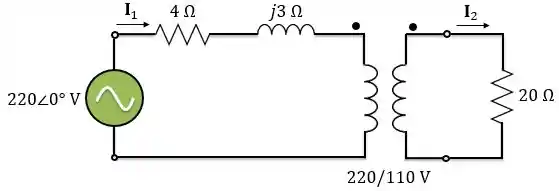
Primeiro, vamos trabalhar da maneira tradicional em e .
Passo 1:
A relação de transformação é de 2 para 1, ou seja:
Refletindo o resistor de para o primário, temos:
Passo 2:
Agora que temos todos os elementos referidos ao primário, temos que analisar o circuito abaixo:
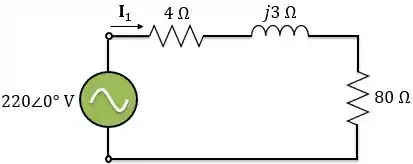
Aplicando a lei de Ohm:
Passo 3:
Vamos usar a relação de transformação mais uma vez para encontrar a corrente no secundário.
Logo,
Agora vamos trabalhar no sistema por unidade (PU).
Passo 1:
Nosso primeiro passo é escolher o valor base das grandezas. Nós escolhemos uma potência base para todo o sistema. Quando temos apenas um transformador sempre escolhemos a potência do transformador como potência base.
Agora escolhemos um valor de tensão base para cada trecho do sistema, ou seja, para cada lado do transformador. Sempre procuramos escolher as tensões nominais do transformador!
Passo 2:
Agora que temos os valores bases de potência e tensão, temos que calcular as bases para a corrente e impedância de cada trecho. Faremos isso utilizando aquelas fórmulas já batidas:
Então, as correntes de base serão:
Já as impedâncias de base:
Passo 3:
Agora que todos os valores bases estão calculados, vamos passar nosso circuito inicial para pu. Para isso, pegamos o valor de cada grandeza que temos em nosso circuito e dividimos por seu respectivo valor base.
Começamos pela tensão do gerador. Como ele está no lado do primário do transformador seu valor base é , então seu valor em pu será:
Agora, vamos fazer o mesmo para as impedâncias:
Passo 4:
Como todas as grandezas estão em pu, podemos analisar diretamente o circuito abaixo:
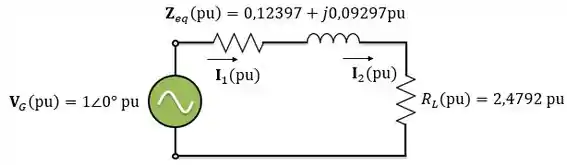
Observe que, em pu, o valor para a corrente é o mesmo em todos os trechos do sistema:
Então, pela lei de Ohm:
Passo 5:
Para terminar, precisamos encontrar a corrente em ampères. Para isso, temos que multiplicar o valor em pu pelo valor base:
Então,
Pronto! Viu só? Utilizamos o sistema pu e encontramos as mesmas respostas sem precisar fazer reflexões de impedância, tensão e corrente.
Então, para resolvermos circuitos utilizando pu temos que seguir esses passos:
- Escolher os valores bases de duas grandezas.
- A partir dos valores bases escolhidos, calcular as bases para as demais grandezas utilizando as fórmulas já conhecidas:
- Passar o circuito inicial para pu. Para isso, pegamos o valor de cada grandeza que temos em nosso circuito e dividimos por seu respectivo valor base.
- Com todas as grandezas em pu, podemos analisar o circuito e calcular o que se quer em pu.
- Para terminar, precisamos passar a grandeza calculada em pu para as unidades tradicionais e . Para isso, temos que multiplicar o valor em pu pelo valor base:
Seguindo esses passos não tem erro! Agora é fazer bastante exercícios!
Exercícios Resolvidos
Exercício Resolvido #1
Livro Fitzgerald – p.108 – Problema prático 2.10
Um transformador de e tem uma impedância em série equivalente de por unidade. Calcule a impedância em série equivalente em ohms referida ao lado de baixa e referida ao lado de alta tensão.
Passo 1
Em pu o valor da impedância equivalente do transformador, calculada por qualquer um dos lados, é único. Logo, temos o circuito equivalente abaixo para o transformador:
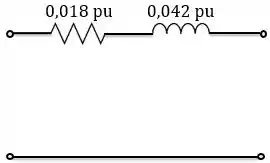
Passo 2
Como estamos trabalhando com pu, temos que encontrar o valor base das grandezas. Quando temos apenas um transformador sempre escolhemos a potência do transformador como potência base.
Agora escolhemos um valor de tensão base para cada trecho do sistema, ou seja, para cada lado do transformador. Sempre procuramos escolher as tensões nominais do transformador!
Passo 3
Com esses valores bases a gente já consegue determinar os valores base para as impedâncias do primário e secundário.
Passo 4
Agora, precisamos encontrar as impedâncias referidas para o primário e secundário em ohms. Para isso, temos que multiplicar o valor em pu pelo valor base:
A impedância referida para o lado de baixa (primário) será:
Passo 5
Já a impedância referida para o lado de alta (secundário) será:
Resposta
Exercício Resolvido #2
Livro Fitzgerald – p.106 – ex. 2.12 (adaptado)
O circuito equivalente de um transformador de e está mostrado abaixo:
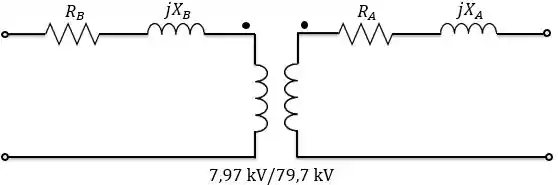
Os parâmetros do circuito equivalente são:
Converta os parâmetros do circuito equivalente para a forma por unidade usando as especificações nominais do transformador como base.
Passo 1
Como queremos trabalhar com pu, temos que encontrar o valor base das grandezas. Escolhendo a potência do transformador como potência base:
Agora escolhemos um valor de tensão base para cada trecho do sistema, ou seja, para cada lado do transformador. Escolhendo as tensões nominais do transformador:
Passo 2
Com esses valores bases a gente já consegue determinar os valores base para as impedâncias do primário e secundário.
Passo 3
Agora que os valores bases estão calculados, vamos passar nosso circuito inicial para pu. Para isso, pegamos o valor de cada grandeza que temos em nosso circuito e dividimos por seu respectivo valor base.
A impedância, em pu, para o lado de baixa (primário) será:
Já a impedância, em pu, para o lado de alta (secundário) será:
Passo 4
Então, em pu, temos o circuito equivalente abaixo:
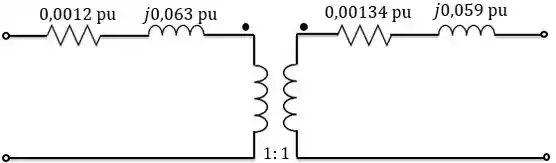
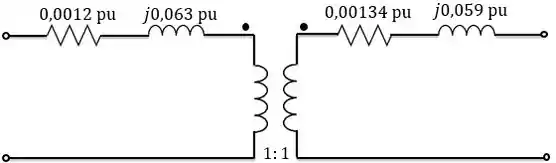
Como todo o circuito está em pu, não precisamos nos preocupar com a reflexão de impedâncias, já que, em pu, a relação de transformação é . Então, podemos omitir o transformador ideal e considerar o circuito equivalente abaixo para o transformador:
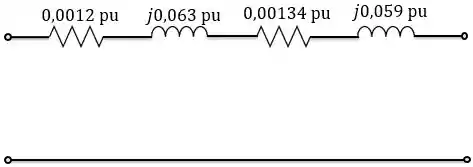
Resposta
Exercício Resolvido #3
Material do professor Heloi Moreira – UFRJ - Ex. 2 (adaptado)
Um transformador de e possui reatância de dispersão do enrolamento de alta de , equanto que a correspondente do lado de BT é igual a . Determinar o circuito equivalente do transformador em pu considerando como bases as suas grandezas nominais.
Passo 1
O primeiro passo é escolher o valor base das grandezas. Escolhemos uma potência base para todo o sistema:
Agora, as tensões base:
Passo 2
Para calcular as impedâncias base, fazemos o seguinte:
Para o secundário:
Passo 3
Agora já conseguimos calcular o valor das impedâncias em pu:
Para o primário:
Para o secundário:
Passo 4
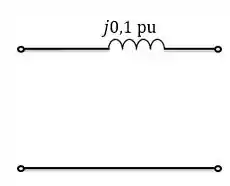
A impedância equivalente do circuito será, então:
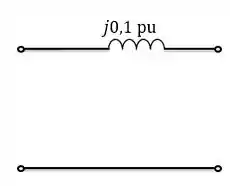
Resposta
Exercício Resolvido #4
Livro Fitzgerald – p.106 – Problema 2.34 (adaptado)
Um transformador monofásico de , e tem impedâncias de primário e secundário de por unidade cada. Todas as grandezas são por unidade na base do transformador. Calcule as resistências e as reatâncias do primário e do secundário em ohms.
Passo 1
Como estamos trabalhando com pu, temos que encontrar o valor base das grandezas. Como o enunciado disse que todas as grandezas estão na base do transformador, escolhemos seus valores nominais como base.
Escolhendo a potência do transformador como potência base:
Agora escolhemos um valor de tensão base para cada trecho do sistema, ou seja, para cada lado do transformador. Escolhendo as tensões nominais do transformador:
Passo 2
Com esses valores bases a gente já consegue determinar os valores base para as impedâncias do primário e secundário.
Passo 3
Agora, precisamos encontrar as impedâncias referidas para o primário e secundário em ohms. Para isso, temos que multiplicar o valor em pu pelo valor base:
A impedância do primário será:
Logo, a resistência e reatância do primário, em ohms, são:
Já a impedância do secundário será:
Logo, a resistência e reatância do secundário, em ohms, são:
Resposta
Exercício Resolvido #5
Livro Chapman – p.95 – ex2.3 (adaptado)
A figura abaixo mostra um sistema de potência simples. Esse sistema contém um gerador de ligado a um transformador elevador ideal 1:10, uma linha de transmissão, um transformador abaixador ideal 20:1 e uma carga. A impedância da linha de transmissão é e a impedância da carga é . Os valores de base escolhidos para esse sistema são e no gerador.
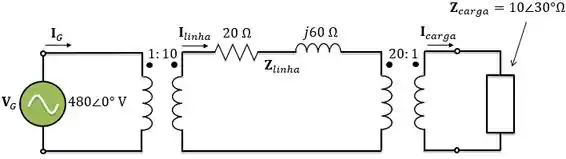
Encontre a tensão, a corrente, a impedância e a potência aparente, todos de base, em cada ponto do sistema de potência.
Converta esse sistema para seu circuito equivalente por unidade.
Passo 1
Como estamos trabalhando com pu, temos que encontrar o valor base das grandezas. Vamos dividir esse sistema em três regiões e determinar as grandezas base de cada região.
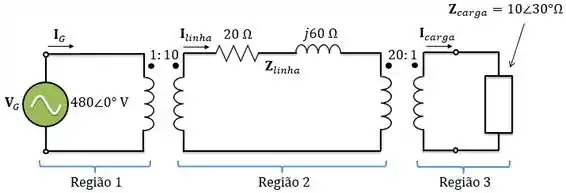
Para região 1 (gerador) o enunciado disse os valores de base escolhidos para esse sistema são e . Então,
Com esses valores bases a gente já consegue determinar os valores base para a impedância e corrente da região 1.
Passo 2
Para região 2, a potência base é a mesma, já que a gente escolhe uma para todo o circuito.
Como a relação de transformação do transformador 1 é 1:10,
A tensão base na região 2 tem que respeitar essa relação de transformação.
Então, a corrente e impedância base dessa região são:
Passo 3
A relação de transformação do segundo transformador é 20:1,
Então, respeitando a relação de transformação, a tensão base na região 3 será:
Então, a corrente e impedância base dessa região são:
Passo 4
Agora que os valores bases estão calculados, vamos passar nosso circuito inicial para pu. Para isso, pegamos o valor de cada grandeza que temos em nosso circuito e dividimos por seu respectivo valor base.
Da região 1, temos a tensão por unidade do gerador:
Da região 2, calculamos a impedância por unidade da linha:
Já da região 3, calculamos a impedância da carga em pu:
Passo 5
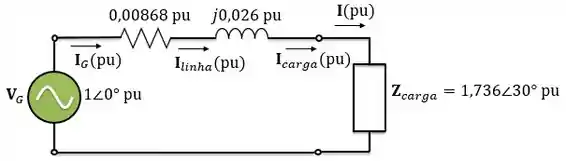
Agora, vamos desenhar o circuito equivalente por unidade desse sistema.
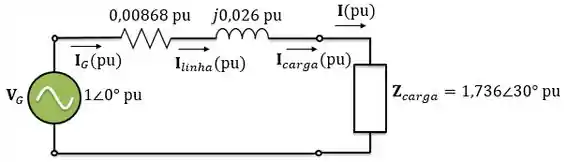
Observe que, em pu, o valor para a corrente é o mesmo em todos os trechos do sistema:
Resposta
Exercício Resolvido #6
Material Prof. Heloi – UFRJ – Ex.1
Considere um transformador monofásico ideal de , Esse transformador alimenta com tensão nominal uma carga de 48 e indutivo, instalada na . Em pu, determine as condições de operação do transformador.
Passo 1
Determinar as condições de operação do transformador, em pu, é calcular as correntes, tensões e impedâncias em pu.
Para isso, o primeiro passo é escolher o valor base das grandezas. Nós escolhemos uma potência base para todo o sistema. Quando temos apenas um transformador sempre escolhemos a potência nominal do transformador como potência base.
Agora escolhemos um valor de tensão base para cada trecho do sistema, ou seja, para cada lado do transformador. Sempre procuramos escolher as tensões nominais do transformador!
Passo 2
Agora que temos os valores bases de potência e tensão, temos que calcular as bases para a corrente e impedância de cada trecho. Faremos isso utilizando aquelas fórmulas já batidas:
Então, as correntes de base serão:
Já as impedâncias de base:
Passo 3
Agora que todos os valores bases estão calculados, vamos passar nosso circuito inicial para pu. Para isso, pegamos o valor de cada grandeza que temos em nosso circuito e dividimos por seu respectivo valor base.
Considerando que a tensão na carga está na referência, ou seja, seu ângulo é zero, temos:
Passo 4
Como o transformador alimenta uma carga com e indutivo, podemos encontrar a corrente no secundário em ampères.
Logo, passando para pu:
Passo 5
Falta encontrarmos a impedância da carga, peça lei de Ohm:
Agora, vamos passar para pu:
Resposta
Exercício Resolvido #7
Material do professor Heloi Moreira – UFRJ- Ex. 3 (adaptado)
Considere o “diagrama unifilar” de um sistema monofásico como mostrado abaixo, composto por um gerador G, um transformador elevador T1, uma linha de transmissão LT, um transformador abaixador T2 e uma carga puramente resistiva:
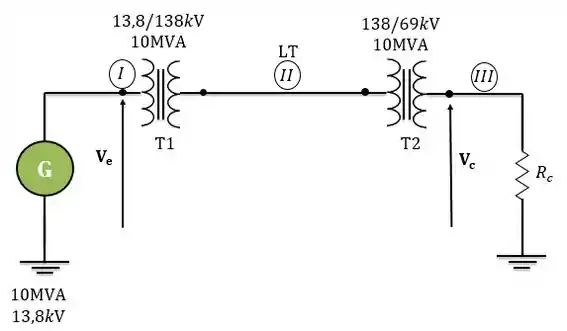
Os principais parâmetros desses equipamentos são dados abaixo:
G: gerador de
T1: transformador monofásico de impedância igual a referida para AT;
LT: Linha de transmissão com impedância de ;
T2: transformador monofásico de , , impedância igual a referida para BT;
Carga: resistência monofásica de
Condição de operação: a carga está sendo alimentada pelo transformador T2, com tensão de módulo igual a .
Determinar a tensão aplicada pelo gerador na entrada do sistema.
Passo 1
A primeira coisa que temos que fazer é determinar a potência base para todo o sistema:
Agora, precisamos encontrar as tensões base para cada trecho do circuito:
Passo 2
Da mesma forma, cada trecho terá sua impedância base:
Passo 3
Calculando as correntes base para cada trecho:
Passo 4
Agora já podemos calcular a impedâncias em pu. Lembrando que:
Para o transformador 1, como foi dito no enunciado que a impedância estava referida para o lado de AT, então significa que ela está no trecho :
Para a linha de transmissão, como ela está no trecho
Para o transformador 2, o enunciado diz que a impedância está referida para o lado de BT, que se encontra no trecho
Para a carga, que está no trecho :
Passo 5
Estamos quase terminando! Precisamos, agora, calcular a tensão da carga em pu, que está no trecho :
Adotaremos a tensão na carga como estando na referência:
A corrente na carga, em , será:
Então, o circuito em pu fica assim:
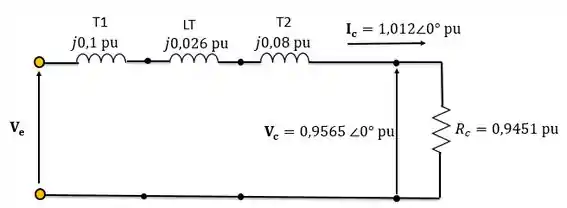
Passo 6
Como estamos interessados em determinar a tensão , utilizamos a Lei das Tensões de Kircchoff no circuito acima:
Passo 7
Finalmente, a tensão de entrada em volts, será: