Transformadores em paralelo
Produzido por Alexandre NunesTeoria
Introdução
Fala aí, pessoal, bora entender como colocar dois ou mais transformadores em paralelo para dar mais confiabilidade ao seu sistema de energia e fornecer mais energia a sua carga.
Mas o que precisamos saber para colocar dois transformadores em paralelo?
Condições
Como vamos conectar os lados primários entre si e os lados secundários entre si devemos obedecer a algumas condições para colocar dois transformadores em paralelo:
Primeira condição: mesma relação de transformação “a” e mesma tensão
Como vamos conectar os primários entre si e os secundários entre si, as tensões devem ser as mesmas nos primários e nos secundários, como vamos conectar os primários na mesma fonte de tensão garantimos o primeiro quesito. Porém as relações de transformação devem ser iguais para que as tensões nos secundários sejam iguais.
Para que :
Caso isso não ocorra, teremos uma diferença de potencial entre os secundários dos transformadores e circulará corrente de um transformador para o outro.
Por exemplo, se temos um transformador de 1000V/100V e um transformador de 1000V/25V, apesar das tensões dos primários serem iguais (1000V), quando conectarmos em paralelo o terá uma tensão de secundário igual a 100V, enquanto o terá uma tensão igual a 25V. Essa diferença de tensão irá provocar circulação de corrente entre eles.
Segunda condição: mesmo defasamento angular
Bom como já falamos antes, queremos que os secundários tenham a mesma tensão e para isso temos que pensar no ângulo das tensões. Lembrando que a tensão é um fasor, que tem tanto módulo quanto ângulo de defasagem.
Podemos ligar o transformador de várias formas, como já vimos anteriormente: Y-Δ, Y-Y, Δ-Y, Δ- Δ, Y-Z...
Sabemos então que existe um defasamento dos ângulos entre primário e secundário, como por exemplo adiantamos 30˚ as tensões dos secundários quando temos uma conexão Y- Δ.
Precisamos garantir que o módulo da tensão e a defasagem sejam as mesmas, por exemplo: se a tensão de um transformador tem como tensão de secundário , enquanto o transformador tem como tensão de secundário . Temos a diferença de tensão:
Logo como existe essa diferença de potencial, ocorre a circulação de corrente entre um transformador e o outro, algo que não desejamos.
Mas caso as duas tensões fossem iguais a , essa diferença seria 0V e não circularia corrente.
Terceira condição: mesma sequência de fase
Bom pessoal, como já falamos até agora o secundário e o primário devem ter as mesmas tensões entre si. Para isso temos que considerar a sequência de fase, pois ela nos fala sobre os ângulos das outras fases após determinarmos um ângulo de referência.
Na sequência positiva ou ABC, temos:
Na sequência negativa ou ACB, temos:
Assim, a sequência de fase deve ser igual para os dois transformadores para que nunca ocorra diferença de ângulo nas tensões da mesma fase.
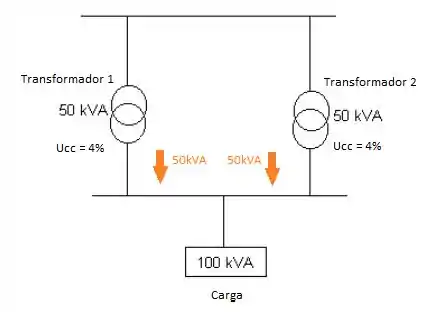
Quarta condição: mesma tensão de curto-circuito
Colocando dois transformadores em paralelo para suprir uma carga, a corrente que a carga solicita irá se dividir entre os transformadores de acordo com as impedâncias internas dos transformadores.
Caso elas sejam iguais, cada um contribuirá com a mesma potência. Se não forem, passará mais corrente pelo transformador que tiver a menor impedância, assim apenas um transformador irá alimentar a carga.
Primeira condição: mesma relação de transformação “a” e mesma tensão
Segunda condição: mesmo defasamento angular
Terceira condição: mesma sequência de fase
Quarta condição: mesma tensão de curto-circuito
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Caso você precise verificar a condição de sequência de fase para colocar dois transformadores em paralelo, mas não tem o equipamento adequado. Qual seria uma solução possível?
Passo 1
Caso você não tenha acesso ao sequencímetro que verifica a sequência de fase do equipamento, mas possa utilizar um motor assíncrono comum, podemos ligar o motor em cada um dos transformadores da mesma maneira, ou seja ligando as fases do lado secundário da mesma maneira no motor.
Passo 2
Devemos verificar se o motor vai girar nos dois casos pro mesmo lado, se sim temos a mesma sequência de fase. Se o motor não girar pro mesmo lado nas duas situações, temos então duas sequências de fase.
Passo 3
Para colocar dois transformadores em paralelo, temos que ter a mesma sequência de fase. Mas como trocar a sequência se forem duas diferentes?
Em um dos transformadores, trocamos duas das fases conectadas do lado primário e assim todos os dois transformadores estarão na mesma sequência de fases.
Resposta
Utilizar um motor e verificar se nos dois casos, ele gira pro mesmo lado.
Exercício Resolvido #2
Preparatório 5 – Laboratório de conversão - UFRJ
Os valores nominais e dados de curto-circuitos de um grupo de quatro transformadores monofásicos são os seguintes:

Que par destes transformadores funciona melhor em paralelo analisando as tensões de curto-circuito, através de comparação entre razões.
Passo 1
A condição para colocar dois transformadores em paralelo, devemos ter tensões de curto-circuito muito próximas, logo a razão entre eles deve ser a mais próxima de 1 possível.
Passo 2
Analisando um transformador em relação ao outro:
Passo 3
A relação mais próxima de 1 é entre os transformadores A e D.
Resposta
Transformadores A e D.
Exercício Resolvido #3
Preparatório 5 – Laboratório de Conversão – UFRJ
Dois bancos de transformadores trinângulo- triângulo de transformadores monofásicos conectam em paralelo para alimentar uma carga equilibrada composta de três resistências conectadas em estrela aos terminais de baixa tensão do sistema. Cada resistência é de 0,088Ω. Os valores nominais de cada um dos seis transformadores monofásicos são: 100kVA, 11500:230V, 60Hz. Pode-se considerar os transformadores de cada banco exatamente iguais e com impedância de curto-circuito dada pela tabela a seguir.

Pede-se:
- Modelar os bancos de transformadores por equivalentes monofásicos e refletir impedâncias par o lado da carga.
- Conectar os bancos em paralelo através de seus modelos equivalentes e resolver o circuito de forma completa e sem simplificações. Aplique tensões senoidais equilibradas nominais ao primário da conexão. Quais são as intensidades de corrente das fases que circulam pela carga.
Passo 1
Primeiro preciamos calcular os parâmetros da impedância de cada um dos bancos de transformadores. Para isso vamos utilizar os dados do ensaio de curto-circuito da tabela.
Banco A:
Banco B:
Passo 2
Como a carga está posicionada no lado de baixa dos transformadores, temos que refletir as impedências encontradas para o lado de baixa do transformador:
Refletindo as impedâncias do banco A:
Refletindo as impedâncias do banco B:
Completamos os quesitos da letra “a”, agora vamos para a letra “b”.
Passo 3
Para conectarmos a carga em Y em paralelo com os transformadores em Δ, vamos transformar a carga para Δ:
Passo 4
Se supormos que a tensão na carga é igual a , a corrente na carga será:
Como a relação de transformação é a mesma, podemos realizar um divisor de corrente entre os dois transformadores do lado secundário:
Passo 5
Com a corrente de secundário, podemos encontrar a tensão do lado primário refletido para o lado secundário:
Referindo essa tensão para o lado primário, temos que a tensão:
Passo 6
Como queríamos alimentar nossos transformadores com uma tensão: .
Sabemos que temos que fazer as seguintes modificações:
- Multiplicar todas as grandezas por
- Subtrair de todos os ângulos
Logo a corrente de carga nova é:
Essa corrente corresponde a corrente para uma carga em Δ, para a carga em Y devemos realizar as seguintes mudanças:
- Multiplicar por
- Atrasar a corrente em
Resposta
-
A:
B:
Exercício Resolvido #4
Elaboração própria
Dois transformadores serão ligados em paralelo, porém descobrimos que enquanto o primeiro segue a sequência de fase positiva, o segundo transformador segue uma sequência de fase negativa. Ambas os transformadores tem amplitude de tensão igual a 20V. Se um aluno conectar um voltímetro entre as fases A dos dois transformadores, B dos dois transformadores e C dos dois transformadores, qual será o valor medido em cada um dos voltímetros.
Passo 1
O primeiro transformador segue uma sequência de fases positiva, logo podemos escrever as tensões como:
Passo 2
O segundo transformador segue uma sequência de fases negativa, logo podemos escrever as tensões como:
Passo 3
Assim podemos calcular a tensão que cada voltímetro fazendo a diferença de cada fase, para fase A:
Passo 4
Para fase B:
Passo 5
Para fase C:
Resposta
O voltímetro ligado entre as fases A:
O voltímetro ligado entre as fases A:
O voltímetro ligado entre as fases A: