(Wankat, 3 ed. – Cap. 13 – D2) Deseja-se extrair uma solução diluída de proteína de uma solução aquosa de em massa de poli(glicol etilênico) (PEG) utilizando uma solução aquosa de em massa de dextrano. Sistemas de extração com duas fases aquosas são utilizados para recuperação de proteínas pois evitam a desnaturação da proteína, já que ambas as fases são aquosas. As duas fases podem ser consideradas imiscíveis.
A fase com dextrano é mais densa e será o solvente. A vazão da alimentação é de e a vazão de solvente é de , escoando em contracorrente com a alimentação em estágios.
O coeficiente de distribuição de proteína é (fração mássica de proteína em PEG, )/(fração mássica de proteína em dextrano, ) Qual a recuperação total de proteína na fase de solvente?
Passo 1
Faaaala aíi, tudo beleza? Nessa questão nós precisamos encontrar a recuperação total de proteína na fase de solvente considerando sistemas de extração com duas fases aquosas. Para isso, temos dois estágios conforme demostrando abaixo:
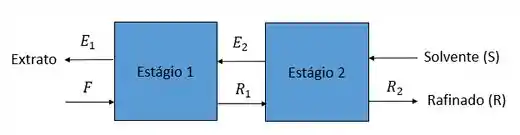
Onde,
Passo 2
Para encontrar a recuperação total de proteína na fase de solvente precisamos inicialmente fazer um balanço de massa começando pelo primeiro estágio,
Pelo coeficiente de distribuição temos,
Logo,
Passo 3
Fazendo um balanço agora para o segundo estágios temos,
Pelo coeficiente de distribuição temos,
Logo,
Passo 4
Substituindo a última expressão do passo 2 na última expressão do passo 3 temos,
Sabendo que,
Podemos substituir os valores e obter,
Passo 5
Assim, a recuperação pode ser obtida por,
Manipulando as equações e substituindo os valores temos,
Logo, a recuperação é: