Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 84

5.84 Considere novamente o escoamento viscométrico do Exemplo 5.7. Avalie a taxa média de rotação de um par de segmentos de linhas perpendiculares, orientados a ± 45 ° em relação ao eixo x. Mostre que os resultados são os mesmos do exemplo.

Passo 1

Considerando estado estacionário e escoamento incompressível.

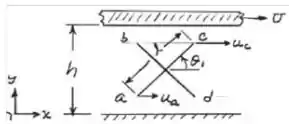
Pelo desenho acima temos:

u c = u a + ∂ u ∂ y l   s e n   θ 1

A rotação, então:

- ω a c = u c - u a s e n   θ 1 l

- ω a c = ∂ u ∂ y l   s e n   θ 1 s e n   θ 1 l  

- ω a c = ∂ u ∂ y   s e n   θ 1 2

- ω a c = U h   s e n   θ 1 2

Passo 2

Agora para o outro segmento:

u d = u b + ∂ u ∂ y l   s e n   θ 2

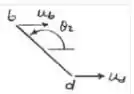
A rotação, então:

- ω b d = u d - u b s e n   θ 1 l

- ω b d = ∂ u ∂ y l   s e n   θ 2 s e n   θ 1 l

- ω b d = ∂ u ∂ y s e n   θ 2 2

- ω b d = U h s e n   θ 2 2

Passo 3

Agora é só somar os termos:

ω = 1 2 ω a c + ω b d

ω = - 1 2 U h   s e n   θ 1 2 + s e n   θ 2 2

Quando θ 1 = 45 ° e θ 2 = 135 ° ,

ω = - 1 2 U h 2 2 2 + 2 2 2

ω = - 1 2 U h

Substituindo os valores de U e h:

ω = - 1 2 4 4

ω = - 0,5   s - 1

Resposta

ω = - 0,5   s - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um campo de escoamento permanente, incompressível, sem atrito, é dado por V = 2 x yi ^ - y 2j ^ em unidades arbitrárias. Seja a massa específica ρ 0 = c o n s t a n t e e despreze a gravidade. Encontr
Um campo de escoamento incompressível, tridimensional, proposto tem a seguinte forma vetorial: V = K xi ^ + K yj ^ + 2 K zk ^ (a) Determine se esse campo é uma solução válida para a continuidade e par
A resposta para o Problema P4.14 é v θ = f ( r ) somente. Não conte isso para os seus amigos se eles ainda estiverem tentando resolver o Problema P4.14. Mostre que esse campo de escoamento é uma soluç
Considere um escoamento permanente, bidimensional, incompressível, de um fluido newtoniano no qual o capo de velocidade é conhecido: u = - 2 x y ,v = y 2 - x 2 , w = 0 . (a) Esse escoamento satisfaz a
Estude o efeito combinado dos dois escoamentos viscosos na Figura 4.12. Isto é, encontre u ( y ) quando a placa superior se move a uma velocidade V e há também um gradiente de pressão constante ( d p