Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 79

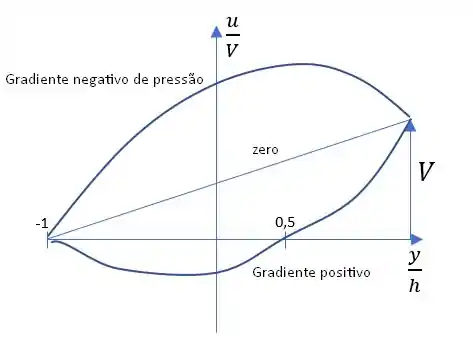
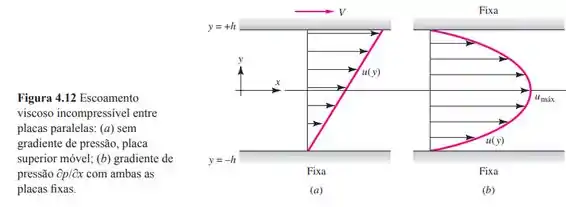
Estude o efeito combinado dos dois escoamentos viscosos na Figura 4.12. Isto é, encontre u ( y ) quando a placa superior se move a uma velocidade V e há também um gradiente de pressão constante ( d p / d x ) . É possível a superposição? Em caso afirmativo, explique por que. Faça um gráfico dos perfis de velocidade representativos para gradientes de pressão (a) zero, (b) positivo e (c) negativo para a mesma velocidade V da parede superior.

Passo 1

Bora pra mais uma!

Substituindo u = u(y) no componente x da equação da quantidade de movimento de Navier-Stokes para escoamento bidimensional (x, y):

ρ u ∂ u ∂ x + v ∂ u ∂ y = - ∂ p ∂ x - ρ g x + μ ( ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 )

Daí:

ρ 0 + 0 = - ∂ p ∂ x + 0 + μ ∂ 2 u ∂ y 2

μ ∂ 2 u ∂ y 2 - ∂ p ∂ x = 0

Desses dois termos, conforme apresentado na seção 4.10 do livro o termo μ ∂ 2 u ∂ y 2 nos dá como solução o escoamento entre placas com uma parede superior em movimento e o termo - ∂ p ∂ x o escoamento em um canal em virtude de um gradiente de pressão, daí:

u y = V 2 1 + y h + h 2 2 μ - d p d x 1 - y 2 h 2

Resposta

u y = V 2 1 + y h + h 2 2 μ - d p d x 1 - y 2 h 2

A superposição é bastante valida porque a aceleração convectiva é zero, portanto o que resta é a linear: ∇ p = μ ∇ 2 V .   Os perfis de velocidade representativos para os gradientes de pressão são representados abaixo:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Estime a velocidade à qual você precisaria nadar na água à temperatura ambiente para estar em regime de escoamento lento. (Uma estimativa da ordem de grandeza será suficiente.) Discuta.
Na derivação de uma equação de Bernoulli para regiões de escoamento sem viscosidade, usamos a identidade vetorial: V → ⋅ ∇ → V → = ∇ → V 2 2 - V → x( ∇ →xV → ) Mostre que essa identidade vetorial é sa
Combine os resultados dos Problemas 10-26 e 10-28 para mostrar que para um mancal de bloco deslizante bidimensional, o gradiente de pressão d P / d x está relacionado com a altura h do espaçamento por
Considere novamente o mancal de bloco deslizante do Problema 10-23. Faça uma análise de ordem de grandeza na equação do momento y e escreva a forma final da equação do momento y . (Sugestão: Você prec
Um bom nadador nada 100 m em aproximadamente 1 minuto. Se o corpo do nadador tiver 1,8 m de comprimento, quantos comprimentos equivalentes ao seu corpo ele nada por segundo? Repita o cálculo para o es