Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 19
Um campo de escoamento incompressível tem os componentes cilíndricos , , , em que e são constantes e , . Esse escoamento satisfaz a continuidade? O que ele pode representar fisicamente?
Passo 1
E aí, tudo bem? Bora matar essa questão rapidinho!
Vamos começar checando a equação da continuidade:
A equação da continuidade é satisfeita!
Agora vamos analizar nossas componenetes:
que varia de acordo a diferença dos quadrados, onde no centro temos a velocidade máxima e na parede a velocidade é nula!
Então podemos considerar que esse é um escoamento laminar com um torque, logo ele gira durante a queda, vamos fazer um esquema:
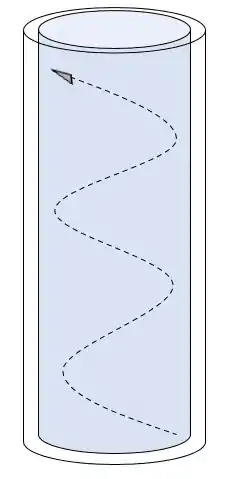
Isso é tudo pessoal, conseguimos mais uma! \o/
Resposta
Condição de continuidade é satisfeita, representa um escoamento cilíndrico com torque:
Exercícios de Livros Relacionados
5.20 Para um escoamento incompressível no plano r θ , a componente r da velocidade é dada por V r = U cos θ .(a) Determine uma possível componente θ da velocidade.(b) Quantas possíveis componentes θ
5.18 Quais dos seguintes conjuntos de equações representam possíveis casos de escoamento incompressível?(a) V r = U cos θ ; V θ = - Us e nθ (b) V r = - q / 2 π r ; V θ = K / 2 π r (c) V r = U cos
5.16 Considere um jato d’água saindo de um irrigador oscilatório de gramados. Descreva as trajetórias e as linhas de emissão correspondentes.
5.22 Um líquido viscoso é submetido a cisalhamento entre dois discos paralelos de raio R , um dos quais gira enquanto o outro permanece fixo. O campo de velocidade é puramente tangencial, e a velocida
Um fluido escoa em condições tais que sua massa específica ρ é função somente do tempo. Sendo o campo de velocidades v x = 4 x ; v y = - 2 y , determinar:A expressão de ρ ( t ) para que o escoamento s