Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 68

Para a distribuição de velocidade do Problema P4.4, (a) determine se existe um potencial de velocidade e (b) em caso afirmativo encontre uma expressão para ϕ (x, y) e faça o esboço da linha equipotencial que passa pelo ponto (x, y) = (L/2, L/2).

Distribuição do Problema P4.4:

u = U o 1 + x L         v =   - U o y L             w = 0

Passo 1

Bora pra mais uma!

  1. Vamos determinar se existe um potencial de velocidade, vamos verificar se o escoamento é irrotacional:

    2. ω z = 1 2 ∂ v ∂ x - ∂ u ∂ y = 1 2 0 - 0 = 0 .

    O escoamento é irrotacional, logo há uma função potencial. Dada por:

u = ∂ ϕ ∂ x ; v = ∂ ϕ ∂ y ; w = ∂ ϕ ∂ z

∂ ϕ ∂ x = U o 1 + x L ;   ∂ ϕ ∂ y = - U o y L ; ∂ ϕ ∂ z = 0

Integrando todas as equações:

ϕ x = U o x + U o x 2 2 L + C y , z ;   ϕ y = - U o y 2 2 L + C x , z ;   ϕ z = C o n s t

Daí, comparando-as, obtemos:

ϕ x , y = U o x + U o 2 L * x 2 - y 2 + C

Onde C é constante, para plotar a linha equipotencial vamos considera-la nula por conveniência.

Agora, vamos achar a função corrente para esboçar a linha equipotencial que passa pelo ponto (x, y) = (L/2, L/2).

∂ ψ ∂ y = u ; - ∂ ψ ∂ x = v

ψ x = U o x + U o x 2 2 L + c y ;   ψ y = - U o y 2 2 L + c x

ψ x , y = U o 2 l x 2 - y 2 + U o x

Então, podemos esboçar este ponto utilizando a ferramenta excell:

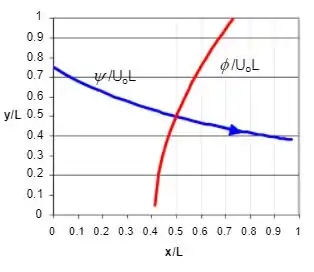
Resposta

  1. Há função potencial.

ϕ x , y = U o x + U o 2 L * x 2 - y 2 + C

Onde C é constante. A linha equipotencial que passa pelo ponto é esboçada abaixo:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o potencial de velocidades em coordenadas polares ϕ = B r 1,2c o s ( 1,2 θ ) , sendo B uma constante. Verifique se ∇ 2 ϕ = 0 . Sendo o caso, encontre a função corrente associada ψ ( r ,θ ) ,
Use o método das imagens para construir o padrão de escoamento de uma fonte 1 m próxima a duas paredes, como mostrado na Figura P 8.72 . Esboce a distribuição de velocidades ao longo da parede inferio
Construa um sistema de imagens para calcular o escoamento de uma fonte a distâncias desiguais de duas paredes, como na Figura P 8.73 . Encontre o ponto de máxima velocidade sobre o eixo y .
Discuta como o padrão de escoamento do Problema P 8.58 pode ser interpretado no sentido da construção de um sistema de imagens para paredes circulares. Por que há duas imagens em vez de uma?
Use o método de imagens para aproximar o padrão de escoamento em torno de um cilindro a uma distância 4 a de uma única parede, como na Figura P 8.76 . Para ilustrar o efeito da parede, calcule a veloc