Exercícios de Função Corrente e Função Potencial - Lista de Exercícios Resolvida

Para a distribuição de velocidades a seguir, determine se existe uma função corrente e, se existir, encontre uma expressão para e faça o esboço da linha de corrente que passa pelo ponto .

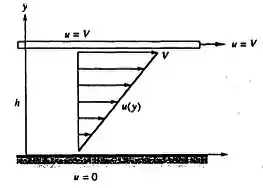
Mostre que o escoamento de Couette linear entre placas na Figura tem uma função corrente, mas não tem potencial de velocidade. Qual é a razão disso?

Um escoamento incompressível bidimensional é dado pelo campo de velocidade , em unidades arbitrárias. Esse escoamento satisfaz a continuidade? Em caso afirmativo, encontre a função corrente e faça um gráfico de algumas linhas de corrente, com setas.

Uma função corrente para um escoamento plano, irrotacional em coordenadas polares é:

Onde são constantes. Encontre o potencial de velocidade para esse escoamento.

Considere o potencial de velocidade incompressível bidimensional . É verdade que , e, em caso afirmativo, o que isso significa? Se ela existe, encontre a função corrente desse escoamento. Encontre a equação da linha de corrente que passa por .

Considere o seguinte escoamento incompressível bidimensional, que claramente satisfaz a continuidade:

Encontre a função corrente para esse escoamento usando coordenadas polares.

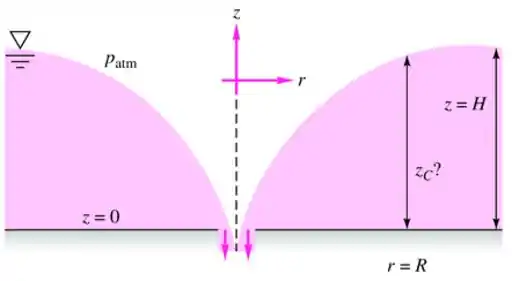
Um líquido é drenado por um pequeno furo em um tanque, como mostra a Figura, de forma que o campo de velocidade é dado por , , , em que é a profundidade da água distante do furo. Esse padrão de escoamento é rotacional ou irrotacional? Encontre a profundidade da água no raio .

Encontre o potencial de velocidade bidimensional para o padrão de escoamento em coordenadas polares , , em que e são constantes.

Um campo de escoamento incompressível bidimensional é definido pelos componentes de velocidade

em que e são constantes. Se elas existem, encontre a função corrente e o potencial de velocidade.