Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 85
Ar que escoa a , e é forçado a passar por uma curva de expansão de . Determine o número de Mach, a pressão e temperatura do ar após a expansão.
Passo 1
Esse exercício é sobre o escoamento supersônico de ar sobre uma curva de expansão de . Essa inclinação faz com que o escoamento de ar acima da curva se expanda através de ondas de expansão de Prandtl-Meyer.
A questão quer que a gente calcule o valor do número de Mach , a pressão e a temperatura do ar depois de passar pelas ondas de expansão.
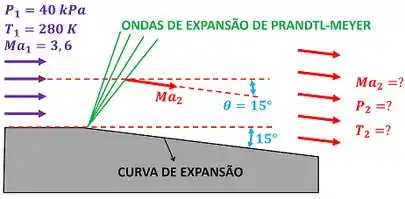
é o ângulo de virada do ar. Ou seja, é o ângulo que mede o quanto o ar varia de direção, quando atravessa o choque.
Para calcular e , precisamos saber quanto vale primeiro. Por isso, o próximo passo será todo dedicado a calcular o valor do número de Mach do ar após sua expansão.
Passo 2
Para calcular , precisamos usar uma equação de ondas de expansão que relaciona o ângulo de virada com os números de Mach e .
Atenção! não é a viscosidade cinemática do ar, nem está multiplicando e ! é um ângulo chamado de função de Prandtl-Meyer. O valor desse ângulo é uma função do número de Mach . As equações de e se encontram abaixo.
onde é uma constante que vale para o ar.
As equações acima mostram que é bem complicado achar , porque não somos capazes de isolar na equação de (colocar de um lado e tudo o que não é do outro) e calcular diretamente . Mas, calma. Existe um passo a passo pra achar .
O primeiro passo é reorganizar a equação do ângulo de virada .
Nesse novo formato, deixamos os termos que têm de um lado e os outros termos do outro.
Agora, vamos calcular quanto vale , porque o exercício já nos informou quanto vale .
Substituindo o valor de e (valor presente na imagem) na fórmula de , achamos:
Para achar o valor de a partir da equação acima, vamos precisar variar a partir do seu valor mínimo . O valor de correto é o valor onde a diferença entre os termos com e for igual a zero.
Esse valor de que faz a diferença dos termos da equação acima se anularem é igual a:
Atenção! Esse cálculo de deve ser feito com a ajuda de um algoritmo e um computador! O computador vai fazer um trabalho bem mais rápido de variar para anular a diferença dos termos e achar .
Passo 3
Nesse passo, vamos aprender a calcular ! Para fazer isso, temos que lembrar de um fato. As ondas de expansão não fazem a entropia do ar aumentar. Isso significa que o processo de atravessar essas ondas é isentrópico (a entropia é constante) e podemos usar as equações que relacionam as pressões , e (pressão de estagnação) de escoamento isentrópico.
Para não precisar calcular a pressão de estagnação , vamos inverter a equação de e multiplicá-la pela equação de . Dessa forma, vai cortar e encontraremos uma expressão para em função da pressão que já conhecemos .
Substituindo os dados na equação aima, achamos o valor de .
Passo 4
Nesse passo, vamos aprender a calcular ! Para fazer isso, podemos usar as equações que relacionam as temperaturas , e (temperatura de estagnação) de escoamento isentrópico.
Para não precisar calcular a temperatura de estagnação , vamos inverter a equação de e multiplicá-la pela equação de . Dessa forma, vai cortar e encontraremos uma expressão para em função da temperatura que já conhecemos .
Substituindo os dados na equação aima, achamos o valor de .