Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 5.Problemas - Ex. 57
A haste de aço carbono 1.040 apoiada nos suportes da Figura P5.57 está submetida a uma corrente de ar transversal a 20°C e 1 atm. Para qual velocidade U da corrente o centro da haste terá uma deflexão de aproximadamente 1 cm?
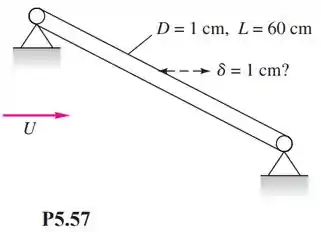
Passo 1
Vamos começar calculando a força de arrasto utilizando a equação de deflexão central de uma viga simplesmente apoiada:
Para o aço carbono (módulo de Young):
Passo 2
Agora precisamos escolher um valor arbitrário para , vamos escolher , como isso:
Vamos verificar se o valor de foi bem escolhido:
Na Figura 5.3a temos que para este valor de número de Reynolds o valor aproximado de é 1,2, ou seja, fizemos um bom chute.
Resposta
Exercícios de Livros Relacionados
Experimental data [55] for the density of n-pentane liquidfor high pressures, at 508C, are listed as follows:Pressure, kPa 100 10,230 20,700 34,310Density, kg/m3 586.3 604.1 617.8 632.8(a) Fit this da
The transfer of energy by viscous dissipation is dependentupon viscosity µ, thermal conductivity k, stream velocity U,and stream temperature T0. Group these quantities, ifpossible, into the dimensionl
The Archimedes number, Ar, used in the flow of stratifiedfluids, is a dimensionless combination of gravity g, densitydifference ∆ρ, fluid width L, and viscosity µ. Find theform of this number if it is
Flow in a pipe is often measured with an orifi ce plate, as inFig. P5.14. The volume flow Q is a function of the pressuredrop ∆p across the plate, the fluid density ρ, the pipe diameter D, and the ori
A fishnet is made of 1-mm-diameter strings knotted into2 3 2 cm squares. Estimate the horsepower required totow 300 ft2 of this netting at 3 kn in seawater at 208C. Thenet plane is normal to the flow