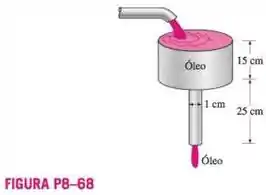
Óleo a escoa através de um funil de vidro vertical que consiste em um reservatório cilíndrico de 15 cm de altura e um tubo de 1 cm de diâmetro e 25 cm de altura. O funil sempre é mantido cheio pela adição de óleo do tanque. Supondo que os efeitos da entrada sejam desprezíveis, determine a vazão do óleo através do funil e calcule a "eficácia do funil", que pode ser definida como a razão entre a vazão real através do funil e a vazão máxima para o caso "sem atrito".

Tomamos o ponto 1 na superfície livre do óleo no reservatório cilíndrico e o ponto 2 na saída do funil, que também é considerado como nível de referência (). O fluido em ambos os pontos é aberto para a atmosfera (e, portanto, ) e que a velocidade do fluido na superfície livre é insignificante (). Para o caso ideal de “fluxo sem atrito”, a saída

velocidade é determinada a partir da equação de Bernoulli como:

Substituindo os valores, temos que:

Essa é a velocidade do fluxo para o caso sem atrito e, portanto, é o fluxo máximo velocidade. Em seguida, a vazão máxima e o número de Reynolds se tornam:

E

Então, o é menor que 2300. Portanto, o fluxo é laminar, como postulado. (Observe que, no caso real, a velocidade e, portanto, a O número de Reynolds será ainda menor, verificando se o fluxo é sempre laminar). O comprimento da entrada neste caso é:

Que é muito menor que o comprimento do tubo de 0,25 m. Portanto, os efeitos de entrada podem ser negligenciados como postulados. Observando que o fluxo através do tubo é laminar e pode ser assumido como totalmente desenvolvido, a taxa de fluxo pode ser determinada a partir da relação apropriada com , uma vez que o fluxo é descendente na direção vertical, então lembrando da fórmula da vazão em volume no escoamento laminar em um tubo horizontal:

Onde é a diferença de pressão no tubo, o .

Assim, substituindo os termos:

Então a "eficácia do funil" se torna: