Repita o Problema para uma entrada em aresta viva no tubo com . Essa "perda menor" é verdadeiramente "menor" ou não?

Desprezando as perdas menores, podemos utilizar a equação de energia (que é a de Bernoulli, com alguns acréscimos). Assim, estabelecendo os pontos de análise e , temos:

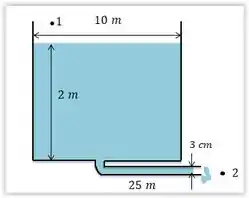
Pelo diagrama, os pontos e são expostos a atmosfera, ou seja, . Além disso, o nosso ponto de referência é em e a velocidade no ponto é desprezível, ou seja, . Por ultimo, não temos bomba nem turbina, então e . Assim, temos:

Como , então:

Isolamos a velocidade de saída:

Calculando, temos:

Assim, podemos calcular a vazão de descarga:

Para acharmos o tempo que a piscina esvazia completamente, podemos expressar a quantidade de água saindo durante um instante de tempo através da derivação:

Sendo que , logo

A massa que sai é igual a que está dentro do tanque, pelo fato de esvaziar, ocorre uma diminuição de nível:

Igualando as expressões e substituindo as variáveis, temos:

Isolando :

Vamos resolver nossa integral. Para isso, vale lembrar que o intervalo de tempo é e a altura , logo:

Substituindo os dados, temos:

Ou seja, essa diferença é de mais ou menos:

A perda é realmente menor!

Prontinho!!