Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 64

No Problema 9-20 desenvolvemos expressões para u , v   e ρ para escoamento através de um túnel de vento de alta velocidade. Encontre uma expressão para a função corrente compressível ψ p que descreva esse campo de escoamento. Por consistência, faça ψ p = 0 ao longo do eixo x. Desenhe o gráfico de várias linhas de corrente e verifique se elas coincidem com aquelas que você desenhou no Problema 9-20. Qual é o valor de ψ p na base superior do duto divergente?

Passo 1

Fala aí, tudo bem? Vem comigo que eu vou te ajudar a interpretar o enunciado e resolver esse problema.

Nessa questão, a gente tem que encontrar uma expressão pra ψ p baseada nas expressões de u , v   e ρ para um duto compressível convergente dadas no Problema 9-20. Vamos utilizar essa expressão pra traçar um gráfico da altura y do duto pela distância x no duto.

Além disso, temos que calcular o valor de ψ p para a base superior do duto dada pelo Problema 9-20, que é uma altura de y = 0,8   m .

Pra isso, a gente precisa definir a função corrente compressível (em coordenadas cartesianas) a partir das expressões:

ρ u = ∂ ψ p ∂ y   e   ρ v = - ∂ ψ p ∂ x

Indo no Problema 9-20, a gente encontra as seguintes expressões pras propriedades que vamos utilizar:

u =   u 1 + C u x

ρ =   ρ 1 + C p x

ρ v =   - ρ 1 C u + u 1 C p y - 2 C u C p x y

Mas espera um pouco! Antes de ir aos próximos passos, a gente tem que ir novamente ao Problema 9-20 e encontrar os valores de algumas das propriedades que vamos utilizar na resolução:

u 1 = 300 m s ρ 1 = 0,85 k g m 3   C u = - 100   s - 1 C p = 0,175 k g m 4

Então vem comigo que eu vou te ajudar a matar essa questão!

Passo 2

Primeiro, temos que escolher uma das equações que definem ψ p . Não importa a que a gente escolha, porque o resultado final é o mesmo. Por isso, vamos escolher ∂ ψ p / ∂ y .

Sendo assim:

∂ ψ p ∂ y = ρ u = ρ 1 + C p x u 1 + C u x = ρ 1 u 1 + u 1 C p + ρ 1 C u x + C p C u x ²

Agora, a gente vai integrar os dois lados da equação. Vamo lembrar que essa é uma integração parcial em y , pra qual   x é uma constante. Então, nossa constante de integração vai depender de x . Logo, a gente obtém:

ψ p =   ρ 1 u 1 y + u 1 C p + ρ 1 C u x y + C p C u x 2 y + g x

Agora, a gente deriva ψ p parcialmente em relação a x :

∂ ψ p ∂ x = ∂ ρ 1 u 1 y + u 1 C p + ρ 1 C u x y + C p C u x 2 y + g ( x ) ∂ x

→ ∂ ψ p ∂ x = u 1 C p + ρ 1 C u y + 2 C p C u x y + g ' ( x )

Então, a gente pega a expressão pra ∂ ψ p / ∂ x e a expressão pra ρ v que definimos lá em cima e iguala à essa expressão que acabamos de encontrar:

∂ ψ p ∂ x = - ρ v → u 1 C p + ρ 1 C u y + 2 C p C u x y + g ' x = ρ 1 C u + u 1 C p y + 2 C u C p x y

Se a gente olhar os dois lados da equação e compará-los, a gente percebe que:

g ' x = 0

Daí, basta a gente integrar em x e perceber que:

g x = C

Com C sendo uma constante qualquer.

Até agora, nossa expressão pra ψ p tá assim:

ψ p =   ρ 1 u 1 y + u 1 C p + ρ 1 C u x y + C p C u x 2 y + C

Lembre que nosso enunciado diz que, ao longo do eixo x (ou seja, y   =   0 ), vamos ter ψ p = 0 .

Se a gente substituir esses valores na equação lá em cima, vamos ter:

0 =   ρ 1 u 1 0 + u 1 C p + ρ 1 C u x 0 + C p C u x 2 0 + C

→ C = 0

Logo, a expressão pra ψ p pode ser escrita como:

ψ p =   ρ 1 u 1 y + u 1 C p + ρ 1 C u x y + C p C u x 2 y

Passo 3

Agora, precisamos montar uma expressão para y em função de x a partir da equação que definimos no passo anterior. Sendo assim, se colocarmos y em evidência e o isolarmos:

y ρ 1 u 1 + u 1 C p + ρ 1 C u x + C p C u x 2 =   ψ p

→ y = ψ p ρ 1 u 1 + u 1 C p + ρ 1 C u x + C p C u x 2

Se substituirmos os valores das propriedades que eu te mostrei no Passo 1, teremos:

y = ψ p 0,85 ( 300 ) + 300 0,175 + 0,85 - 100 x + 0,175 - 100 x 2

→ y ( x ) = ψ p 255 - 32,5 x - 17,5 x 2

Agora vamos plotar um gráfico a partir dessa expressão, variando ψ p como 0, 50, 100, 150 e 200. Utilizamos aqui o site Desmos. O gráfico, com as linhas de corrente para cada valor de ψ p , estão expostas abaixo:

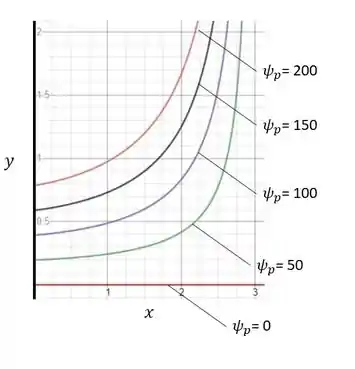
Passo 4

Pra gente finalizar a questão, vamos calcular agora é o valor de ψ p na base superior do duto divergente, que segundo o Problema 9-20 corresponde ao valor de y = 0,8   m e x = 0 .

Vamos, então, substituir esses valores na expressão que definimos no Passo 2:

ψ p , t o p o =   ρ 1 u 1 y + u 1 C p + ρ 1 C u 0 y + C p C u 0 2 y

→ ψ p , t o p o =   ρ 1 u 1 y = 0,85 k g m 3 300 m s 0,8   m

→ ψ p , t o p o = 204 k g m . s

Pronto, matamos o problema juntos!

Resposta

A linha de corrente compressível na parte superior do túnel de vento de alta velocidade é ψ p , t o p o = 204 k g m . s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere três fontes de igual intensidade m em uma configuração triangular: uma em (a/2, 0), uma em (-a/2, 0) e uma em (0, a). Trace as linhas de corrente desse escoamento. Existe algum ponto de esta
Quando um par fonte-sumidouro com m = 2 m²/s se combina com uma corrente uniforme, ele forma uma oval de Rankine cuja menor dimensão é 40 cm. Se a = 15 cm, quais são a velocidade da corrente e a veloc
Uma oval de Rankine de 2 m de comprimento e 1 m de altura é imersa em uma correnteU ∞ =10m / s , como na Figura P8.37. Avalie (a) a velocidade no ponto A e (b) a localização do ponto B onde uma partíc
Para que valor de K / ( U ∞a ) a velocidade no ombro de uma oval de Kelvin será igual a 4 U ∞ ? Qual é a altura h/a dessa oval?
Um cilindro circular é equipado com dois sensores de pressão de superfície para medir p a em θ =180 oep b em θ =105 o . A intenção é usar o cilindro como um anemômetro. Usando a teoria não viscosa, de