Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 140

Querosene a 20°C escoa a 18 m³/h em um tubo de 5 cm de diâmetro. Se for instalado um medidor do tipo placa de orifício de 2 cm de diâmetro, com tomadas de pressão de canto, qual será a queda de pressão medida em Pa?

Passo 1

E ai, galera! Tranquilidade? Bora que bora encarar mais um desafio?

Para o fluido dado, suas propriedades são:

ρ = 804   k g / m ³

μ = 1,9   x   10 - 3 k g m . s

Bem, a razão de aspecto do orifício é calculada como sendo a razão entre o diâmetro do orifício e o diâmetro do tubo:

β = 2 5 = 0,4

Passo 2

A velocidade poderá ser calculada dentro do tubo, uma vez que conhecemos a vazão do mesmo e também seu diâmetro.

V = Q A = 4 Q π D 2 = 4 18 3600 π 4 0,05 2 = 2 ,   55   m / s

Ali na vazão eu dividi por 3600 pra ela ficar em m³/s, beleza?

Com essa velocidade calculamos o valor de Reynold que é:

R e = ρ V D μ = 804 2,55 0,05 1,9   x   10 - 3 = 53300

Podemos então através da equação abaixo estimar qual será o valor de C d .

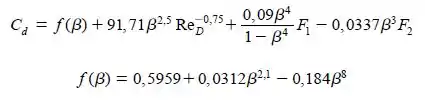
Bem, mas quem são esses F1 e F2, eles são parâmetros que tem valores de acordo com o tipo de tomada que estamos tendo. Por exemplo, no nosso caso são tomadas de canto, então eles possuem valores nulos.

C d = 0,5959 + 0,0312 0,4 2,1 - 0,184 0,4 8 + 91,71 0,4 2,5 53300 - 0,75 = 0,603

Passo 3

Temos uma equação que nos dá qual é a relação entre a vazão volumétrica do orifício e a queda de pressão:

Q = C d A 2 Δ p ρ 1 - β 4

18 3600 = 0,603 π 4 0,02 2 2 Δ p 804 1 - 0,4 4 → Δ p = 273   k P a

Resposta

Δ p = 273   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na instalação são dados: reservatório de grandes dimensões; f = 0,01 ; k s 2 = 2 ; γ = 10 4N / m 3 ; g = 10m / s 2 .Determinar:a) a vazão em volume;b) a perda de carga na instalação;c) o valor de x;d)
Construiu-se um viscosímetro tipo Saybolt que deverá ser calibrado por intermédio da medida da viscosidade de dois líquidos de viscosidade conhecida. Um dos líquidos, de viscosidade 0,46 St, escoa um
Sendo C v = 0,9 e C c = 0,6 , determinar a pressão p 1 , sabendo que o fluido é água e que sobe 3 m no tubo de Pitot. Determinar a vazão, sabendo que a área do orifício é 50 cm².
Qual é a diferença de pressão entre a seção maior e a garganta de um Venturi? A seção maior tem um diâmetro de 15 cm, e a garganta, de 7,5 cm. A vazão é 5 L/s de água. ( γ = 10 4N / m 3 ) Dado: C D =
Um pequeno objeto pesa 6 N no ar e 4,6 N quando mergulhado num líquido. O volume do objeto é 170 cm³. Qual é a massa específica, o peso específico e o peso específico relativo do líquido, se o peso es