Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 20

A Segunda Lei de Newton é a base da equação diferencial de conservação do momento linear (a ser discutida no Capítulo 9). Em termos da aceleração material acompanhando uma partícula de fluido (Figura P7-19), nós escrevemos a Segunda Lei de Newton da seguinte maneira:

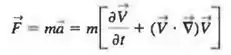
Ou então, dividindo ambos os lados pela massa m da partícula de fluido,

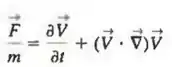
Escreva as dimensões primárias de cada termo aditivo da equação e certifique-se de que a equação seja dimensionalmente homogênea. Mostre todo o seu trabalho.

Passo 1

Oi pessoal, tudo bem?

As dimensões primárias da derivada do tempo ( ∂ / ∂ t ) são 1 / t e m p o . As dimensões primárias do gradiente o vetor tem 1 / c o m p r i m e n t o e as dimensões primárias da velocidade são o c o m p r i m e n t o / t e m p o .

Em resumo, somente relembramos as dimensões primárias de cada termo. Vamos agora ver se a equação é dimensionalmente homogênea.

Passo 2

Bem, relembrando, a equação é:

F m → =   ∂ V → ∂ t + ( V → ⋅ ∇ → ) V →    

Assim, cada termo na equação pode ser escrito em termos de dimensões primárias:

F m → = m a s s a ⋅ a c e l e r a ç ã o m a s s a = a c e l e r a ç ã o = m s 2   o u c o m p r i m e n t o t e m p o 2   ;

∂ V → ∂ t = m e t r o s e g u n d o ⋅ 1 s e g u n d o = m s 2   o u c o m p r i m e n t o t e m p o 2   ;  

V → ⋅ ∇ → V → = m e t r o s e g u n d o ⋅ 1 m e t r o m e t r o s e g u n d o = m s 2   o u c o m p r i m e n t o t e m p o 2

Resposta

Portanto, foi provado que a equação é dimensionalmente homogênea.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Aeronautical engineers measure the pitching moment M0of a wing and then write it in the following form for use inother cases:M0 5 βV2 AC ρwhere V is the wing velocity, A the wing area, C the wingchord
In his study of the circular hydraulic jump formed by afaucet flowing into a sink, Watson [53] proposed a parameter combining volume flow rate Q, density ρ, and viscosity µ of the fl uid, and depth h
The height H that fluid rises in a liquid barometer tubedepends upon the liquid density ρ, the barometric pressurep, and the acceleration of gravity g. (a) Arrange these fourvariables into a single di
In English Engineering units, the specifi c heat cp of air atroom temperature is approximately 0.24 Btu/(lbm-8F).When working with kinetic energy relations, it is more appropriate to express cp as a v
Experimental data [55] for the density of n-pentane liquidfor high pressures, at 508C, are listed as follows:Pressure, kPa 100 10,230 20,700 34,310Density, kg/m3 586.3 604.1 617.8 632.8(a) Fit this da