Um átomo de hidrogênio é excitado de um estado com até um com . (a) Calcule a energia que deve ser absorvida pelo átomo. (b) Calcule e trace sobre um diagrama de níveis de energia as energias dos diferentes fótons que serão emitidos se o átomo voltar a seu estado . (c) Calcule a velocidade de recuo do átomo de hidrogênio, ao fazer uma transição de a em um único salto quântico, supondo que ele está inicialmente em repouso.
Passo 1
Fala galerinha, beleza?
A energia, em , do -ésimo estado do átomo de hidrogênio é dada por
Assim, para , temos
Para :
Portanto, a energia que deve ser absorvida pelo átomo é
Passo 2
A seguir reproduzimos todas as transições entre e passando por todas os níveis intermediários possíveis:
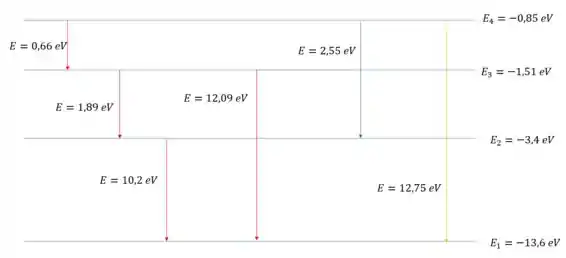
Passo 3
Vamos para o item (c)!
Vimos no item (a) que a energia liberada devido a transição eletrônica de até é
Essa energia vai ser dividida entre o fóton e o recuo do átomo. Portanto,
Substituindo as expressões das energias, obtemos
Agora vem a parte chave: pela conservação do momento, devemos ter
Em módulo, temos
Assim,
Precisamos resolver essa equação quadrática:
Como , devemos considerar apenas o sinal positivo da raiz:
Usando e , podemos usar a aproximação :
Usei a relação , se .
Assim,
Como , temos
Agora substituímos os números: