Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 7.Problemas - Ex. 15
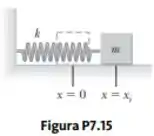
Um bloco de massa m = 2,00 kg é preso a uma mola com constante elástica , como mostrado na Figura P7.15. O bloco é puxado para uma posição cm para a direita do equilíbrio e solto do repouso. Encontre a velocidade que o bloco tem enquanto passa pelo equilíbrio se (a) a superfície horizontal não tem atrito e (b) o coeficiente de atrito entre bloco e superfície é .
Passo 1
Aqui então a gente vai avaliar o caso em duas situações: uma sem dissipação de energia, outra com dissipação de energia devida ao atrito.
(a)Aqui, considerando o princípio da conservação da energia, sem dissipação por atrito, a gente vê que a energia potencial elástica da mola vai se converter totalmente em energia cinética pro bloco.
Escrevendo isso matematicamente, a gente tem:
Dá pra gente simplificar os denominadores, né? Ficamos assim então:
Aplicando os dados do enunciado, a gente determina (cuidado com as unidades, todas no sistema internacional!):
Então, sem atrito, o bloco tem essa velocidade ao passar no ponto de repouso da mola!
Passo 2
(b)Agora, gente, considerando o atrito, uma parte da energia potencial elástica da mola, quando o bloco for liberado, vai ser transformada em calor, pelo atrito, em vez de se transformar 100% em energia cinética pro bloco, sacou?
Então, agora, gente reescreve a primeira expressãozinha do Passo 1 considerando o trabalho do atrito, , assim:
Matematicamente, a gente vai ter:
Onde , sendo e , respectivamente, a força de atrito e o deslocamento!
A gente sabe lá da dinâmica (leis de Newton) que , e que quando estamos avaliando o deslocamento de um corpo na horizontal, a força normal é equivalente à força peso, sendo assim , correto?
Então, reescrevemos nossa última equação assim:
Aqui, a gente quer também a velocidade, certo? Vamos isolar de todo mundo, fazendo ajustes matemáticos básicos!
Comecemos por multiplicar ambos os lados da igualdade por 2 e sumimos com os denominadores:
Agora, passamos pro outro lado, isolando :
E é isso, gente! Considerando , agora é só aplicar os dados que a gente tem, cuidando das unidades, ficando com o seguinte:
Repara que, agora, a velocidade é menor, já que houve perda de energia pelo atrito. Isso é bem razoável, já que, senão, o bloco teria mais velocidade, como a gente viu, sem atrito!
Resposta
(a)
(b)