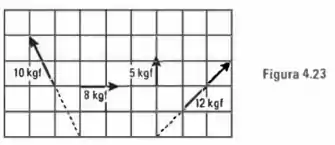
Calcule a intensidade e a posição da resultante das forças representadas na Fig. 4.23. O lado de cada quadrado é de .
Passo 1
E aí, beleza?? Primeiramente vamos calcular a força resultante do sistema:
Somando:
Passo 2
Essas forças são localizadas pelos vetores:
Portanto, o torque total é:
Somando:
Passo 3
Para descobrir o ponto de aplicação, fazemos:
Portanto:
Assim, os pontos de aplicação de são aqueles que possuem e estão sobre a reta:
Resposta
os pontos de aplicação de são aqueles que possuem e estão sobre a reta: