Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 10.1 - Ex. 75
Um corpo maciço de massa , colocado sobre uma superfície horizontal sem atrito, está preso a um fio que é enrolado em torno de um pilar cilíndrico vertical preso à superfície. Assim, quando o corpo é colocado em movimento, ele segue uma trajetória que espirala para dentro. (a) A quantidade de movimento angular do corpo, em relação ao eixo do pilar, é conservada? Explique sua resposta. (b) A energia do corpo é conservada? Explique sua resposta. (c) Se a rapidez do corpo é , quando o comprimento da parte desenrolada do fio é , qual é a rapidez quando o comprimento da parte desenrolada do fio foi encurtado para ?
Passo 1
Então, galera, o que a gente tem que entender aqui é o seguinte:
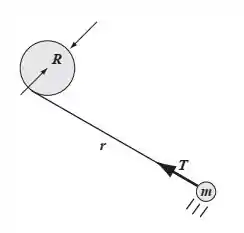
O objeto está amarrado nesse fio, que por sua vez está amarrado em um poste. Conforme ele vai se aproximando do poste, o fio vai se enrolando e diminuindo de tamanho. Então a gente tem que fazer o seguinte: vamos relacionar o torque à variação da quantidade de movimento angular. Se houver torque, houve variação da quantidade de movimento, e então o momento angular não se conserva. Bora lá!
Passo 2
- O torque que age no objeto é calculado como:
- Vamos ter que reparar algumas coisas:
- Como a gente viu no item (b), a energia se conserva. Então, aplicando conservação da energia para o corpo, vamos obter:
Mas o torque é igual à variação na quantidade de movimento angular:
Então tá vendo que houve variação de quantidade de movimento angular, que foi igual a ? Sendo assim, o momento angular não se conserva!
Passo 3
Primeiro, a velocidade e a tração são perpendiculares! Dá uma olhada lá no desenho pra reparar isso. Mas o deslocamento do corpo é na direção da velocidade, então o deslocamento também é perpendicular à força a todo momento. Lembra que o trabalho é função da força e do deslocamento?
Isso é tipo um produto escalar da força com o . Como a força é perpendicular ao , esse produto escalar vai dar . Então não tem trabalho!
O que poderia fazer com que a energia não se conservasse? Só se um trabalho externo atuasse, né? Mas a gente viu que o trabalho que poderia haver nesse caso é nulo. Então, a energia não vai ter nada que a modifique, e assim podemos dizer que há conservação de energia!
Passo 4
O momento de inércia do cilindro é igual a . Podemos usar também a condição de não deslizamento, .
Agora é só a gente dar uma arrumada nessa brincadeira aí. Cortando o que a gente tem que cortar, vamos chegar em:
Resposta
Ei, a resposta está no passo a passo :)