Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 13.Exercícios e Problemas - Ex. 26

26. Duas esferas de chumbo de cada uma são suspensas por cabos de massa desprezível com de comprimento cada um. As extremidades superiores dos cabos foram cuidadosamente ancoradas a exatamente de distância uma da outra. Qual é a distância entre os centros das esferas?

Passo 1

Então, de rápida impressão podemos achar que a distância entra as bolas vai ser já que os cabos que elas estão presas estão separados por essa distância.

Mas não é bem assim que acontece já que existe uma força gravitacional entre as esferas logo elas se deslocam uma em direção a outra, fazendo um ângulo com a vertical.

Abaixo podemos ver um diagrama de corpo livre para essa situação mostrando as forças que estão atuando nas esferas.

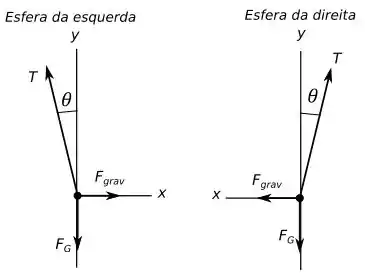
Pensando dessa forma cada esfera teve um deslocamento de uma na direção da outra por conta da força gravitacional, então temos que a distância entre elas é dada por:

Então temos que dar um jeito de encontrarmos um valor para .

Para achar esse ângulo vamos usar uma velha conhecida nossa, a segunda lei de Newton. Como as esferas estão em repouso temos que a força resultante tanto na direção quanto na direção é zero.

Vamos atrás desse .

Passo 2

Para esse problema basta analisar uma das esferas já que elas são idênticas e sofrem das mesmas forças. Vamos analisar a da esquerda.

Na direção , temos:

Na direção temos o seguinte:

Passo 3

Abem, no passo anterior encontramos uma expressão para e uma para o , vamos dividir um pelo outro, já que:

Então temos o seguinte:

Agora vamos usar o fato de que a força gravitacional entre as esferas é dada por:

Com isso temos que:

Então galera sabemos todos os valores de forma tranquila menos que é o que queremos, por isso vamos fazer uma aproximação, sabemos que terá um valor muito próximo de , já que a força não será muito grande por conta das esferas não serem muito grandes.