Exercícios de Força e Campo Gravitacional - Lista de Exercícios Resolvida
Questão 1
Na superfície da Lua, a aceleração da gravidade vale . A uma distância do centro da Lua igual a quatro vezes o raio da Lua, a aceleração da gravidade vale:
- Nenhuma dessas respostas
Questão 2
Duas esferas uniforme, cada uma com massa e raio , estão em contato. Qual é o módulo da força de atração gravitacional entre elas?
Ver solução completaQuestão 3
Uma esfera de chumbo de raio possui uma cavidade esférica cuja superfície passa pelo centro da esfera e “toca” o lado direito da esfera. A massa da esfera, antes de a cavidade ser aberta, era . Com que força gravitacional a esfera de chumbo com a cavidade atrai uma pequena esfera de massa que se encontra a uma distância do centro da esfera de chumbo, sobre a reta que liga os centros da esfera e da cavidade?
.
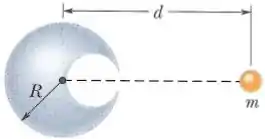
Questão 4
Duas esferas uniformes, cada uma com massa igual a , estão fixas nos pontos e . Determine o módulo, a direção e o sentido da aceleração inicial de uma esfera uniforme com massa quando ela é liberada do repouso no ponto e sofrendo apenas atrações gravitacionais das esferas situadas em e .
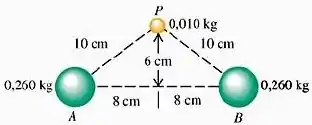
Questão 5
Duas partículas, cada uma de massa , separadas por uma distância interagem com força gravitacional de módulo . Duas outras partículas, cada uma de massa , separadas por uma distância interagem com força gravitacional de módulo
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 6
Uma partícula pontual de massa está sobre o eixo em e uma partícula idêntica está sobre o eixo em . (a) Qual é a orientação do campo gravitacional da origem? (b) Qual é a magnitude deste campo?
Ver solução completaQuestão 7
Sabendo que a aceleração da gravidade na superfície da Terra é igual a , desprezando o efeito da latitude, qual deve ser a altura acima da superfície terrestre na qual a aceleração da gravidade é igual a ?
Ver solução completaQuestão 8
Cinco corpos, cada um de massa , estão igualmente espaçados sobre um arco de semicírculo de raio , como na Figura 11-25. Um corpo de massa está localizado no centro de curvatura do arco. (a) Se é , é e é , qual é a força gravitacional sobre a partícula de massa devida aos cinco corpos? (b) Se o corpo de massa é removido, qual é o campo gravitacional no centro de curvatura do arco?
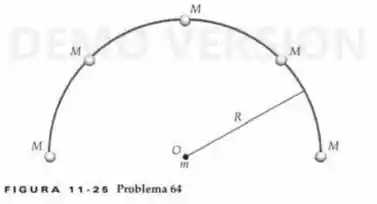
Questão 9
Você foi contratado por uma agência espacial para estudar sobre um novo planeta recém descoberto, e sua primeira função é calcular a gravidade na superfície do planeta. Já é conhecida sua massa de e seu raio de . De acordo com seus cálculos, qual é o valor da gravidade em questão?
Dado:
Ver solução completaQuestão 10
Um planeta tem massa quatro vezes maior do que a da Terra, mas a aceleração da gravidade em sua superfície é a mesma que na superfície da Terra. O raio do planeta é:
Questão 11
Comparado com o seu peso na superfície da Terra, o seu peso na superfície de um planeta que tem quatro vezes a massa da Terra e o dobro do raio da Terra seria
(A) o triplo do seu peso na Terra.
(B) o dobro de seu peso na Terra.
(C) a metade de seu peso na Terra.
(D) quatro vezes o seu peso na Terra.
(E) igual ao seu peso na Terra.
Ver solução completaQuestão 12
Quatro partículas, cada uma de massa , estão sobre o eixo- simetricamente alinhadas em relação à origem. Uma quinta partícula de massa está localizada sobre o eixo-. A direção da força gravitacional exercida sobre a partícula de massa M é
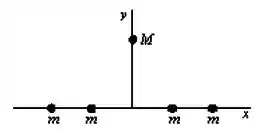
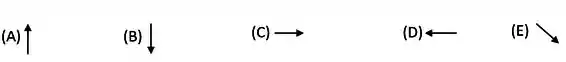
Questão 15
No instante de máxima aproximação, um satélite da Terra passa com velocidade igual a a uma distância de do centro da Terra. Nesse instante, o módulo da aceleração do satélite é:
- Nenhuma das respostas anteriores
Questão 16
Um satélite move-se inicialmente em uma órbita circular de raio em torno da Terra. Se ele se mover em uma órbita de raio , a força gravitacional exercida sobre o satélite se tornará:
(a) do valor inicial
(b) do valor inicial
(c) do valor inicial
(d) vezes o valor inicial
(e) vezes o valor inicial
Ver solução completaQuestão 17
Dois satélites são colocados em órbitas geossíncronas, que são órbitas com um período de 24 horas nas quais cada satélite paira sobre um ponto acima do equador da Terra. O satélite B tem três vezes a massa do satélite A. Qual é a relação entre as magnitudes das forças gravitacionais da Terra nos dois satélites?
a) FB = 1/9 FA
b) FB= 1/3 FA
c) FB = FA
d) FB = 3 FA
e) FB = 9 FA
Ver solução completaQuestão 18
A figura mostra quatro arranjos de três partículas de massas iguais. Ordene os arranjos de acordo com o módulo da força gravitacional resultante sobre a partícula identificada por , começando pela maior
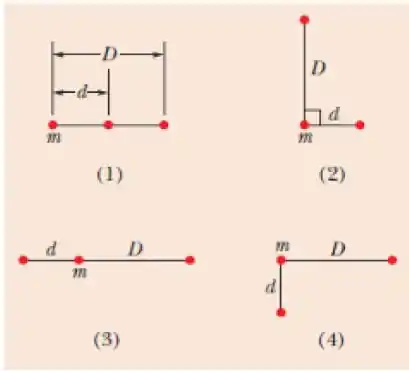
(a) 1, depois 2 e 4 empatados, 3
(b) 1, 2, 3, 4
(c) 1 e 2 empatados, 3, 4
(d) 2 e 4 empatados, 1, 3
(e) 4, 3, 2, 1
Ver solução completaQuestão 19
Como sabemos, Garfield é um gato preguiçoso. Se ele levar uma caixa com suprimento de lasanha da Terra à Lua podemos afirmar que o esforço que ele fará para carregar a caixa na Lua será:
- Menor que na Terra, já que a massa da caixa permancerá constante e seu peso diminuirá
- Menor que na Terra, já que a massa da caixa diminuirá e seu peso permanecerá constante
- Menor que na Terra, já que a massa da caixa aumentará e seu peso diminuirá
- Maior que na Terra, já que a massa da caixa permancerá constante e a seu peso aumentará
- Maior que na Terra, já que a massa da caixa diminuirá e seu peso aumentará
Questão 20
Uma esfera de chumbo de raio possui uma cavidade esférica cuja superfície passa pelo centro da esfera e “toca” o lado direito da esfera. A massa da esfera, antes de a cavidade ser aberta, era . Com que força gravitacional a esfera de chumbo com a cavidade atrai uma pequena esfera de massa que se encontra a uma distância do centro da esfera de chumbo, sobre a reta que liga os centros da esfera e da cavidade?
.
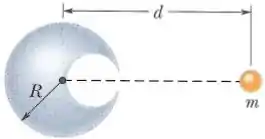
Questão 21
Em um sistema binário consistindo de duas estrelas de mesma massa, onde a energia potencial gravitacional é igual a zero?
- em um ponto infinitamente afastado das estrelas;
- em nenhum ponto;
- exatamente a meio caminho entre as estrelas;
- em um ponto bem próximo de uma delas;
- ao longo da mediatriz da reta ligando as estrelas;
Questão 22
Um planeta de massa está em órbita em torno de outro planeta muito maior, de massa . A distância média entre os planetas é e a única força presente é a força gravitacional, , que é de atração. Em um ciclo (volta), o planeta volta à mesma configuração inicial. Qual é o trabalho feito sobre o planeta de massa m durante um ciclo (volta)?
a)
b)
c)
d)
e)
Ver solução completaQuestão 23
Um objeto é abandonado do repouso de uma altitude acima da superfície da Terra. Se é a massa da Terra e é o seu raio, a velocidade do objeto imediatamente antes de atingir a superfície da Terra é
Questão 24
A figura mostra três arranjos das mesmas partículas idênticas, com três delas colocadas sobre um arco de circunferência de raio , e a quarta colocada no centro do arco. Ordene os arranjos de acordo com o módulo da força gravitacional resultante que age sobre a partícula central devido às outras três partículas, começando pela maior.
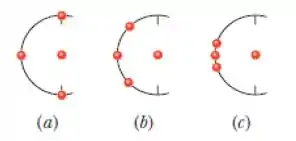
(a) c, b, a;
(b) c, a, b;
(c) b, c, a;
(d) b, a, c;
(e) c, depois a e b empatados;
Ver solução completaQuestão 25
A figura ao lado mostra duas partículas puntiformes, A e B, fixadas espacialmente e separadas por uma distância d. A partícula A possui massa e a partícula B possui massa . Uma terceira partícula puntiforme deve ser colocada entre A e B. Qual o valor da distância x de modo que a partícula C esteja em equilíbrio estático apenas sob a ação das forças gravitacionais de A e B?
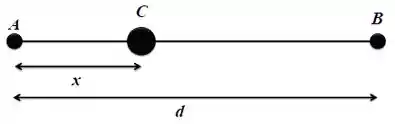
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
Ver solução completaQuestão 26
Se um objeto na superfície da Terra tem peso P, qual seria o peso do objeto na superfície de um planeta com um sexto da massa da Terra e um terço do raio da Terra?
a) P;
b) P/3;
c) 3P;
d) 4P/3;
e) 3P/2;
Ver solução completaQuestão 27
(D) A atração gravitacional entre você e o Sol é maior ao meio-dia ou à meia-noite? Explique.
Ver solução completaQuestão 28
Sabendo que a aceleração da gravidade na superfície da Terra é igual a , desprezando o efeito da latitude, qual deve ser altura acima da superfície terrestre na qual a aceleração da gravidade é igual a ?
Dados:
Constante gravitacional:
Massa da Terra:
Ver solução completaQuestão 29
Uma massa pontual de e outra de são mantidas fixas a de distância. Uma partícula de massa é solta de um ponto entre as duas massas a da massa de ao longo da linha que une as duas massas fixas. Qual o módulo, a direção e o sentido da aceleração da partícula imediatamente após ser solta?
Dados:
Ver solução completaQuestão 30
Na figura abaixo, a partícula é mantida fixa em no eixo e a patícula , com uma massa de é mantida na origem. Uma partícula (não mostrada) pode ser deslocada ao longo do eixo , entre a partícula e . A figura mostra o gráfico da força gravitacional resultante exercida pelas partículas e sobre a partícula em função da posição da partícula . O gráfico, na verdade, se estende indefinidamente para a direita tendendo assintoticamente para para . Qual é a massa da partícula e da partícula ?
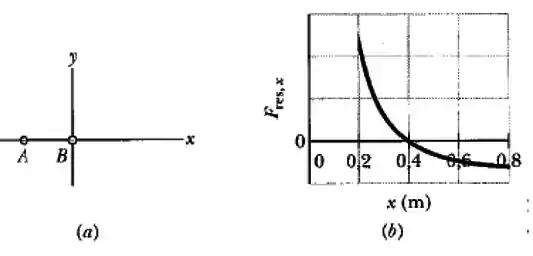
Considere as massas pontuais e a constante gravitacional .
(a) ,
(b) ,
(c) ,
(d) ,
(e) ,
(f) ,
Ver solução completaQuestão 32
Imagine o sistema composto pelo planeta Terra de massa e pela Lua com massa . Seja ainda a distância entre a Terra e a Lua dada por . A que distância da Terra sobre a reta que une os dois corpos a força gravitacional sobre uma partícula ali situada será zero?
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 33
Uma massa uniformemente distribuída em uma esfera maciça de raio e centro na origem exerce sobre uma partícula de massa a uma distância da origem uma força de módulo Determine o valor da razão nos seguintes casos:
- e
- e
Questão 34
Duas partículas, cada uma de massa , separadas por uma distância interagem com força gravitacional de módulo . Duas outras partículas, cada uma de massa , separadas por uma distância interagem com força gravitacional de módulo:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 35
A magnitude da aceleração de um planeta em órbita em torno do Sol é proporcional
(A) À massa do planeta.
(B) Ao quadrado da distância entre o planeta e o Sol.
(C) À distância entre o planeta e o Sol.
(D) Ao inverso da distância entre o planeta e o Sol.
(E) À massa do Sol.
Ver solução completaQuestão 39
O Princípio da Equivalência afirma que:
- A massa do planeta pode ser considerada como concentrada em seu centro.
- Que o modelo heliocêntrico de Copérnico equivale ao modelo geocêntrico de Ptolomeu.
- Que as órbitas dos planetas correspondem a elipses com o Sol situado num dos seus focos.
- Que apesar de conceitualmente diferentes, as massas inercial e gravitacional são iguais.
- Que a aceleração e a constante de gravitação universal não se equivalem.
Questão 40
A que distância de uma esfera de e raio uma partícula teria de ser posta para que a esfera atraísse a partícula com a mesma força com que a Terra atrai esta partícula posta na sua superfície? Esse experimento poderia ser efetivamente realizado?
Dados:
Raio da Terra:
Massa da Terra:
Ver solução completaQuestão 41
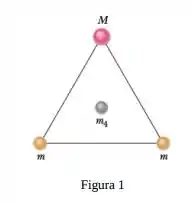
Como mostra a figura , duas esferas de massa e uma terceira esfera de massa formam um triângulo equilátero e uma quarta esfera de massa ocupa o centro do triângulo. A força gravitacional sobre a esfera central é nula.
Qual é o valor de em termos de ?
Questão 42
Três estrelas, cada uma com a massa do Sol, formam um triângulo equilátero com lados de . (Este triângulo se encaixaria com precisão da órbita de Júpiter). O triângulo precisa girar, pois do contrário, as estrelas colidiram no centro. Qual é o período de rotação? Expresse sua resposta em anos.
Ver solução completaQuestão 43
Acredita-se que alguma estrelas de nêutrons (estrelas extremamente densas) estão girando a cerca de . Se uma dessas estrelas têm um raio de , qual deve ser, no mínimo, a sua massa para que uma partícula na superfície da estrela permaneça no lugar apesar da rotação?
Ver solução completaQuestão 44
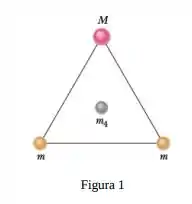
Como mostra a figura , duas esferas de massa e uma terceira esfera de massa formam um triângulo equilátero e uma quarta esfera de massa ocupa o centro do triângulo. A força gravitacional sobre a esfera central é nula.
Se dobrarmos o valor de , qual será o novo módulo da força gravitacional a que está submetida a esfera central?
Questão 45
A figura mostra uma cavidade esférica no interior de uma esfera de chumbo de raio ; a superfície da cavidade passa pelo centro da esfera e “toca” o lado direito da esfera. A massa da esfera antes de ser criada a cavidade era . Com que força gravitacional a esfera de chumbo com a cavidade atrai uma pequena esfera de massa que se encontra a uma distância do centro da esfera de chumbo, sobre a reta que liga os centros das esferas e o centro da cavidade?
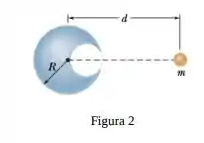
Questão 46
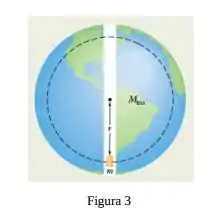
Suponha que um planeta é uma esfera homogênea de raio que (de alguma forma) possui um túnel radial estreito que passa pelo centro do planeta (figura 3). Suponha também que é possível posicionar uma maçã em qualquer lugar do túnel ou do lado de fora do planeta. Seja o módulo da força gravitacional experimentada pela maçã quando está na superfície do planeta. A que distância da superfície está o ponto no qual o módulo da força gravitacional que o planeta exerce sobre a maçã é se a maçã for deslocada:
Para longe do planeta?
Questão 47
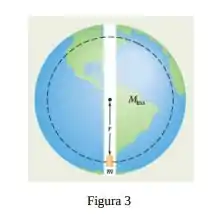
Suponha que um planeta é uma esfera homogênea de raio que (de alguma forma) possui um túnel radial estreito que passa pelo centro do planeta (figura 3). Suponha também que é possível posicionar uma maçã em qualquer lugar do túnel ou do lado de fora do planeta. Seja o módulo da força gravitacional experimentada pela maçã quando está na superfície do planeta. A que distância da superfície está o ponto no qual o módulo da força gravitacional que o planeta exerce sobre a maçã é se a maçã for deslocada:
Para dentro do túnel?
Questão 48
Estrelas de nêutrons possuem aproximadamente a mesma massa que o Sol, porém um diâmetro muito menor do que o deste. Considere uma pessoa cujo peso na Terra seja . Que massa um objeto deve ter para que seu peso na Terra seja igual ao peso da pessoa na superfície de uma estrela de nêutrons?
Considere uma estrela de nêutrons com a mesma massa do sol e um diâmetro de 20,0 km.
Dados:
Massa do sol:
Constante gravitacional:
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 49
Qual é o módulo e qual é a direção da força gravitacional resultante sobre a massa de da figura ?
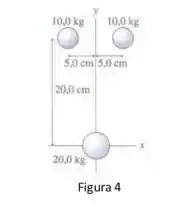
Questão 50
Suponha que a Terra de repente parasse de girar em torno do Sol. A força gravitacional a atrairia diretamente para o Sol. Qual seria a velocidade da Terra quando colidisse com ele?
Ver solução completaQuestão 51
Plutão se movimenta em uma órbita claramente elíptica em torno do Sol. A velocidade de Plutão em seu ponto mais próximo, do Sol é de . Qual é a velocidade de Plutão no ponto mais distante de sua órbita, onde se encontra a do Sol?
Ver solução completaQuestão 52
Um satélite está em órbita circular de raio em torno da Terra. A área delimitada pela órbita é proporcional a , já que . Determine a forma de variação com das seguintes propriedades do satélite:
A energia cinética;
Ver solução completaQuestão 53
Um satélite está em órbita circular de raio em torno da Terra. A área delimitada pela órbita é proporcional a , já que . Determine a forma de variação com das seguintes propriedades do satélite:
O momento angular;
Ver solução completaQuestão 54
Duas estrelas de nêutrons estão separadas por uma distância de . Ambas tem uma massa de e um raio de . As estrelas se encontram inicialmente em repouso relativo. Com que velocidade estarão se movendo, em relação a este referencial de repouso:
Quando a distância for metade do valor inicial?
Ver solução completaQuestão 55
Duas estrelas de nêutrons estão separadas por uma distância de . Ambas tem uma massa de e um raio de . As estrelas se encontram inicialmente em repouso relativo. Com que velocidade estarão se movendo, em relação a este referencial de repouso:
Quando estiverem na iminência de colidir?
Ver solução completaQuestão 56
Um satélite está em órbita circular de raio em torno da Terra. A área delimitada pela órbita é proporcional a , já que . Determine a forma de variação com das seguintes propriedades do satélite:
O período;
Ver solução completaQuestão 57
Um satélite está em órbita circular de raio em torno da Terra. A área delimitada pela órbita é proporcional a , já que . Determine a forma de variação com das seguintes propriedades do satélite:
A velocidade escalar.
Ver solução completaQuestão 58
Duas esferas homogêneas de são mantidas fixas nas posições cujas coordenadas são e . Determine: o módulo, a direção e sentido da força gravitacional resultante devida a essas esferas sobre uma terceira esfera homogênea de massa igual a , situada no ponto de coordenadas , . Represente os vetores força gravitacional em termos dos vetores unitários.
Ver solução completaQuestão 59
A figura ao lado mostra três esferas de massas localizadas nos vértices de um triângulo equilátero de lado . Uma quarta esfera de massa está localizada no centro do triângulo. Sabe-se que todas as esferas se mantêm fixas em suas posições. A constante de gravitação universal é dada por . Quando possível, expresse suas respostas em termos de , , e .
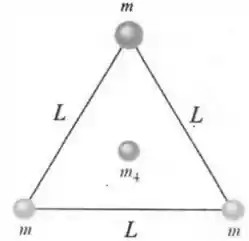
- Considerando que a energia potencial gravitacional é nula no infinito, calcule a energia potencial entre a esfera de massa localizada no vértice superior do triângulo e a massa central .
- Calcule o valor da força gravitacional resultante que as duas esferas de massa localizadas nos vértices inferiores do triângulo exercem sobre a esfera central de massa
- Determine o valor da força gravitacional resultante total a que a massa central estará submetida por sua interação com todas as três massas . Justifique sua resposta.
Questão 60
A magnitude da aceleração de um planeta em órbita em torno do Sol é diretamente proporcional
(A) à massa do planeta.
(B) à massa do Sol.
(C) à distância entre o planeta e o Sol.
(D) ao produto das massas do planeta e do Sol.
(E) ao quadrado da distância entre o planeta e o Sol.
Ver solução completaQuestão 61
A massa do Sol é aproximadamente vezes maior que a massa da Terra. A distância do Sol à Lua é aproximadamente vezes a distância da Terra à Lua. Qual a razão entre a força que o Sol faz sobre a Lua e a força que a Terra faz sobre a Lua?
Ver solução completaQuestão 64
O grupo musical "Os Paralamas do Sucesso", fez sucesso com a canção Tendo a Lua, em um dos trechos dessa música, o vocalista Herbert Vianna diz:
"Tendo a lua aquela gravidade aonde o homem flutua
Merecia a visita não de militares,
Mas de bailarinos
E de você e eu".
Ao escrever essa letra, o músico Herbert Vianna lembrou-se que na lua o homem flutua porque:
(a) Na Terra ou na Lua o corpo possui o mesmo peso, o músico Herbert Vianna está enganado.
(b) Na Lua a massa do corpo é seis vezes menor, por isso o corpo flutua.
(c) A massa e o peso do corpo não são diferentes nesses locais, apesar das gravidades serem diferentes. O autor Herbert Vianna cometeu um erro grave na letra dessa canção.
(d) Na Lua o peso do corpo é aproximadamente 6 vezes menor do que na Terra, por isso o corpo flutua.
(e) Na Terra a massa do corpo é cerca de 6 vezes menor do que na Lua.
Ver solução completa


