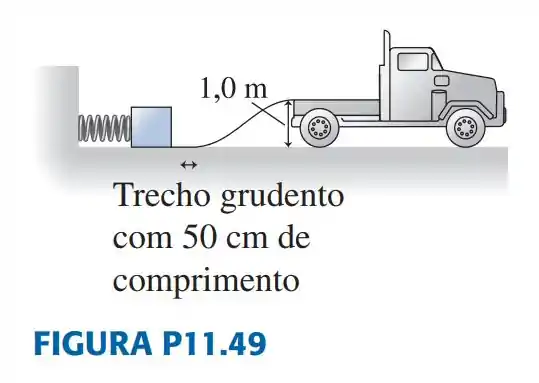
Uma empresa de fretes usa uma mola comprimida para lançar pacotes de para dentro de um caminhão usando uma rampa de de altura, como mostrado na FIGURA P11.49. A constante elástica da mola vale e a mola está comprimida em .
a. Qual é o valor da velocidade de um pacote quando ele chega à carroceria do caminhão?
b. Um funcionário descuidado derrama seu refrigerante sobre a rampa. Isso cria uma mancha grudenta de de comprimento com coeficiente de atrito cinético de . O próximo pacote arremessado chegará à carroceria do caminhão?
Passo 1
No início do sistema temos apenas a energia elástica da mola e no final temos a energia potencial gravitacional da caixa e a energia cinética da caixa, então:
Com sendo a energia cinética, a energia potencial gravitacional e a energia potencial elástica. Logo pela conservação da energia mecânica temos:
Então a velocidade da caixa será de:
Então aplicando os valores teremos:
Passo 2
Agora o estagiário foi lá e fez cagada e derramou DOLLY O SABOR BRASILEIRO na rampa, isso fez com que a nossa conservação de energia fosse alterada de modo que temos:
Então se for um número complexo então não teremos solução, calculando nessa situação nós teremos:
Pois considera-se essa distância como uma distância onde é normal ao plano. Substituindo os valores agora nós teremos:
Então o pacote não chega na carroceria. Ele quase chega mas não vai.